1.1 Hauptziele der Quantenmechanik

1.1 Hauptziele der Quantenmechanik

Frage 1: Welche Art von Anregungen k¨onnen Elektronen, Atome und Molek¨ule annehmen?
Frage 2: Wie berechnet man diese Energien (Energiequantelung)?
Frage 3: Wie berechnet man Strukturen und Bindungsverh¨altnisse sowie Eigenschaften von
Molek¨ulen aus grundlegenden Prinzipien?

Makroskopische Materie zeigt in der Regel keine diskreten Zustände. Mikroskopische Materie „benimmt“ sich aber anders. Wir wollen in den nächsten Kapiteln folgende Frage beantworten:

Wir wollen das Problem des harmonischen Oszillators klassisch lösen.

Zielsetzung:

Determinismus, das heißt Ort und Impuls (Bewegungszustand) jedes Objektes zu jedem Zeitpunkt berechenbar (aus bekannten Startpunkten und Kräften) Dies ist möglich durch Vorgabe des Impuls- und Energieerhaltungssatzes oder der Newtonschen Bewegungsgleichung.

Energieerhaltungssatz $Eges = Ekin + Epot$

$1 2 Eges = 2mv + V (x) f¨ur eindimensionalen Fall$

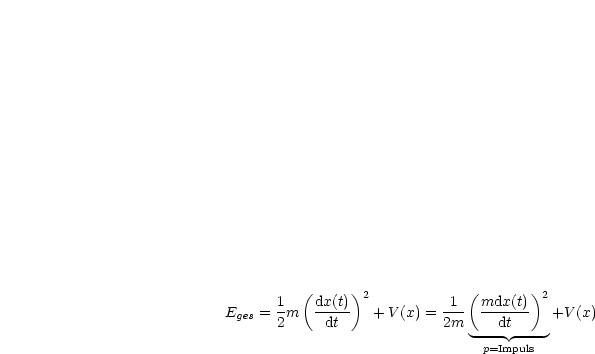
$( )2 ( )2 Eges = 1m dx(t) + V(x) =-1- mdx(t) +V (x) 2 dt 2m ---dt ---- p=Impuls$

$p2 Eges = ---+ V (x) 2m$
Newtonsche Bewegungsgleichungen $dV-(x)- F = ma = mx¨(t) = - dx$
Weiterhin gilt auch:
$( ) ( ) d2x(t) dv(t) dp(t)- F = m dt2 = m dt = dt$
Hieraus ergibt sich:
$|-------------| |˙p(t) = -dV-(x)| ----------dx---$

Beispiel:

Wir betrachten den klassischen harmonischen Oszillator, also die Bewegung einer Kugel unter dem Einfluß des Hookeschen Gesetzes.

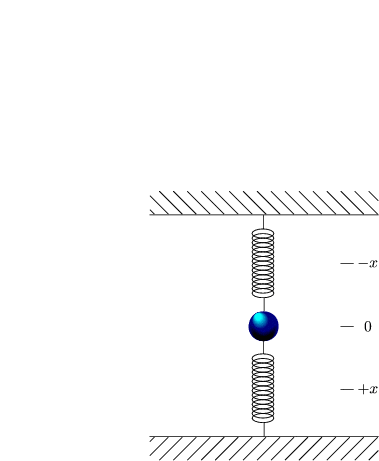
Nach dem Hookeschen Gesetz gilt F = -kx(t), wobei k die Federkonstante ist.

Frage:

Antwort:

Dies ist eine Differentialgleichung 2.Ordnung.
Beispiele für die Lösung:
$x(t) ~ ect mit c (- C$

$x(t) ~ sin(ct)$

$x(t) ~ cos(ct)$
Aus Erfahrung weiß man, daß der Bewegungsvorgang eine Schwingung mit konstanter Frequenz (periodisch) ist, solange er keine Dämpfung erfährt. Die Frequenz ergibt sich aus:
$n = 1-= -w- T 2p$
Die Lösungsfunktion ergibt sich durch Superposition der zuvor aufgezählten Lösungen:
$|----------------------| |x(t) = Asinwt+ B coswt | -----------------------$
Wir setzen diesen Ansatz in die Bewegungsgleichung F = m(t) = -kx(t) ein:
$F = mw2 (-A sin wt- B coswt) = k(- Asinwt- B coswt)$
Für alle t muß gelten:
$V~ -k-[1 ] mw2 = k ==> w = -- - m s$
hängt somit nur von k und m ab, jedoch nicht von der Amplitude. Wir setzen die Lösung in die Differentialgleichung ein und erhalten:
$|---------------------------------| | (V ~ --) (V ~ --) | |x(t) = A sin k-t + B cos k-t | ---------------m--------------m----$
- 1.Randbedingung:
  Die Auslenkung für t = 0 muß gleich 0 sein: x(t = 0) = x₀ = B.
- 2.Randbedingung:
  An den Extrema muß die kinetische Energie verschwinden: p(0) = m(0) = 0.
Die zweite Bedingung ist nur erfüllt, wenn A = 0. Damit ist x(t) = x₀ cost ist die klassische Lösung für den Hookeschen Oszillator.

1.1.1 Energie des Systems (aus Energieerhaltung)

Allgemein setzt sich diese aus kinetischer und potentieller Energie zusammen:
$2 E(t) = p--+ V (x) 2m$
Mit der potentiellen Energie
$integral x integral x k V(x) = -F (x')dx'= - (-kx') dx'= -x2 0 0 2$
ergibt sich dann durch Einsetzen:
$|----------------| |E(t) =-p2 + kx2 | -------2m----2---|$
Des weiteren folgt mit p = mx und x = x₀ cost:
$( ) -1- md-(x0coswt) 2 1 2 2 w2- 2 2 2 1 2 2 E(t) = 2m dt + 2kx0cos (wt) = 2 m x0(- sinwt) + 2kx0cos wt$
Aus ² = ergibt sich schlußendlich:
$( ) E(t) = 1kx20 cos2wt+ sin2wt = 1kx20 = const. 2 2$
Die Energie ist zu allen Zeitpunkten der Bewegung konstant.