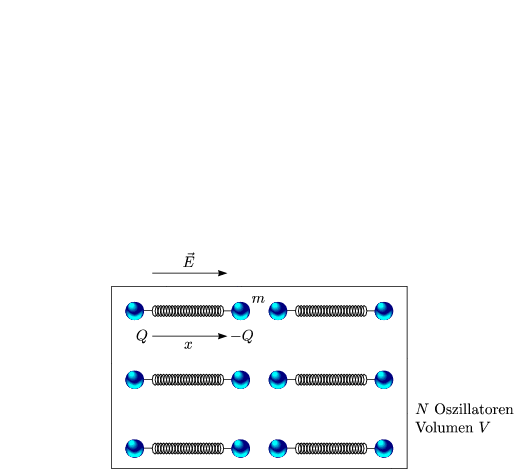

Wir hatten die Newtonschen Bewegungsgleichungen eingesetzt:
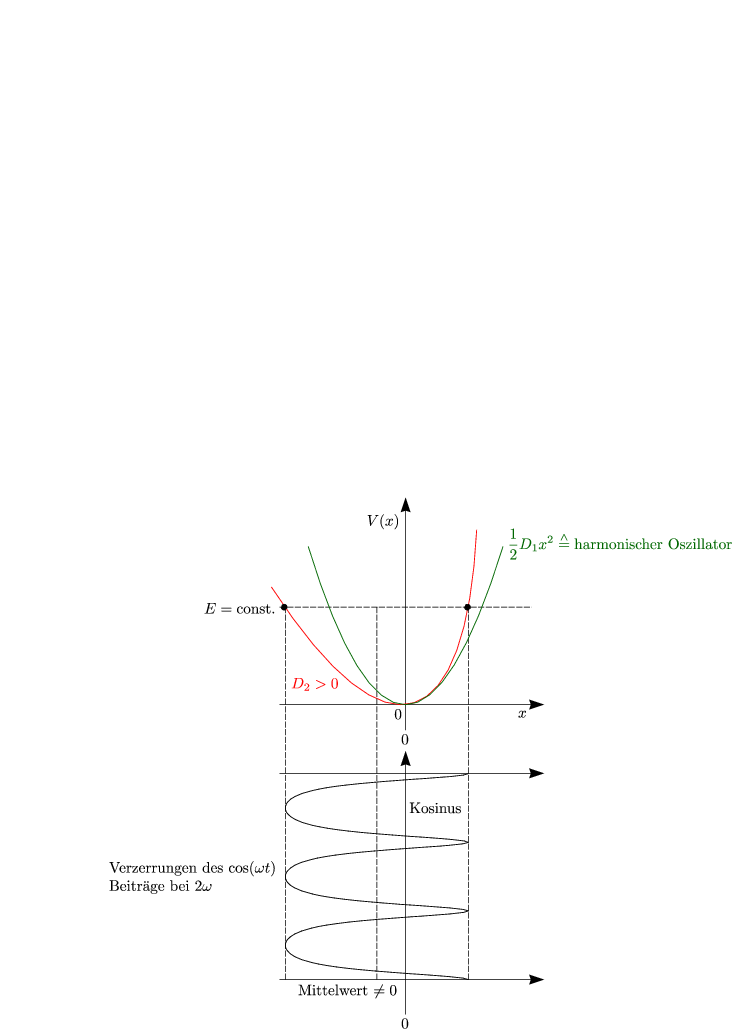
Im Gegensatz zu Kapitel 2.2 lassen wir jetzt die höheren Terme nicht weg. Bei
großen Feldstärken E (meist nur durch LASER erreichbar) wird auch die
Auslenkung x groß und |D2x2|/«|D1x|. Wir können wir diese nichtlinearen
Differentialgleichungen lösen? Die generelle Idee ist nun folgende. Wir führen eine
Störungsrechnung mit einem sogenannte Kleinheitsparameter ![]() « 1 ein. Wir ersetzen
somit E durch
« 1 ein. Wir ersetzen
somit E durch ![]() . E und machen folgenden Ansatz:
. E und machen folgenden Ansatz:
Wir setzen den Ansatz ein und sortieren nach Potenzen von ![]() . Dazu betrachten wir
die verschiedenen Ordnungen:
. Dazu betrachten wir
die verschiedenen Ordnungen:
Die Ordnung ![]() ' hatten wir in Kapitel 2.2 bereits diskutiert:
' hatten wir in Kapitel 2.2 bereits diskutiert:
Dann folgt für die lineare optische Suszeptibilität:
Für die Ordnung ![]() 2 gilt:
2 gilt:
Aus Kapitel 2.2 folgt:
Mit E(t) = E0 cos(![]() t) und mit cos2(
t) und mit cos2(![]() t) =
t) = ![]()
![]() ergibt sich folgende
Bewegungsgleichung:
ergibt sich folgende
Bewegungsgleichung:
Es gibt somit einen Term, der mit der Frequenz 2![]() oszilliert und einen, der
überhaupt nicht oszilliert. Für die Lösung folgt:
oszilliert und einen, der
überhaupt nicht oszilliert. Für die Lösung folgt:
![|-----------------------------------------------------------------------|
| (2) D2 (V e0)2 ( (1) )2 E20 [ 2 1 ] |
x (t) = - m- NQ-- x (w) -4-. _O_2---(2w)2 cos(2wt)+ _O_2- |
| ------- ------- |
| os2z- tilleie Hratrm moitni2wsch /\ =e ZeVitelirschchikoebnusntagn /\ =te |
| GleOicphtviserchteeilung |
------------------------------------------------------------------------](ex726x.gif)