4.1 Evaneszente Wellen

4.1 Evaneszente Wellen

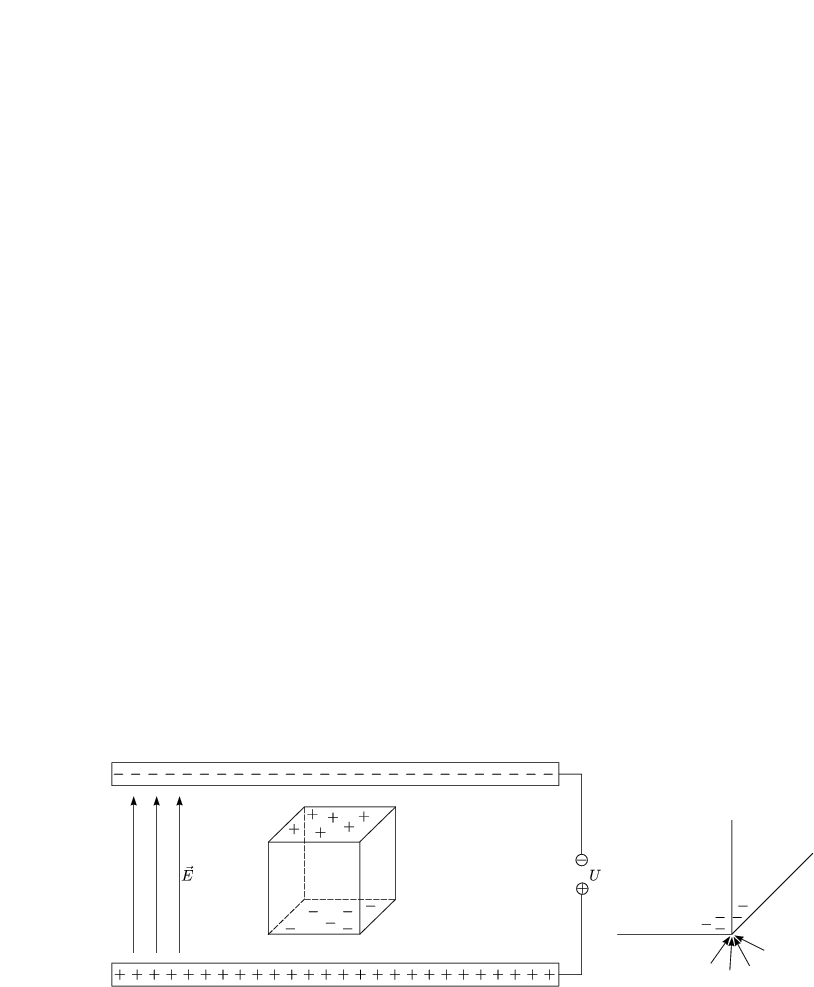
Was passiert, wenn wir den Spalt in Kapitel 3.4.2 immer kleiner machen, d.h. b < oder sogar b « ?

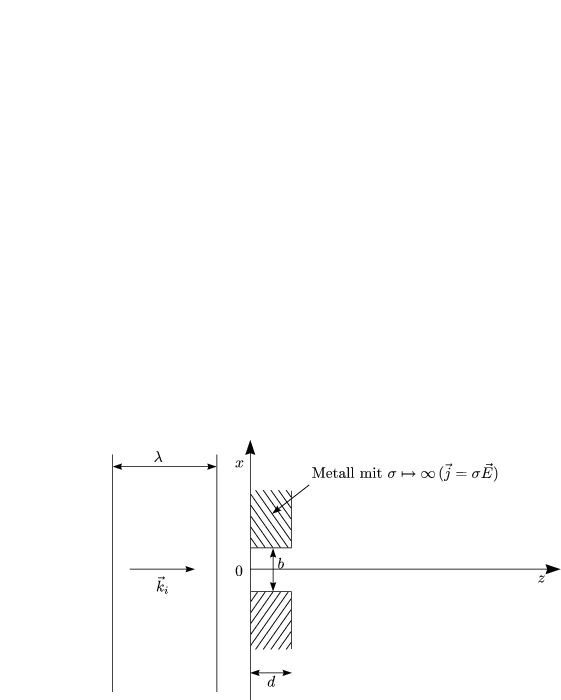
Wir nehmen jetzt also an, daß b « d (oder formal d).

Randbedingungen:

( ) ( ) b b E x = - 2 = E x = 2 = 0

Wir verwenden folgenden Ansatz (im Spalt):

( ) ( ) E = E0ei(kyy+kzz-wt)cos x.p = E0ei(+kzz-wt)cos x-.p ebene-Welle,k=0- --- b--- b y steWheelndlee

Wir setzen diesen Ansatz in die Wellengleichung ein:

1-@2- /_\ E - c20 @t2 E = 0

2 (p-)2 w2- kz + b = c20

Wir berechnen die Phasengeschwindigkeit v_ph:

vph = w-= V~ ---w----- kz w22- (p)2 c0 b

Wir dividieren durch , wobei wir erhalten:

-----c0----- vph = V~ ---c20(p)2 1 - w2 b

Außerdem folgt mit = :

c c c vph = V~ ----0--(-)-= V~ -----02-(--)-= V~ ---0(--)- > c0 1- k-0 2 pb 2 1- (c2p0)2 pb2 1 - c2b02

c0 c0 vph '--> oo f¨ur2b = 1 <==> b = 2

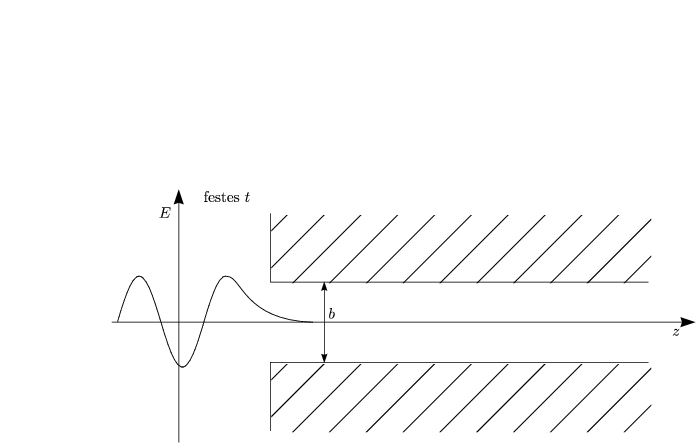
Es entstehen exponentiell gedämpfte Wellen in z-Richtung. Solche experimentell gedämpften Wellen nennt man auch evaneszente Wellen ( $/\ =$ Tunneln von Licht).

Feldverstärkung:

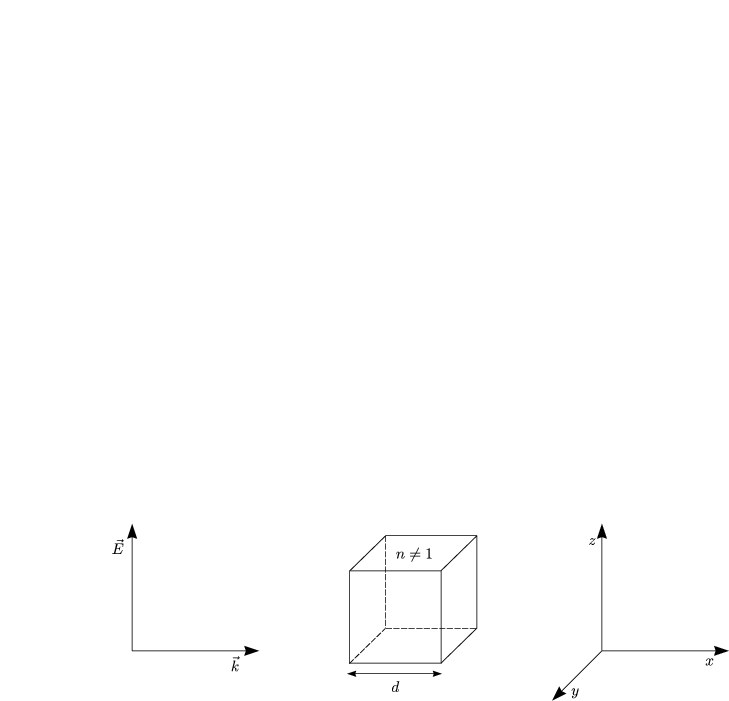
d sei die Ausdehnung eines Objekts mit d « , d.h. formal geht gegen unendlich und somit gegen 0 $/\ =$ Elektrostatik

Feldverstärkung (z.B. Blitzableiter)
Depolarisation, _Ecke ||