Hierbei verschwindet der Widerstand „sprunghaft“ bei Tc. Im folgenden wird Tc für verschiedene Element und Verbindungen aufgelistet:
| Elemente | Tc [K] | Verbindungen | Tc [K] |
| Al | 1,19 | NbSn2 | 2,6 |
| Sn | 3,72 | Nb3Sn | 18,0 |
| Hg | 4,15 | Nb3Ge | 23,2 |
| Pb | 7,2 | La1,8Sr0,8CnO4 | 36,2 |
| Nb | 9,2 | YBa2Cu3O7 | 92 |
| HgBa2Ca2Cu3O8+x | 133 | ||
Supraleitung tritt aufgrund der starken B-Felder nicht in Ferromagneten auf. Auch ist sie in „guten“ Metallen (Au, Ag, Cu, Pt) nicht möglich, da hier die Streuung am Gitter (Elektron-Phonon-Wechselwirkung) wichtig ist.
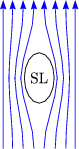
Supraleiter sind absolute Diamagnete und ideale Leiter. Aus ![]() = -1 folgt nämlich
= -1 folgt nämlich
![]() = -
= -![]() und damit B =
und damit B = ![]() 0(H + M) = 0. Legt man bei T < Tc ein äußeres Feld an,
so wird das äußere Feld verdrängt. Dies würde jedoch auch bei einem idealen Leiter
auftreten. Beim Meißner-Ochsenfeld-Effekt haben wir jedoch ein Verhalten wie
folgt:
0(H + M) = 0. Legt man bei T < Tc ein äußeres Feld an,
so wird das äußere Feld verdrängt. Dies würde jedoch auch bei einem idealen Leiter
auftreten. Beim Meißner-Ochsenfeld-Effekt haben wir jedoch ein Verhalten wie
folgt:
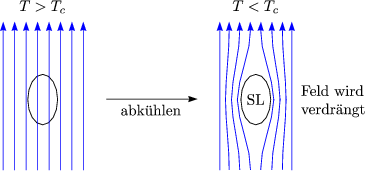
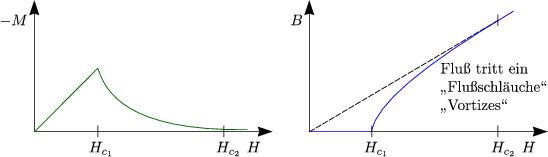
Als Beispiel einer Realisierung betrachten wir das Vortex-Wirbelgitter:
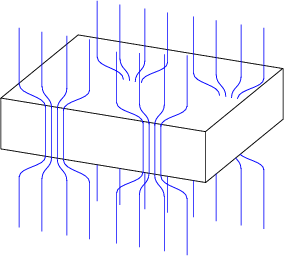
Es besteht ein quantisierter Fluß ![]() 0 =
0 = ![]() und damit entstehen
Supraströme.
und damit entstehen
Supraströme.
Die erste phänomenologische Theorie der Supraleitung stellte F.U.H LONDON im Jahre 1935 auf:
Wegen ![]() =
= ![]() ist E = 0 und damit gilt j = const. Aus der
MAXWELL-Gleichung rot
ist E = 0 und damit gilt j = const. Aus der
MAXWELL-Gleichung rot![]() = -
= -![]() folgt:
folgt:
Dies entspricht einem idealen Leiter.
Dies führt zu einer endlichen Eindringtiefe des B-Feldes.
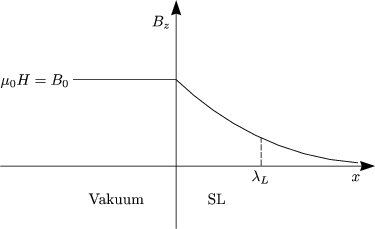
![]() L nennt man LONDONsche Eindringtiefe und ns bezeichnet die Dichte
der supraleitenden Ladungsträger. Es gilt ns
L nennt man LONDONsche Eindringtiefe und ns bezeichnet die Dichte
der supraleitenden Ladungsträger. Es gilt ns![]() 0 für T
0 für T![]() Tc und damit
Tc und damit
![]() L
L![]()
![]() .
.
Mit konstantem Druck und ![]() = -1 ergibt sich des weiteren:
= -1 ergibt sich des weiteren:
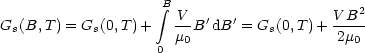
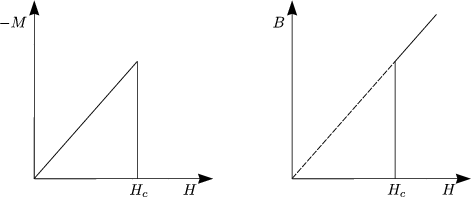
Die Feldverdrängung erhöht Gs. Der Übergang zum Normalleiter findet statt bei
Bc = ![]() 0Hc.
0Hc.
PAULI-Para- und LANDAU-Dia-Magnetismus seien vernachlässigt.
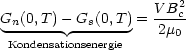
Tc und Bc sind gekoppelt.
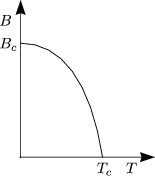
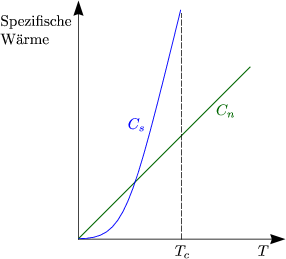
Berechnen wir weiterhin die spezifische Wärme; mit S = -![]() und C = T
und C = T![]() folgt:
folgt:
Für T![]() Tc folgt Bc
Tc folgt Bc![]() 0:
0:
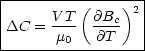
Hierbei handelt es sich um einen endlichen Sprung.