
Die Idealisierung ist, daß wir einen idealen Leiter als Begrenzung haben.

Der Aufbau der Oberflächenladung sei „instantan“.
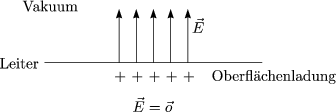
Die Oberflächenladung kompensiert das elektrische Feld im Innern des Leiters.
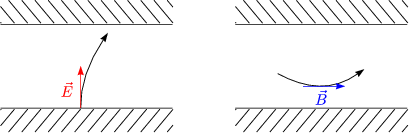
Wir betrachten ein zeitlich schnell veränderliches Magnetfeld. Dieses wird durch Induktionsströme abgeschirmt (keine Dämpfung).

Außerhalb, aber nahe an einem idealen Leiter, gilt:
![]() steht also senkrecht zu Oberfläche, während
steht also senkrecht zu Oberfläche, während ![]() parallel zu dieser
steht.
parallel zu dieser
steht.
Wir betrachten die Wellenausbreitung in einem Hohlleiter, dessen Querschnitt beliebig aber konstant sein soll. Der Symmetrieachse durch den Hohlleiter liege dabei in z-Richtung. Der zu verwendende Ansatz lautet:
Leiten wir diese beiden Gleichungen nach t ab, so ergibt sich ein Faktor -i![]() .
Die Maxwellgleichungen in Vakuum (
.
Die Maxwellgleichungen in Vakuum (![]() = j = 0) lauten:
= j = 0) lauten:
Damit gilt:

Analog gilt:
Vor einigen Wochen hatten wir:
k ist zunächst unbekannt (eventuell komplex). Wir definieren nun einen transversalen Laplace-Operator:
Die Wellengleichung geht wegen der speziellen z-Abhängigkeit über in:

Wir haben somit sechs Gleichungen für die Komponenten von ![]() und
und ![]() .
Unser Ziel ist es, eine Gleichung für Ez (oder Bz) zu erhalten und die
restlichen fünf Komponenten durch Differentiation aus Ez (oder Bz) zu
bekommen. Dazu zerlegen wir
.
Unser Ziel ist es, eine Gleichung für Ez (oder Bz) zu erhalten und die
restlichen fünf Komponenten durch Differentiation aus Ez (oder Bz) zu
bekommen. Dazu zerlegen wir ![]() und
und ![]() in Anteile senkrecht und parallel zu
in Anteile senkrecht und parallel zu
![]() z.
z.
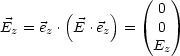
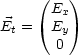
Nach Umrechnung der Maxwell-Gleichungen (Jackson, Greiner (Seiten 374/375, 2 Seiten)) folgt:
Vorsicht ist geboten, denn aufgrund der Randbedingungen gilt:
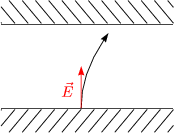
![]() ist parallel zur Leiteroberfläche.
ist parallel zur Leiteroberfläche.
Aus ![]() O = 0 und (**) folgt:
O = 0 und (**) folgt:
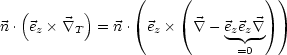
![]() O enthält nur die Ableitung in Richtung der Oberfläche:
O enthält nur die Ableitung in Richtung der Oberfläche:
Damit folgt:
Und somit gilt:
Das Ziel ist nun, die Abhängigkeit von Ez und Bz aus den zweidimensionalen
partiellen Differentialgleichungen (*) und den Randbedingungen B![]() und E
und E![]() aus (**) und (* * *) zu bestimmen.
aus (**) und (* * *) zu bestimmen.
Das ändert nichts daran, daß die Randbedingungen erfüllt sein müssen:
Schaut man die obigen Gleichungen (**) und (* * *) an, so müßte man vermuten, daß alle Komponenten des elektrischen und magnetischen Feldes gleich Null sind. Dies ist aber nicht so, da nun folgendes gilt:
Die Beziehungen (**) und (* * *) gelten somit nicht mehr. Die Ausbreitung findet mit Lichtgeschwindigkeit statt, als ob keine Randbedingungen bestehen würden. Damit werden wir uns später genauer auseinandersetzen.
Es gilt nun:
Aus der zweiten Gleichung folgt dann:
Somit lösen wir nach ![]() T und
T und ![]() T auf und erhalten:
T auf und erhalten:
Für Ez gilt die zweidimensionale Differentialgleichung.
Die Randbedingung lautet:
Alle Felder ergeben sich aus einer Funktion Ez(x,y). Analog gilt für die transversal elektrischen Lösungen:
Entscheidend ist nun folgende Wellengleichung:
Es handelt sich dabei um eine partielle Differentialgleichung 2.Ordnung für den transversal elektrischen und den transversal magnetischen Fall. Wir setzen nun folgendes fest:

Wir untersuchen nun den transversal elektrischen Fall:
Wir nehmen folgenden Ansatz zur Lösung der Differentialgleichung:
Dieser Ansatz erfüllt die Randbedingungen. Wir setzen den Ansatz in die Differentialgleichung ein, womit sich dann ergibt:
Wir lösen nach k auf:

Für ![]() <
< ![]() min wird k imaginär.
min wird k imaginär.
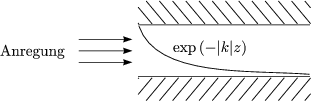
Bz fällt infolgedessen exponentiell ab. Der Zusammenhang zwischen dem
Wellenvektor k und ![]() definiert hierbei die Phasengeschwindigkeit:
definiert hierbei die Phasengeschwindigkeit:
![|--------------------------|
w- |-----------w----------- |
k = vph =| V~ 2 2 2[(m)2 (n )2].c |
| w - p c a- + -b |
---------------------------](th1591x.gif)
Der Nenner ist größer als 1. Die Phasengeschwindigkeit ist somit größer als die Lichtgeschwindigkeit. Von Bedeutung ist aber die Gruppengeschwindigkeit:
![| V~ --------[(--)---(-)-]---|
| w2- p2c2 ma- 2 + nb 2 |
dw-= d1k-= |-----------------------.c |
dk dw ------------w--------------|](th1592x.gif)
Der Ausdruck geht gegen Null für ![]()
![]()
![]() min.
min.

Diese Gleichungen erinnern dan die Ausbreitung im Vakuum ohne Hohlleiter. Mit den Maxwellgleichungen gilt:
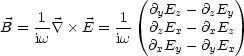
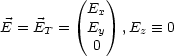
Also gilt damit:
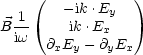
Mit Bz = 0 folgt:
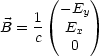
Wegen Bz = 0 muß gelten:
Dabei handelt es sich um die Integrabilitätsbedingung in zwei Dimensionen. ![]() T läßt
sich als Quadrat eines Potential darstellen.
T läßt
sich als Quadrat eines Potential darstellen.
Dies ist also die Lösung eines zweidimensionalen Potential-Problems:

Dies ist der Fall, wenn das Gebiet einfach zusammenhängend ist.

Es handelt sich um ein Koaxialkabel. Da wir eine lineare Dispersionsrelation haben, breitet sich jeder Puls mit gleicher Geschwindigkeit aus.
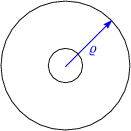
Eine mögliche Lösung des Problems ist:
Die Konstanten A und ![]() 0 werden an die Randbedingungen
0 werden an die Randbedingungen ![]() (
(![]() 1) und
1) und ![]() (
(![]() 2)
angepaßt:
2)
angepaßt: