3.2 Freie Energie F = F(V,T) und freie Enthalpie G = G(p,T) (Gibbs-Energie)

Wir betrachten einen Wärmeaustausch bei V = const. und gehen aus von dS - > 0 und dem 1.Hautpsatz dU = dq - pdV dq, wobei pdV 0 gilt.

Wir multiplizieren auf beiden Seiten mit -T und erhalten:

Wir fassen den Term auf der linken Seite als Differential zusammen:

Zusammenfassung zu F = F(V,T):

1. F U - TS d.h. dF dU - TdS bei T,V = const.
2. F ist Zustandsfunktion!
3. ₁²dF = F₂ - F₁ < 0 Minimum im Gleichgewicht

Die freie Enthalpie G = G(p,T):

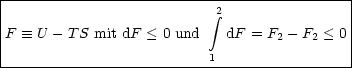
Wir betrachten einen Wärmeaustausch bei p = const.:

Auch hier multiplizieren wir mit -T, womit sich dH - TdS < 0 ergibt. Wenn T = const. gilt, folgt daraus d(H - TS) < 0. Wir erhalten damit

G = G(p,T) = H_TS als Zustandsfunktion mit dG < 0.

3.2.1 Interpretation von F(V,T) bzw. G(p,T)

Freie Energie F:

• Isotherme reversible Zustandsänderung
• dF = dU - TdS = dq_rev + dw_mech - TdS = dw_mech (maximale) mechanische Nutzarbeit (nach 1.Hauptsatz)

Freie Enthalpie G:

• Für Reaktionen bei p,T =const. gibt G die maximal freiwerdende Energie (über die pV -Arbeit hinaus) an.

3.2.2 Mastergleichung für die innere Energie

Da U eine Zustandsfunktion ist, kann man sie als totales Differential schreiben:

Daraus folgt nun durch Vergleichen:

Da U eine Zustandsfunktion ist, läßt sich außerdem der Schwarz’sche Satz anwenden:

Wir haben hier eine der sogenannten MAXWELL-Relationen hergeleitet. Zu U(V,T) thermodynamische Zustandsgleichung:

3.2.3 Mastergleichung für F = F(V,T)

Betrachten wir die Mastergleichung für F:

Das totale Differential von F lautet:

Wir führen einen Koeffizientenvergleich mit der Mastergleichung durch:

Wir erhalten somit wieder eine der MAXWELLschen Relationen:

3.2.4 Mastergleichung für G = G(p,T)

Betrachten wir G H - TS.

(3.2)

Der Koeffizientenvergleich ergibt:

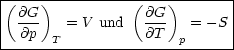
Daraus erhalten wir erneut:

Aus dG < 0 folgt G₂ - G₁ < 0. Im Gleichgewicht gilt dG = 0.

3.2.5 Temperaturabhängigkeit von G(T,p) bei p=const.

• Qualitativ:

  Wir veranschaulichen dies graphisch folgendermaßen:

  

• Quantitativ:

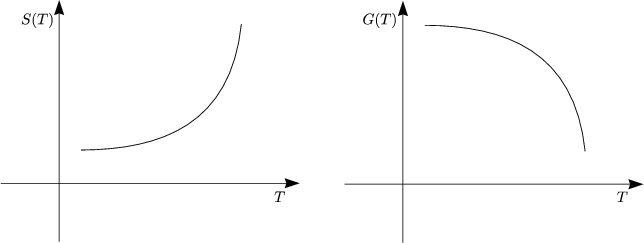
  Aus G = H - TS folgt:

  

  Wir betrachten:

  

  Es gilt hier also folgender Zusammenhang:

  

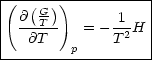
  Beispielsweise gilt für chemische Reaktionen G = G₂ - G₁:

  

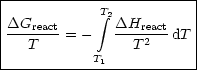
  Diesen Ausdruck nennt man Gibbs-Helmholtz-Beziehung.

3.2.6 Druckabhängigkeit von G(T,p) bei T=const.

Hier gilt:

• Qualitativ:

  

• Quantitativ:

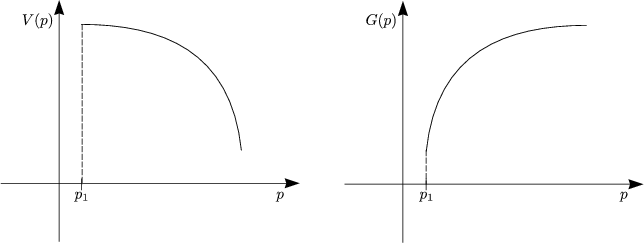
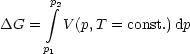
  Wir setzen die Kenntnis der Zustandsgleichung unseres Systems p = p(V,T) bzw. V = V (p,T) voraus. Beispielsweise ist für Festkörper oder Flüssigkeiten V schwach p-abhängig:

  

  Andererseits gilt für ein ideales Gas die Gasgleichung pV = nRT, woraus folgt:

  

  Als Standardzustand wird der Zustand bei p = 1atm bezeichnet: