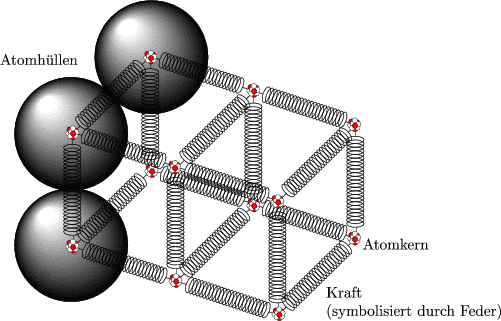
Form von Materie, in der interatomare Kräfte zur dreidimensionalen stabilen Anordnung von Atomen führen.
| Kristalle | Regelmäßige Anordnung |
| Amorphe Festkörper | unregelmäßige Anordnung |


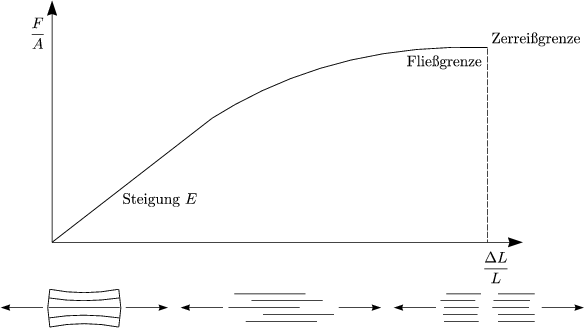
E bezeichnet man als Elastizitätsmodul (englisch: YOUNG’s-Modulus).
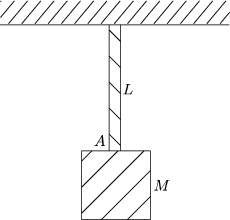
Mit L = 2m, ![]() = 2cm, E = 2,5 . 1011
= 2cm, E = 2,5 . 1011![]() und M = 9,5t berechnen
wir:
und M = 9,5t berechnen
wir:
Speziell für Gummi gilt:
Gummi zerreißt allerdings vorher.
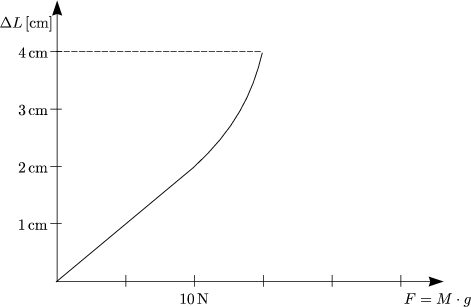
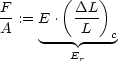
![]() L ist die Verlängerung vor dem Zerreißen.
L ist die Verlängerung vor dem Zerreißen.
![|------------|--[--]---|--[--]----|
|------------|E--Nm2----|Er-mN2-----|
|Stahl |2,5.1011 |4- 30.108 |
|Glas |7.1010 |3- 20.107 |
|Spinnenseide | |2,4 .108 |
|Sehne | |108 |
-Gummi------------------107--------](ex1125x.gif)
Für Gummi gilt Mmax = 320kg.

Es gilt mit der sogenannten POISSONzahl ![]()
![]() 0,3:
0,3:
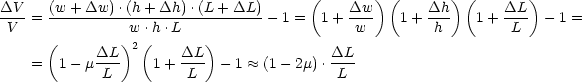 | (5.1) |
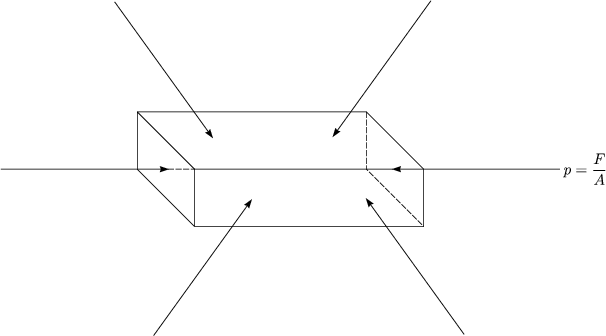
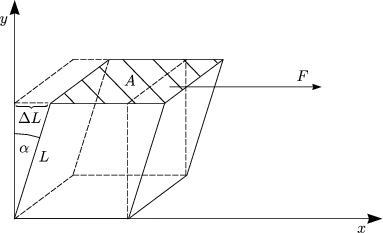
Es gibt dabei folgende Zusammenhänge:
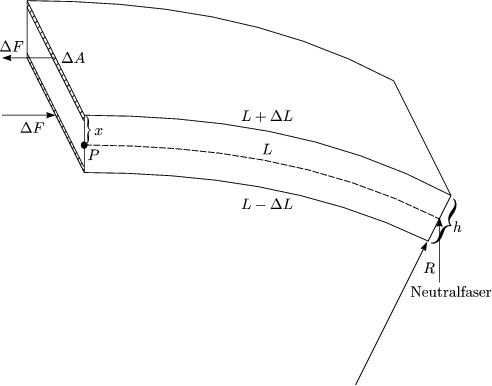
Wir errechnen das Drehmoment um P:
Mit ![]() = E .
= E .![]() und
und ![]() =
= ![]() , wobei R der Krümmungsradius ist, erhalten
wir:
, wobei R der Krümmungsradius ist, erhalten
wir:
Durch Integration folgt dann schließlich:
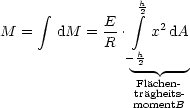
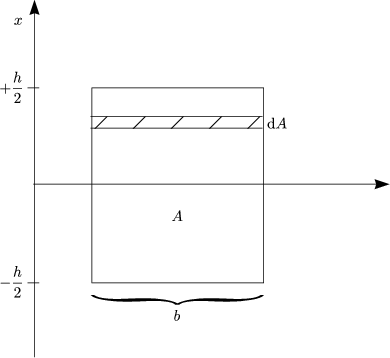
Die allgemeine Formel zur Berechnung des Flächenträgheitsmomentes lautet:
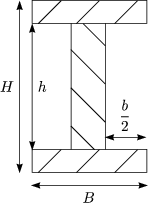
Als Beispiel betrachten wir uns:
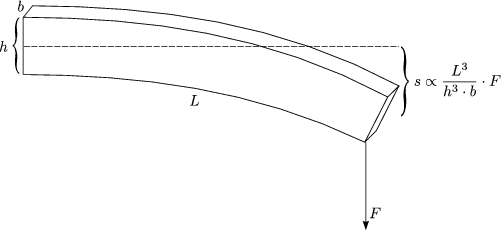
Allgemein gilt:
Damit erhalten wir für diesen Fall:
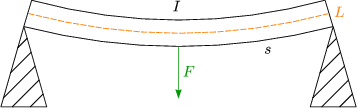
Hier gilt:
Wir beschäftigen uns mit folgenden Beispielen:
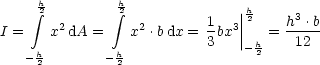
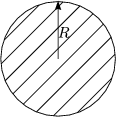
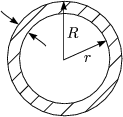
Vergleichen wir die Biegung eines Zylinders bzw. Rohres gleicher Fläche mit R - r = 0,2R, welche an einer Seite eingespannt sind:
Eine Verdrehung entspricht einer Scherung der einzelnen Elemente.
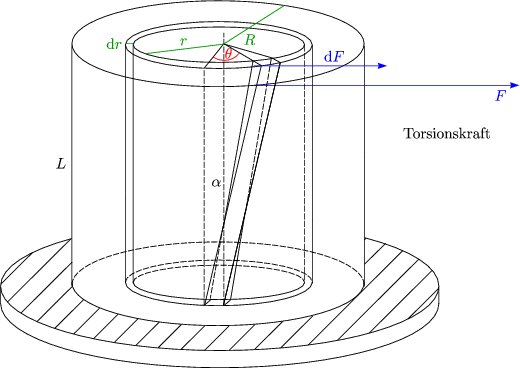
Des weiteren gilt:
Für die Zylinderhülse erhalten wir nun:
Für das Drehmoment des gesamten Zylinders gilt:
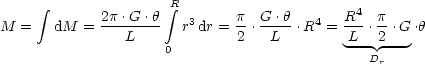
Allgemein gilt:
Dr nennt man entweder Richtmoment oder auch Torsionsmodul.
Um bestimmten Winkel ![]() zu erhalten!
zu erhalten!
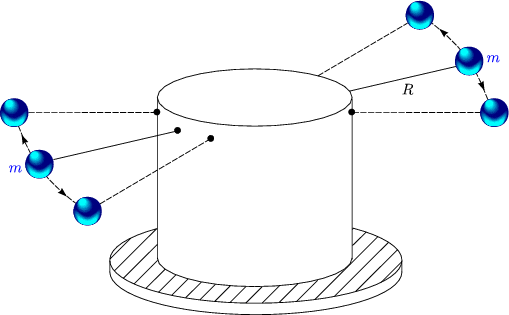
Auch hier berechnen wir das Drehmoment:
J ist das Massenträgheitsmoment, welches wir schon kennen. Es gilt beispielsweise JHantel = 2mR2. Die Lösung der obigen Differentialgleichung finden wir mit dem Ansatz:
| Eichsubstanz | Mokshärte |
| Talk | 1 |
| Gips | 2 |
| Kalkspat | 3 |
| Flußspalt | 4 |
| Apatit | 5 |
| Feldspat | 6 |
| Quarz | 7 |
| Topas | 8 |
| Korund | 9 |
| Diamant | 10 |
Weitere Beispiele sind:
| Eichsubstanz | Mokshärte |
| Aluminium | 2,3 - 2,9 |
| Eisen | 3,5 - 4,5 |
| Stahl | 7 |
| Graphit | 1 - 2 |
| Glas | 6 - 6,5 |
| Rubin, Smaragd, Saphir | 9 |
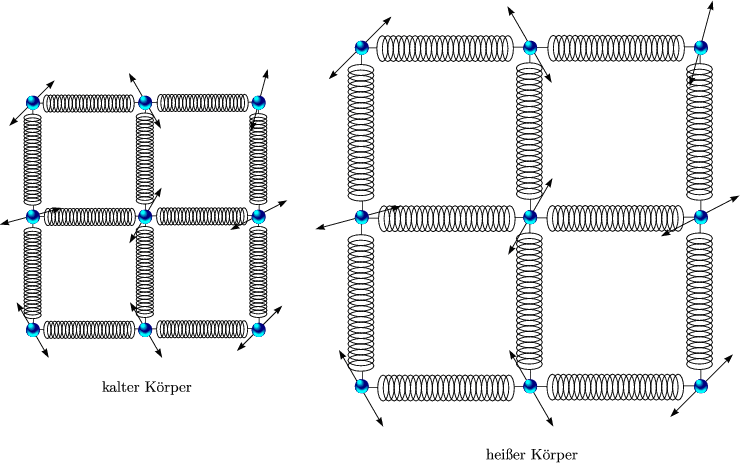
Es ergibt sich folgende Längenänderung:
![----------------------------------[-]--
-Material----Ausdehnungskoeffizient a-1K---
-Aluminium--24-.10--6-------------------
Stahl 10 .10- 6
Quarz 0,4.10-6
Glas 9 .10- 6
---------------------------------------](ex1179x.gif)
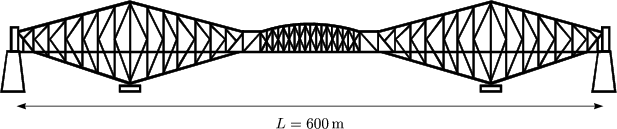
Die Brücke wird auf beiden Seiten um 24 cm länger.


Der Bimetallstreifen wird unter anderem verwendet für:

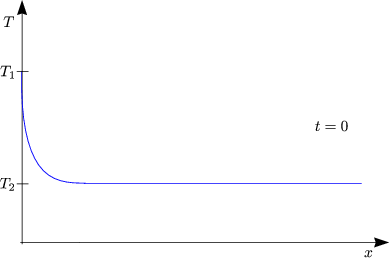
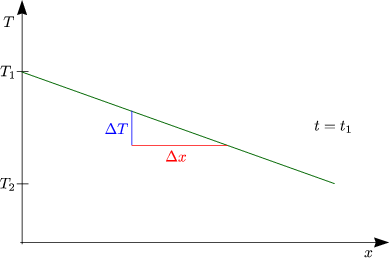
Material homogen, keine seitlichen Wärmeverluste
![-----------------------------------[W--]-
-Material----Thermische Leitf¨ahigkeit c-mK--
Silber 420
Aluminium 220
Gestein 2,5
Wasser 0,6
-Luft-------0,026------------------------](ex1196x.gif)
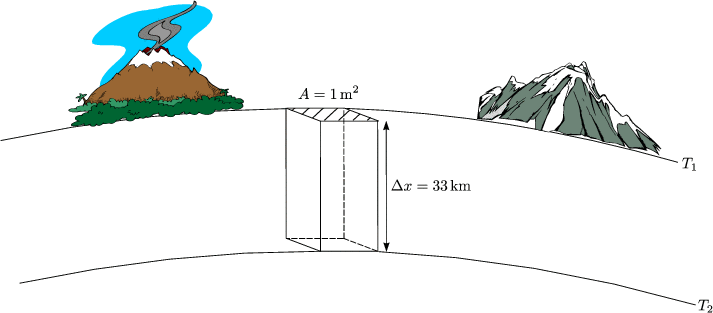
Für T1 = 10oC wollen wir T2 berechnen: