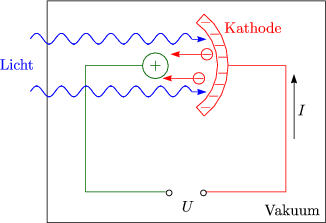
Licht besteht aus einzelnen Korpuskeln ( Photonen).
h nennt man das PLANCKsche Wirkungsquantum. Dessen Wert beträgt 6,626 . 10-34 Js. Eine interessante Konsequenz hieraus ist:
Damit erhält man die kinetische Masse eines Photons:
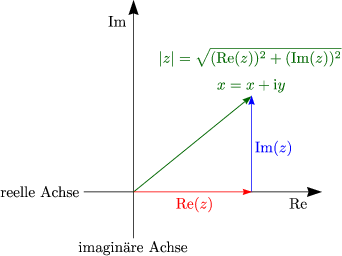
Eulersche Darstellung und Polarkoordinaten-Darstellung einer komplexen Zahl z = x + iy sind äquivalent:
Der Beweis erfolgt mit den TAYLORentwicklungen der Funktionen ex, sin(x) und cos(x).
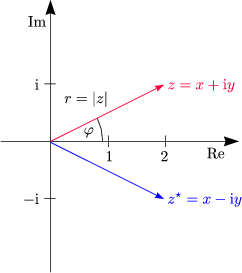
Der Betrag folgt anschaulich mittels des Satzes von PYTHAGORAS anwendbar auf die Darstellung in der komplexen Zahlenebene:
Die Projektionen auf die jeweiligen Achsen ergeben sich durch:
Die konjugiert komplexe Zahl folgt durch Spiegelung an der reellen Achse:
| z = x + iy | z* = x - iy | |||
| z = rei | z* = re-i | |||
Des weiteren lassen sich damit Sinus und Kosinus mit komplexen Exponentialfunktionen darstellen:
Im Jahre 1923 stellte DE BROGLIE die Theorie auf, daß Materie analog zu Licht eine Wellennatur besitzt:
Hieraus ergeben sich folgende Konsequenzen:

Das Elektron formt eine stehende Welle.
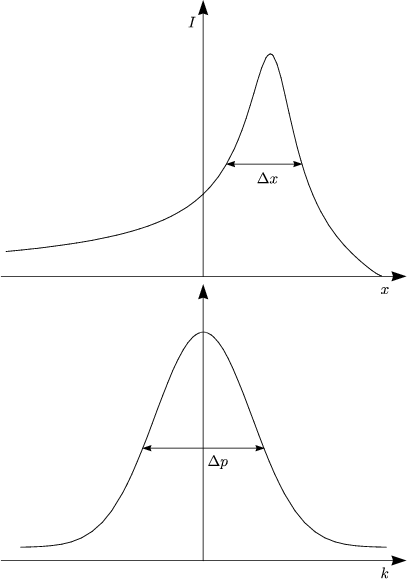
Materieteilchen treten als Wellenpakete auf.
Wir machen folgenden Ansatz:
Eingesetzt in die Differentialgleichung ergibt sich:
Hieraus folgt dann:
Hieraus folgt nun die Dispersionsrelation für freie Lichtwellen im Vakuum:
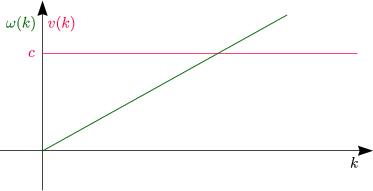
Auch gilt:
Damit gilt:
Dies entspricht der Gruppengeschwindigkeit ![]() . Somit gilt durch Integration:
. Somit gilt durch Integration:
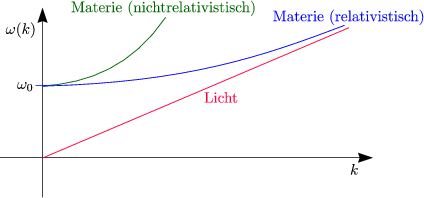
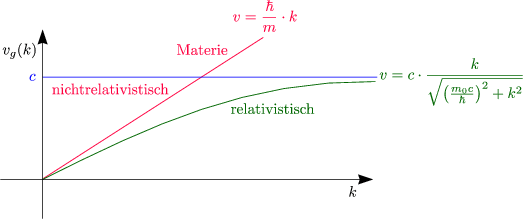
Relativistisch korrekt ist folgendes:
Damit gilt durch partielles Ableiten nach k:
Da es sich um eine partielle Differentialgleichung handelt, machen wir wieder einen Ansatz als FOURIERtransformierte:
Durch Einsetzen von ![]() (
(![]() ,t) in die SCHRÖDINGERgleichung, erhält man:
,t) in die SCHRÖDINGERgleichung, erhält man:
Man nennt diese auch KLEIN-GORDAN-Gleichung. Es wird wieder der Ansatz als FOURIERtransformierte verwendet:
Durch Einsetzen resultiert:
Für m0![]() 0 (Photonen) folgt aus der KLEIN-GORDON-Gleichung die Wellengleichung
für elektromagnetische Wellen.
0 (Photonen) folgt aus der KLEIN-GORDON-Gleichung die Wellengleichung
für elektromagnetische Wellen.
![]() ist die Auslenkung (= z).
ist die Auslenkung (= z).
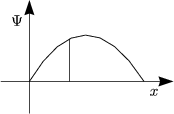
![]() ist die Feldstärke.
ist die Feldstärke.
![]() ist die Wahrscheinlichkeitsamplitude.
ist die Wahrscheinlichkeitsamplitude.
![]() (
(![]() ,t) = |
,t) = |![]() |2 =
|2 = ![]() *
*![]() wird als Aufenthaltswahrscheinlichkeit interpretiert. Es gilt
folgende sehr wichtige Normierungsrelation:
wird als Aufenthaltswahrscheinlichkeit interpretiert. Es gilt
folgende sehr wichtige Normierungsrelation:
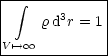
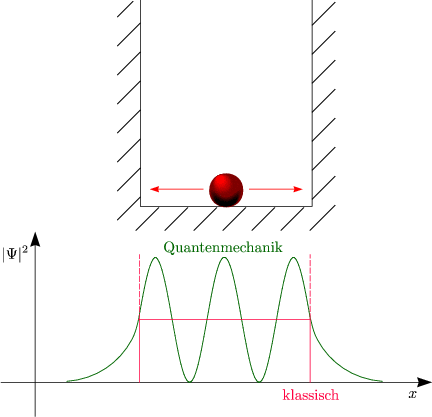
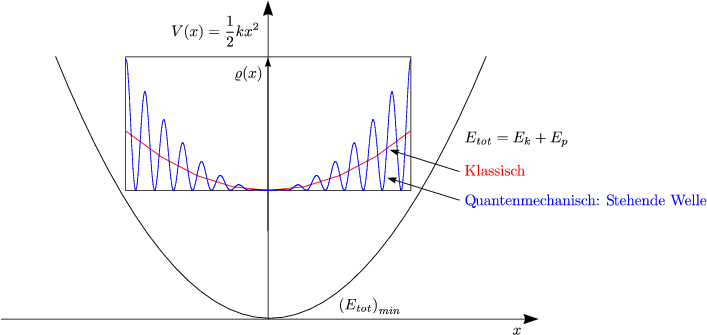
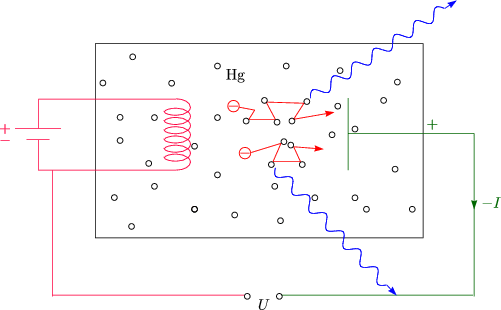
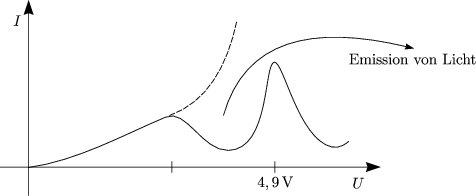
Da sich nur stehende Materiewellen im Potential befinden, sind nur diskrete Energieniveaus möglich. Dies führt also zu einer Quantelung der Energie.