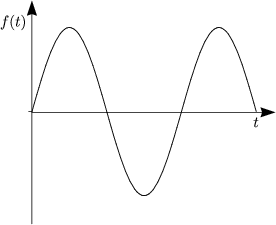
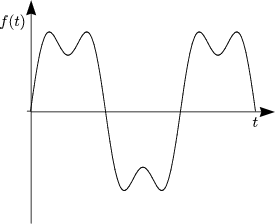
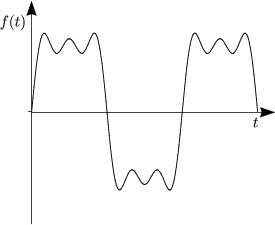
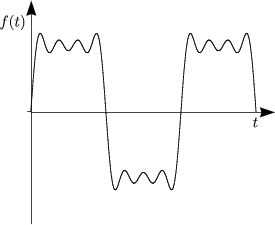
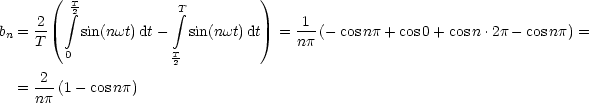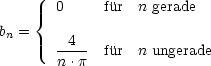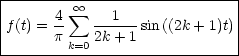- Ungedämpft
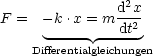
Wir verwenden folgenden Ansatz:
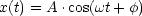
Durch Einsetzen folgt:
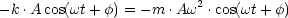
Dies gilt zu allen Zeiten t.
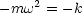
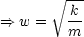
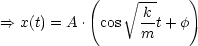
Aus der Randbedingung x(t = 0) = A folgt
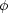 = 0.
= 0.

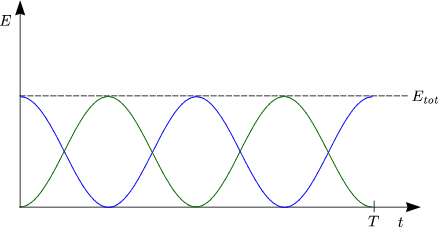
Schauen wir uns die Energiebilanz an:
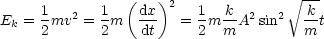
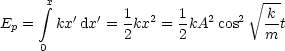
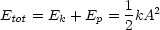
- Gedämpfte Schwingung

Wir haben folgenden Ansatz:
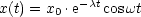
Die Phase
 wird weggelassen. Eingesetzt in Differentialgleichung ergibt:
wird weggelassen. Eingesetzt in Differentialgleichung ergibt:
Somit folgt:
(5.2) 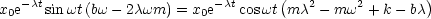
Dies gilt für alle t! Damit haben wir:
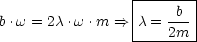
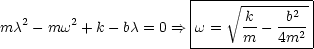
Die Lösung lautet:
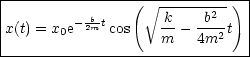
x(t) hängt stark ab von:

Diskussion:
- Keine Dämpfung: b = 0
Hierbei erhalten wir eine einfache Kosinusfunktion:
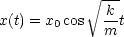
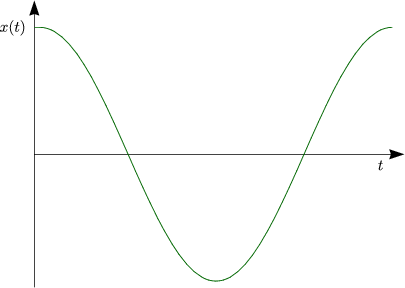
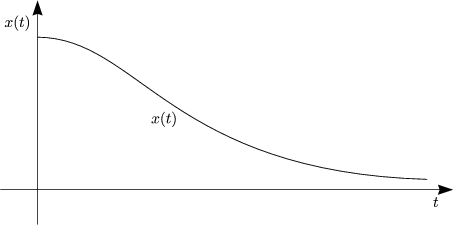
- Dämpfung schwach: b <
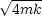
Die Schwingung wird durch eine exponentiell gedämpfte Kosinusfunktion beschrieben:

- Grenzfall: b =
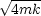
Mit
 = 0 und cos
= 0 und cos t = 1 ergibt sich eine Exponentialfunktion:
t = 1 ergibt sich eine Exponentialfunktion:
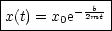
- Überdämpfung: b >
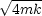
Die Kreisfrequenz
 ist imaginär! Der Kosinusansatz zur Lösung
der Differentialgleichung ist ungültig!
ist imaginär! Der Kosinusansatz zur Lösung
der Differentialgleichung ist ungültig!
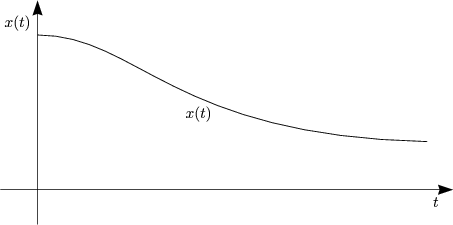
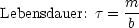
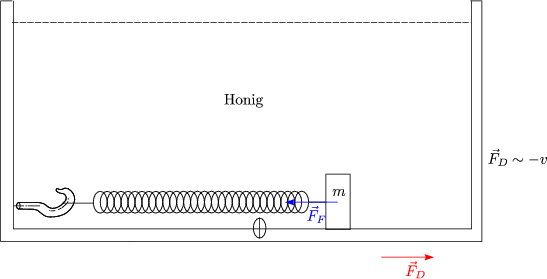
Gedämpfte Federschwingung:
Die Physik steckt in der Kraftgleichung:
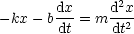
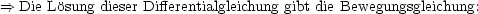
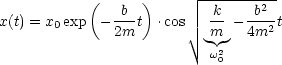
Physikalische Größen:
- Lebensdauer:

Dies entspricht der Abklingzeit, bei der die Amplitude auf
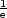 x0
abgefallen ist.
x0
abgefallen ist.
- Qualitätsfaktor:
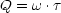
Es handelt sich um die Anzahl der Oszillationen (in rad) während der Abklingzeit.
Beispiele:
- Stimmgabel: Q
 104
104
- Federpendel: Q
 10 - 20
10 - 20
Für die gesamte Energie gilt:
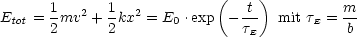
Die Energie ist somit keine Erhaltungsgröße! Sie wird umgewandelt durch Reibung in Wärme, Wirbel.
- Stimmgabel: Q
Beispiel:
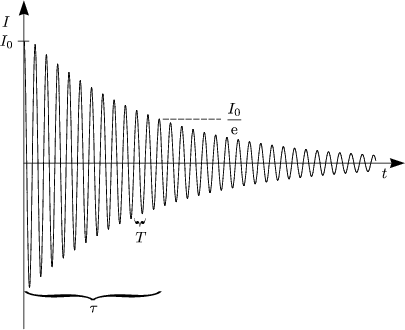
Es sei
 = 5s und T = 5ms. Damit folgt:
= 5s und T = 5ms. Damit folgt:
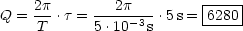
- Keine Dämpfung: b = 0
- Erzwungene Schwingungen:
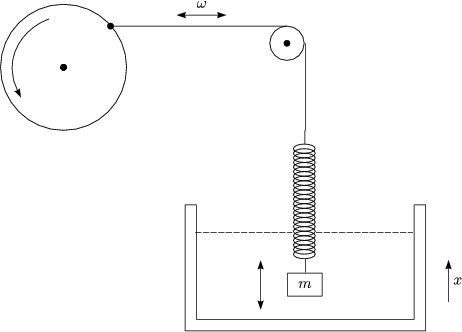
Wir betrachten ein periodisch angeregtes oszillierendes System mit Dämpfung. Die zugehörige Kraftgleichung lautet:
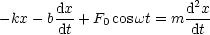
Umgeformt ergibt sich:
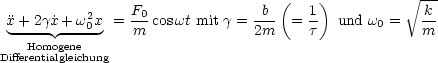
Wir verwenden folgenden Lösungsansatz:
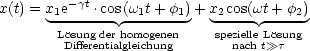
Wir beschränken uns auf eine spezielle Lösung nach t »
 . Der Ansatz
lautet:
. Der Ansatz
lautet:
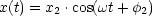
Damit folgt das Ergebnis:
- x2 =
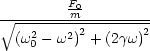
Die Amplitude ist somit frequenzabhängig! Die Herleitung findet man beispielsweise im Demtröder 11.5
- tan
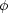 2 = -
2 = -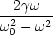
Phasenverschiebung: Schwingung der Masse hinkt der Erregerschwingung hinterher.
Diskussion: Amplitude
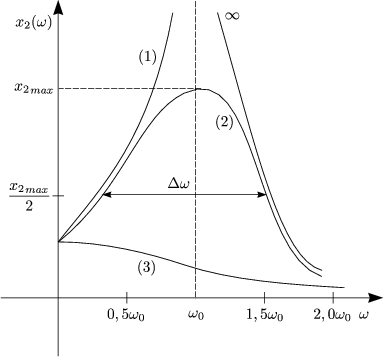
Der Wert
 der Amplitude wird theoretisch nur für
der Amplitude wird theoretisch nur für 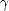 = 0 erreicht.
= 0 erreicht.
- Für
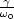 = 0 haben wir keine Dämpfung.
= 0 haben wir keine Dämpfung.
- Resonanzkurve
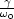 = 0,1 (schwache Dämpfung)
= 0,1 (schwache Dämpfung)
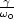 = 1 (starke Dämpfung)
= 1 (starke Dämpfung)
Die Halbwertsbreite beträgt
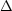

 2
2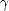 .
.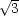 und das Full Width Half
Maximum (FWHM) beträgt
und das Full Width Half
Maximum (FWHM) beträgt 
 . Für
. Für 
 0 (d.h. b
0 (d.h. b 0) gilt x2
0) gilt x2
 ,
,

 0.
0.
- x2 =
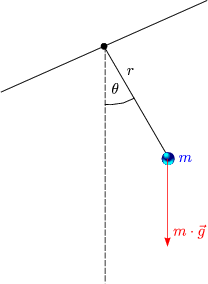
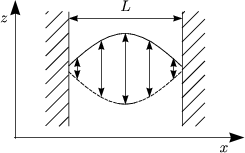
- Mathematisches Pendel
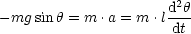
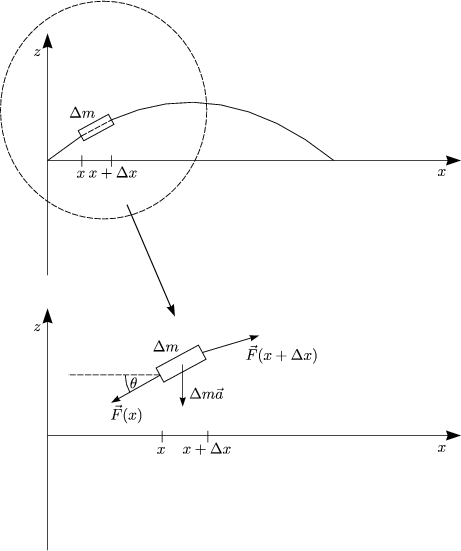
Diese Differentialgleichung ist nicht algebraisch lösbar! Wir verwenden deshalb folgende Näherung:
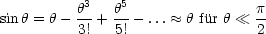
Damit erhalten wir folgende Differentialgleichung:
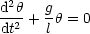
Folgender Ansatz ist sinnvoll:
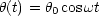
Damit erhalten wir:
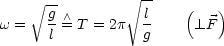
Betrachten wir außerdem folgenden Spezialfall. Für
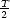 = 1s gilt:
= 1s gilt:
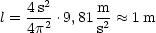
Dies ist das sogenannte Sekundenpendel.
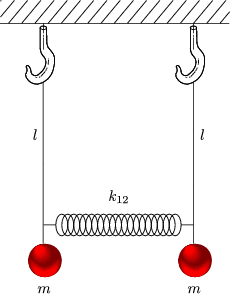
5.3.2 Vergleich zwischen Pendel- und Federschwingung
Behauptung:
Pendel, dessen Länge gleich Ausdehnung einer Feder durch ein Gewicht ist, hat die gleiche Frequenz wie die Feder.

Beweis:
Die Federdehnung ist gegeben durch:
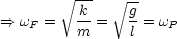
- Physikalisches Pendel
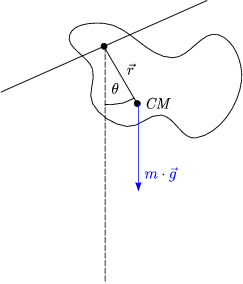
Es ergibt sich folgendes Drehmoment:
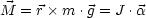
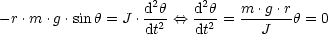
Auch hier benutzen wir die Näherung sin


 . Somit gilt für die
Lösung:
. Somit gilt für die
Lösung:
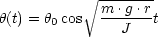
Beispiele:
- Masse konzentriert im Massenmittelpunkt:
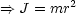
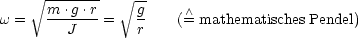
- Pendel ist dünner Stab
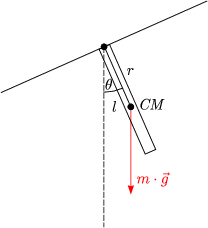
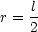
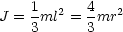
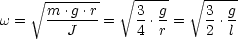
- Masse konzentriert im Massenmittelpunkt:
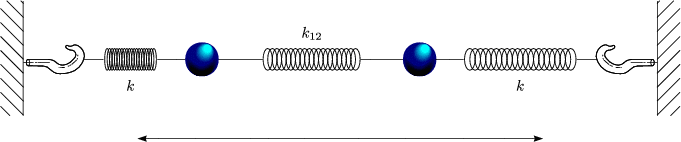
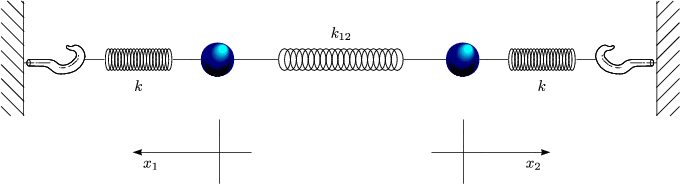
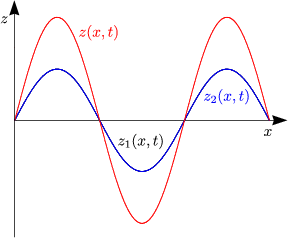
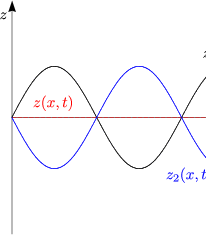
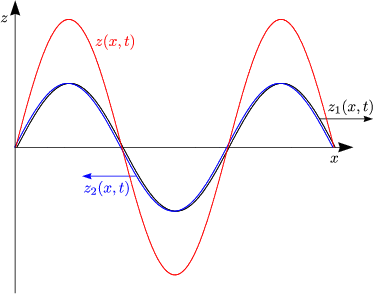
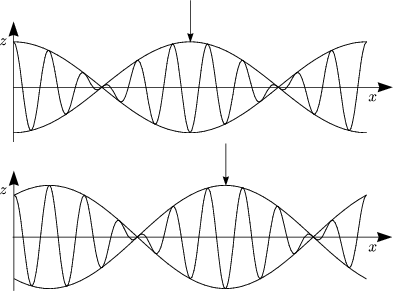
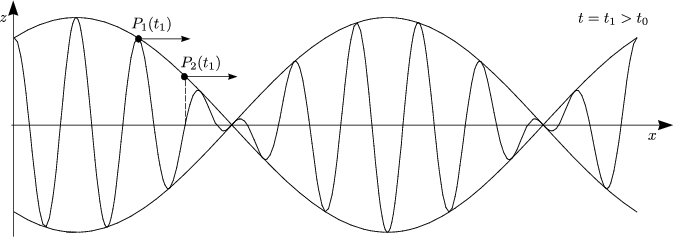
- Einfachster Fall: Gekoppeltes Federpendel
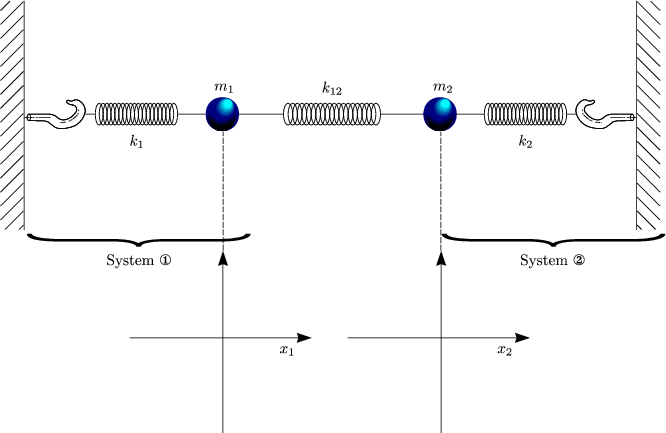
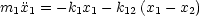
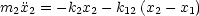
Es handelt sich um ein System aus gekoppelten Differentialgleichungen. Wir betrachten hierzu folgenden Spezialfall:
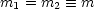
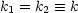
Damit folgt:

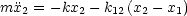
Durch Addition bzw. Subtraktion dieser beiden Differentialgleichungen ergibt sich nun folgendes System:

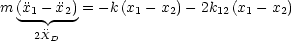
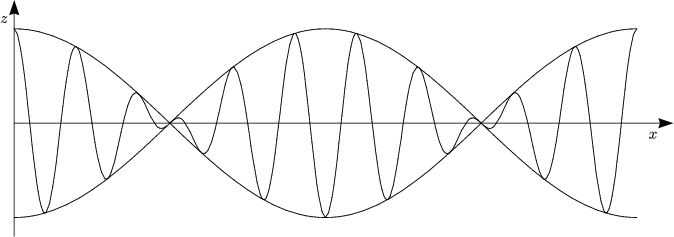
- Mittlere Auslenkung:
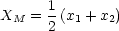
- Differenz:
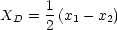
Damit erhalten wir also zwei Differentialgleichungen, die voneinander unabhängig sind:
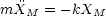
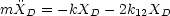
Hierbei folgt nun die Lösung:
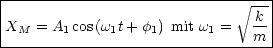
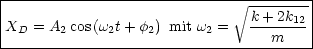
- Mittlere Auslenkung:
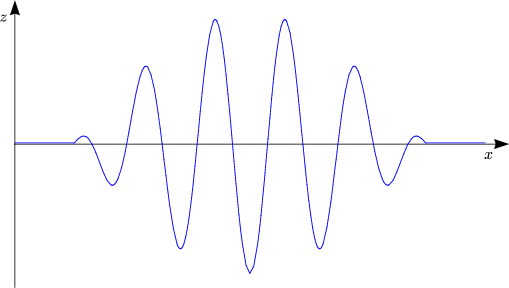
![x1(t) = XM-+-XD-=-A-[cos(w1t+-f1)+-cos(w2t+-f2)] =--------|
| (w1 - w2 f1- f2) (w1 + w2 f1 + f2)|
= |2A cos ---2---t+ ---2--- .cos --2---t+ --2---- |
---------------------------------------------------](ex1378x.gif)
![x2(t) = XM - XD = A [cos(w1t+ f1)- cos(w2t+ f2)] =
|-------(-----------------)----(-----------------)-|
= |-2A sin w1---w2t+ f1--f2- .sin w1 +-w2t + f1 +-f2|
------------2---------2------------2---------2------](ex1379x.gif)










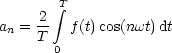
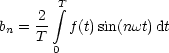
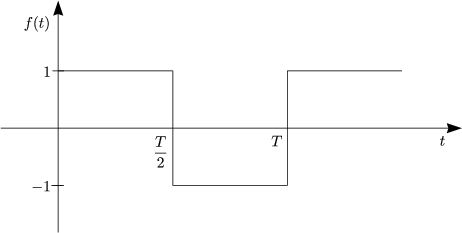
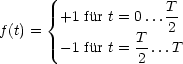
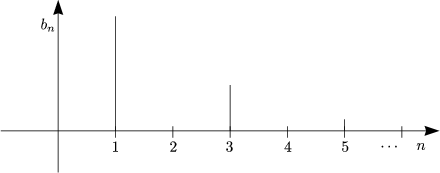
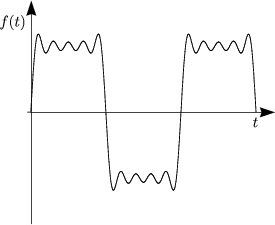
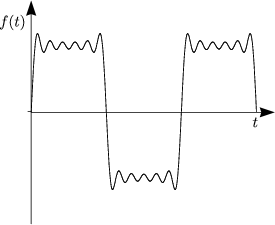
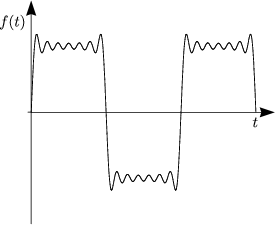
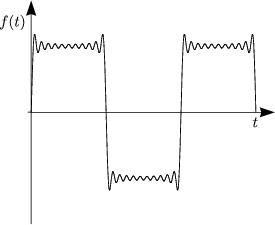
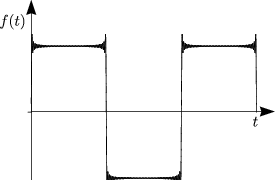
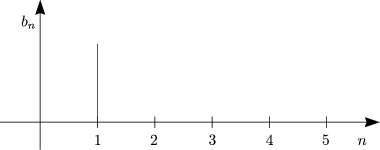
![( )
integral T2 T integral ( )
a = -2 cos(nwt) dt- cos(nwt)dt = -2-1- [sin nwt]T2- [sinnwt]TT =
n T T nw 0 2
0 T2
= -1-(sin np- sin 0- sin n.2p + sinnp) = 0 fur alle n
np ¨](ex1584x.gif)