1.3 Physikalische Gren/Einfhrung in die Vektorrechnung

1.3 Physikalische Größen/Einführung in die Vektorrechnung

Skalare:

Wie schwer ist etwas?
Angabe der Masse m
Wie lang ist etwas?
Angabe der Länge l
Wie komme ich nach München?
Die Angabe der Entfernung ( 200km) reicht NICHT! Man muß auch noch die Richtung wissen! Infolgedessen benötigt man Vektoren.

Vektoren:

Unter anderem können Verschiebungen durch Vektoren dargestellt werden. Außerdem werden beispielsweise folgende Größen durch Vektoren angegeben:

r

v

a

F

p

e

Addition:

Kommutativgesetz: + = +
Assoziativgesetz: + ( + ) = ( + ) +
Neutrales Element ( $/\ =$ Nullvektor): + = + =
Inverses Element: + (-) = - =

Unter der Identität versteht man einen Vektor mit gleicher Länge (BETRAG) und gleicher Richtung.

Zusammenfassung:

Vektoren im 2d: $( ) a =_ axc+ ayd =_ axex + ayey =_ [ax,ay] =_ ax ay$

Für den Betrag (Länge) eines Vektors im Zweidimensionalen ergibt sich:
$V~ -2---2- a = |a|= ax + ay$
Die Beträge der normierten Basisvektoren der Ebene ist gleich 1:
$|e |= |e |= 1 x y$
Für die Normierung eines allgemeinen Vektors ergibt sich:
$a0 = a-= 1 |a|$

$|a0|= |a|= 1 |a|$
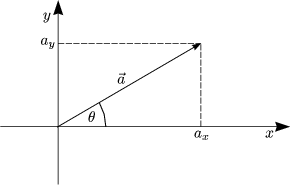
In Polarkoordinaten kann man die x- und y-Komponente eines Vektors folgendermaßen formulieren:
$a = acosh x$

$ay = asin h$

$( ) cosh a = |a| sinh$
Damit läßt sich der Vektor schreiben als:
$a = a cosh.ex + asinh .ey$
Bei Addition zweier Vektoren und addieren sich deren Komponenten einzeln:
$a + b = axex + ayey + bxex + byey = (ax + by)ex + (ay + by)ey$

$|| || V~ -------2----------2- |a + b| = (ax + bx) + (ay + by)$

$(ax + bx) a + b = ay + by$
Bei Multiplikation eines Vektors mit einer Konstante n werden die einzelnen Komponenten von mit n multipliziert.
$( ) n .a = nax nay$

$a+ b+ c+ d = (a + b + c + d )e + (a + b + c + d )e x x x x x y y y y y$
Vektoren im 3d:
Analog gilt dies für Vektoren im ³:
$V~ ----------- a = |a|= a2+ a2 +a2 x y z$

$a = axex + ayey + azez$

$a = [ax,ay,az]$

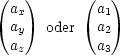
$( ) ( ) ax a1 ay oder a2 az a3$

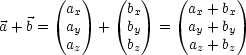
$( ) ( ) ( ) ax bx ax + bx a + b = ay + by = ay + by az bz az + bz$
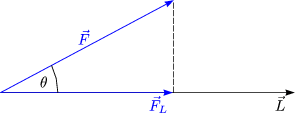
Für die S-Multiplikation (Skalar ^. Vektor) ergibt sich:
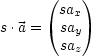
$( ) sax s.a = say saz$

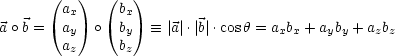
$(ax ) (bx) a o b = ay o by =_ |a|.|b|.cosh = a b + a b + a b az bz x x y y z z$

$a e .be +a e .b e +a e .b e +...+a e .b e = a b .e .e +a b .e .e +a b .e .e x x x x x x y y x x z z z z z z x x x -x y y y -y z z z z 1 1 1$
Produkte von Vektoren:
- Inneres Produkt o (Skalarprodukt) $|| || a o b = axbx + ayby + azbz = |a||b|cosf$
  Hieraus ergibt sich also ein Skalar.
  Kommutativgesetz:
  $a o b = b o a$
  
  Distributivgesetz:
  $ao (b + c) = ao b+ ao c$
  
  Orthogonalität:
  Wenn ab ist, gilt o = 0. Bei Gleichheit der Vektoren ( = ) erhalten wir: $|a| 2 = |a|.|a |.cos0 = |a|2 = a2$
- Äußeres Produkt × (Vektorprodukt)
  
  $a ×b =_ a.b.sinh.ea×b$
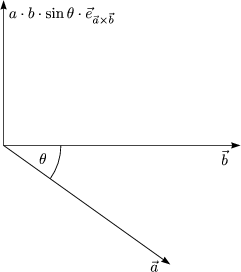
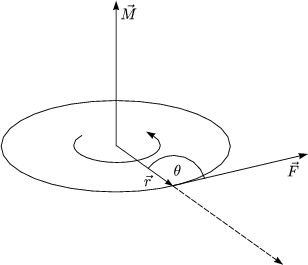
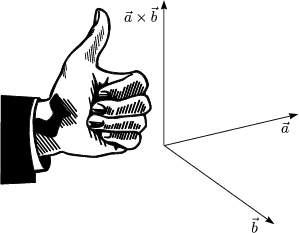
  Es ergibt sich also ein Vektor, der senkrecht sowohl auf als auch auf steht.
  $e _L a,b a×b$
Beispiel für Skalarprodukt:

$Arbeit=Kraft o Weg$

$W = F o L = |F|.|L |.cosf$

Beispiel für Vektorprodukt:
$Drehmoment=Radius × Kraft$

$M = r× F$

$|M |= |r ×F |= |r| .|F |sinf$