[next] [prev] [prev-tail] [tail] [up]

1.2 Messungen und Datenauswertung

Messung einer physikalischen Größe durch Instrumente, die Messwerte in Basiseinheiten wiedergeben. Die Genauigkeit ist begrenzt. Man unterscheidet zwischen 2 Fehlertypen (Unsicherheiten):

PIC Der Mittelwert einer gemessenen Größe x berechnet sich nach:

N <x> = x = 1-. sum x = 1(x +x + ...+ x ) N i=1 i N 1 2 N

1 N sum xw = lNim'--> oo N xi i=1

sx ist dabei ein Maß für die Breite:

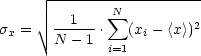
--------N---------- s = V~ --1---. sum (x - <x>)2 x N -1 i=1 i

Vertauschbarkeit: d(<x>) = V~ sx N

1.2.1 Zentraler Grenzwertsatz

Vertrauen von großer Anzahl von Zufallszahlen (Messungen):

V~ -1--- (x-2ms2)2- P(x;m;s) = 2ps e

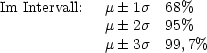
Im Intervall: m± 1s 68% m± 2s 95% m± 3s 99,7%

Mathematischer Einschub:
f = f(x1,x2,...,xN)

Die Ableitung -@f @xi = limDx'-->0( ) f(x1,x2,...,xi +-Dx,-...,xN)---f(x1,x2,...,xN) Dx heißt partielle Ableitung nach xi (analog xN).

Beispiel:
v(x,t) = x t

@v 1 @v x @x-= t; @t-= -t2

1.2.2 Fehlerfortpflanzung

Beispiel:
V~ -------------------- ( )2 ( )2 v = x; sv = @v- s2x + @v- s2t t @x @t

Es sei t = 15s, st = 0,5s, x = 100m und sx = 10cm. Damit ergibt sich:

m m v = 6,6s-± 0,2-s

Allgemein gilt:

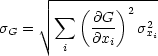
------------- s um ( )2 sG = V~ @G- s2xi i @xi

Statistischer und systematischer Fehler werden getrennt behandelt. Die Alternative ist folgende einfachere Rechnung (Größtfehler-Addition).

f(x+ Dx, y+ Dy, z + Dz)

Das 1.Glied der mehrdimensionalen TAYLOR-Entwicklung lautet:

| | | | | | ||@f|| ||@f-|| ||@f-|| Df = |@x|Dx + |@y |Dy + |@z|Dz

Beispiel:
a b c R = x y z

@R- a-1 bc @R- b b- 1c @x = ax yz ; @y = x y z

Damit folgt:

| | | | | | DR = ||aR-||Dx + ||bR-||Dy + ||c R||Dz | x | | y| | z|

Für den relativen Fehler ergibt sich:

DR--= |a|Dx-+ |b|Dy-+ |c| Dz R x y z

Darstellung:
Wert=(Bestwert± Unsicherheit) .Ma ßeinheit

Signifikante Stelle:

m g = (9,82± 0,02)2 s

g = (9,8± 0,2)m s2

[next] [prev] [prev-tail] [front] [up]