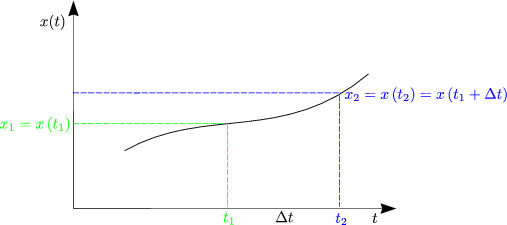
- Geschwindigkeit
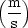 :
:
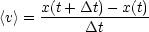
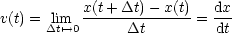
Umgekehrt folgt:
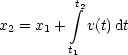
- Beschleunigung
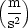 :
:
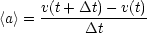
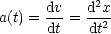
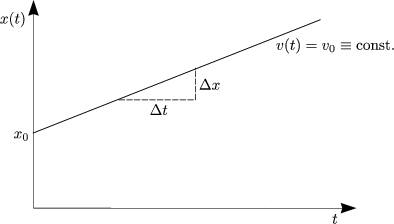
Unbeschleunigte Bewegung: a(t) = 0
Beispiel: Fallender Stein:


Umgekehrt folgt:
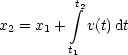
Unbeschleunigte Bewegung: a(t) = 0


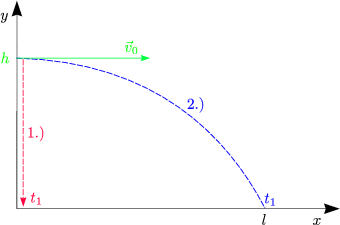

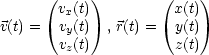
Auch hier ist die Bewegung in x, y, z-Richtung unabhängig!

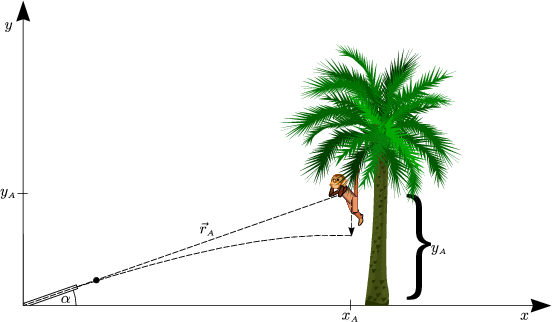
Für t = tA trifft die Kugel den Affen:
Es gilt somit:
Damit folgt:
Dies ist eine wahre Aussage. Der Affe ist wohl kein guter Physiker, da er von der Kugel getroffen wird.
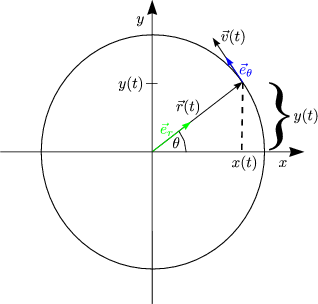
![]() (t),
(t), ![]() (t),
(t), ![]() (t) ändern sich laufend!
(t) ändern sich laufend!
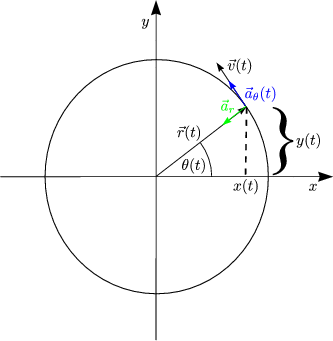
Mit der Umlaufzeit T folgt:
Damit ergibt sich:
Zentripetalbeschleunigung (Tangentialbeschleunigung=0)

Dies entspricht der Umlaufzeit eines Satelliten im erdnahen Orbit.