|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
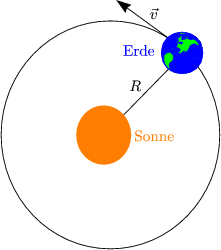
Kraft zwischen Sonne und Erde (mE = 6 . 1024 kg):
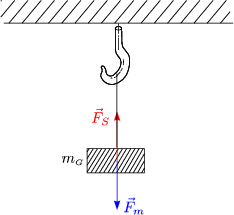
Da sich der Körper im Kräftegleichgewicht befindet, ist die Vektorsumme aller Kräfte gleich 0:
Die einzigen Kräfte, die auftreten, sind die Gewichtskraft und die Seilkraft. Die Summe aller Kräfte am ruhenden Körper ist gleich Null:
Damit folgt:
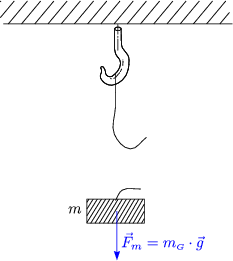
![]() Träge und schwere Masse sind identisch!
Träge und schwere Masse sind identisch!
![]() Äquivalenzprinzip!
Äquivalenzprinzip!

Die allgemeine Betrachtung liefert:
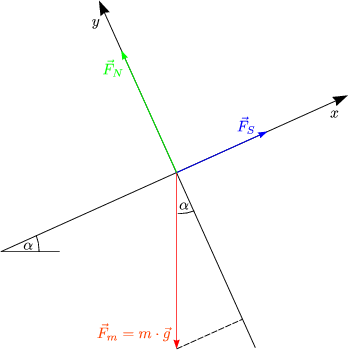
Die Kräfte werden komponentenweise betrachtet:
Dann ergibt sich folgende Lösung:


Vektoriell geschrieben lautet die Kräftebilanz:
Wir betrachten nun die Kräfte komponentenweise und erhalten somit:
Die beiden Körper erfahren die gleiche Beschleunigung, außerdem sind die beiden Seilkräfte gleich groß.

Die Kräfte in vertikaler Richtung, also die und die gleichen sich aus. Infolgedessen sind nur noch die waagerechten Kräfte von Bedeutung. Wir addieren die drei Gleichungen und erhalten so
Für die anderen Seilkräfte folgt:
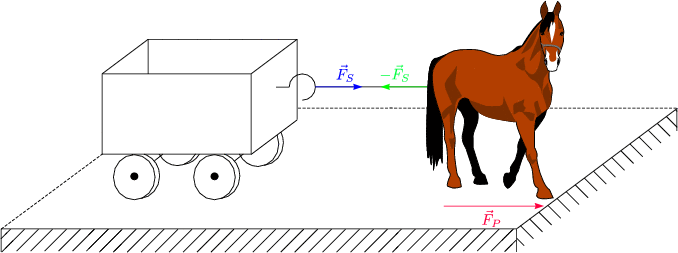
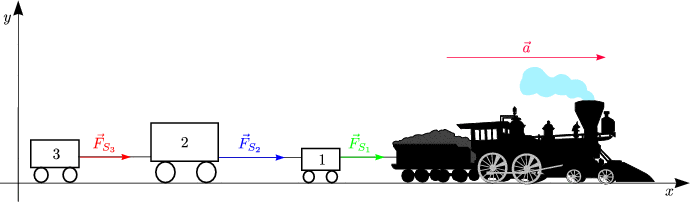
Für das Pferd gilt folgendes:
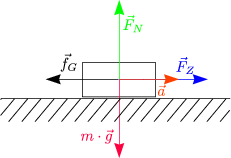
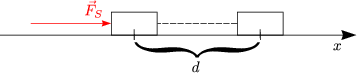
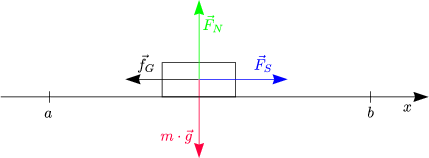
Welche Kräfte wirken auf die Klötze?
Die Schubkraft ![]() wirkt auf das ganze System bestehend aus den beiden
Klötzen.
wirkt auf das ganze System bestehend aus den beiden
Klötzen.
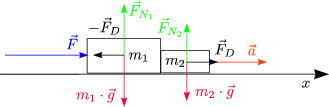
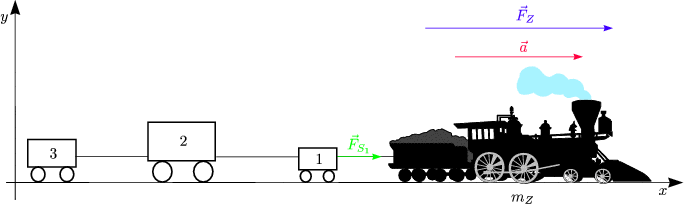
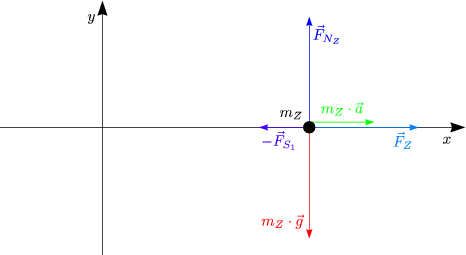
Die Kräftebilanz für das gesamte System lautet:
Speziell für den Klotz 2 erhalten wir:
Die relevanten Komponenten sind diejenigen in x-Richtung:
Damit ergibt sich also:
Diese Kraft ist gleich der Kraft ![]() 2x, mit welcher der zweite Klotz
beschleunigt wird.
2x, mit welcher der zweite Klotz
beschleunigt wird.
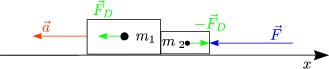
Damit ergibt sich für die Kraft ![]() Dx auf den ersten Klotz:
Dx auf den ersten Klotz:
Damit gilt also:
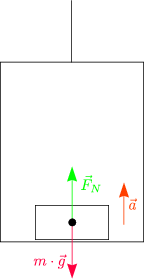
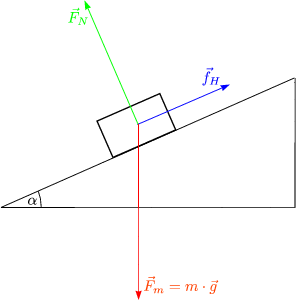
| F = m . g | 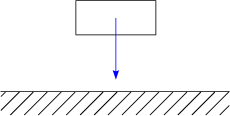 | Gravitationskraft | |
| F = FN | 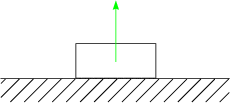 | Normalkraft | |
| F = FZ |  | Zugkraft | |
| F = FD |  | Schubkraft | |
Bis jetzt waren Kräfte konstant. Damit galt die Bewegungsgleichung:
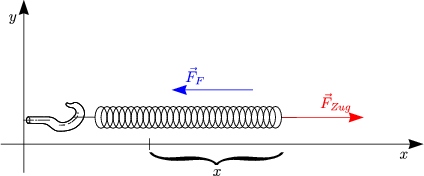
Als Beispiel für eine Kraft, die nicht konstant ist, wollen wir die Federkraft näher betrachten:
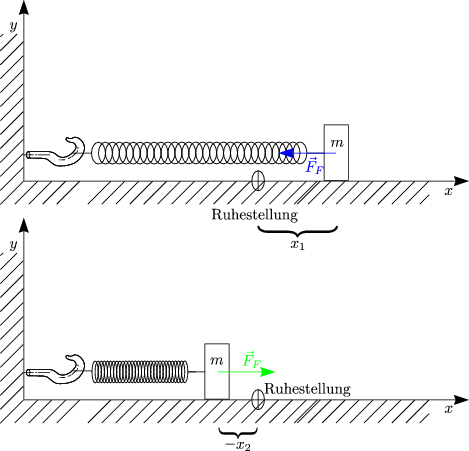
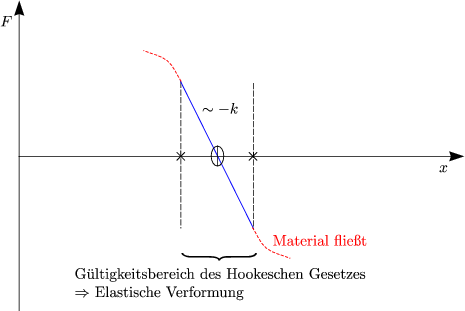
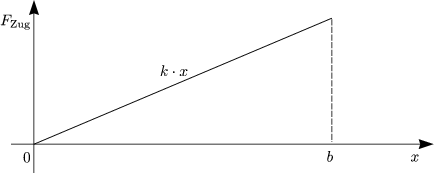
Das sogenannte Hookesche Gesetz lautet:
Es ergibt sich folgende Beschleunigung:

Wir verwenden zur Lösung folgenden Ansatz:
Wir setzen dies in die Gleichung ein:
Wir haben folgende Randbedingungen:
|
| (2.1) |
Die Lösung lautet dann:
Aus ![]() = 2
= 2![]()
![]() =
= ![]() folgt:
folgt:
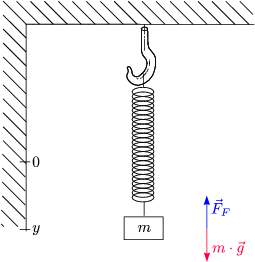
Betrachten wir die y-Komponente:
Damit ergibt sich:
Damit folgt das Gewicht des Massestücks:
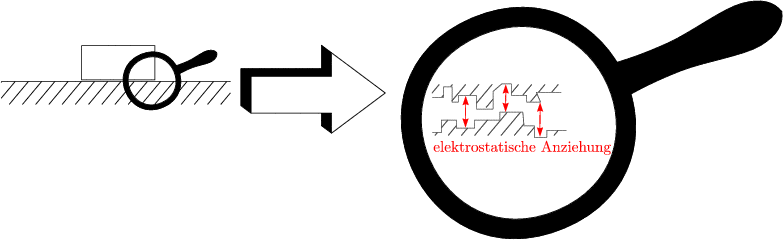
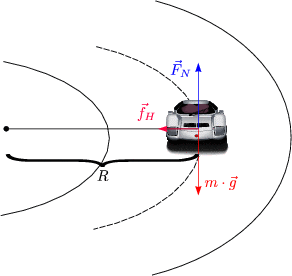
Verklebung zweier Körper durch Rauhigkeit oder elektrostatische Kräfte
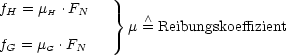
Allgemein gilt ![]() H >
H > ![]() G.
G.
Betrachten wir außerdem folgenden Sonderfall:
Für ![]() = -
= -![]() G gleitet der Körper mit konstanter Geschwindigkeit.
G gleitet der Körper mit konstanter Geschwindigkeit.
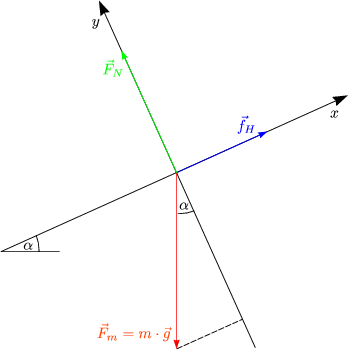
Mit fH = FN . ![]() H und
H und ![]() H = tan
H = tan![]() , wobei
, wobei ![]() der maximal mögliche Wert
ist (bevor m gleitet).
der maximal mögliche Wert
ist (bevor m gleitet).
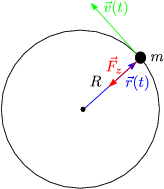
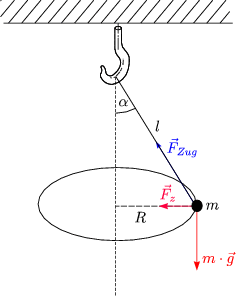
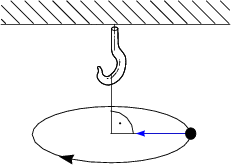
Es wirkt die Zentripetalkraft:
Es gilt für die Beschleunigung:
Damit folgt dann für die Bewegungsgleichung:
Durch zweimalige Integration nach t erhalten wir ![]() (t):
(t):
Mit |![]() z| =
z| = ![]() 2R =
2R = ![]() resultiert:
resultiert:
Damit folgt also schließlich:
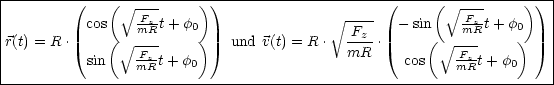
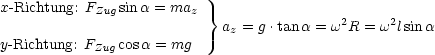
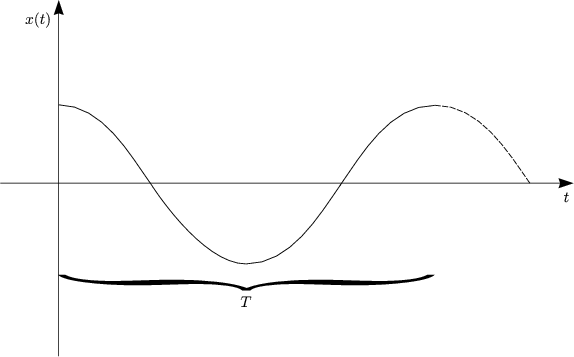
Hiermit folgt für die Kreisfrequenz ![]() und der Periodendauer T:
und der Periodendauer T:
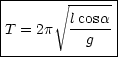
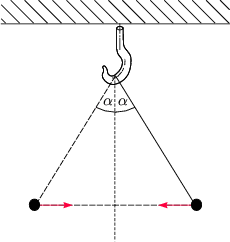

Betrachten wir folgendes Zahlenbeispiel:
|
| (2.2) |

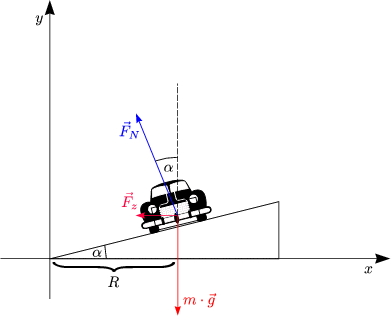
Damit ergibt sich folgender Winkel:
Damit folgt für die Geschwindigkeit:
Solange v <![]() rutscht das Auto nicht! Wenn v >
rutscht das Auto nicht! Wenn v > ![]() beginnt
es zu rutschen!
beginnt
es zu rutschen!
(Oder seit Adam und Eva das Paradies verlassen mußten)

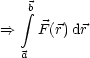
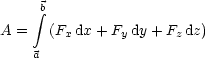
![2
[A] = 1kg m- =_ 1Nm
s2
=_ 1Joule
=_ 1Ws](ex430x.gif) | (2.3) |
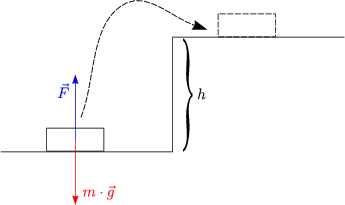
Professor MÜLLER steigt die Stufe hinauf:
Mit dieser Arbeit kann man eine 40W-Glühbirne 10s leuchten lassen!
Kraft, die Arbeit leistet:
|
|
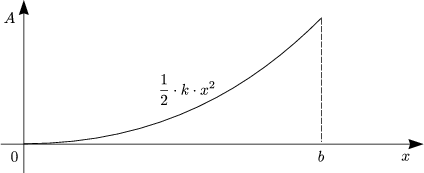
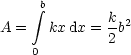
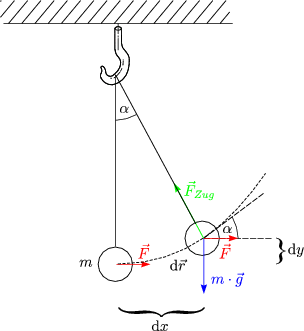
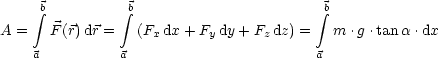
Mit tan![]() =
= ![]() folgt:
folgt:

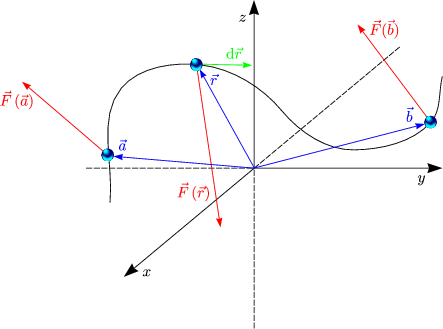
Die Arbeit in konservativen Kraftfeldern ist unabhängig vom Weg:
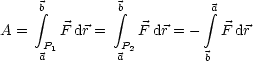

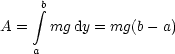
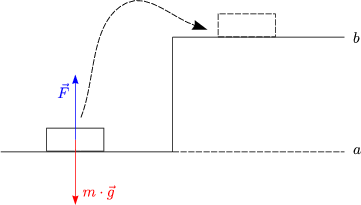
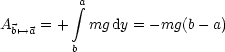
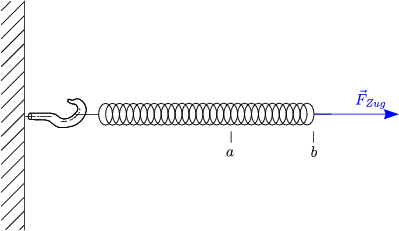
Für die Zugkraft ergibt sich:
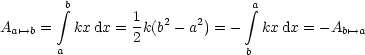

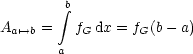

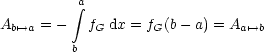
Das heißt:
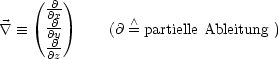
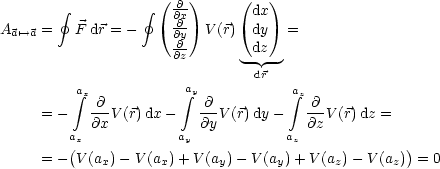 | (2.4) |
Wenn resultierende Kraft Arbeit leistet (![]() = m
= m![]() ), bekommt das Objekt
kinetische Energie:
), bekommt das Objekt
kinetische Energie:
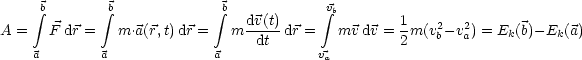
Potentielle Energie ist gespeicherte Energie, die vollständig umgewandelt werden kann in kinetische Energie.
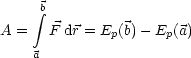
Die Summe aller Energien in einem abgeschlossenen System ist konstant. (Spezialfall: reibungslose mechanische Energie)
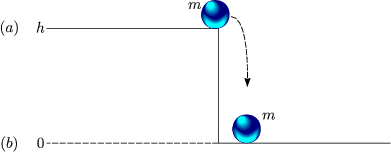
Damit ergibt sich folgende Geschwindigkeit:
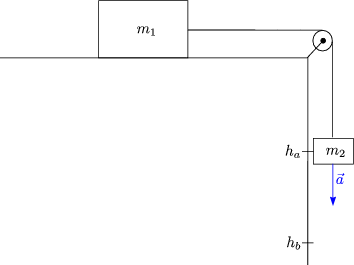
Hiermit folgt:
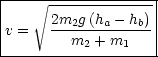
Betrachten wir wiederum folgendes Zahlenbeispiel:
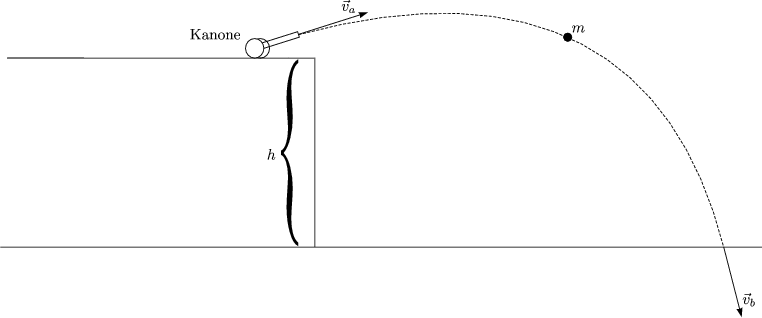
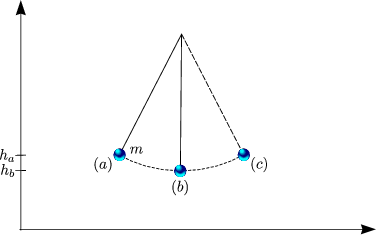

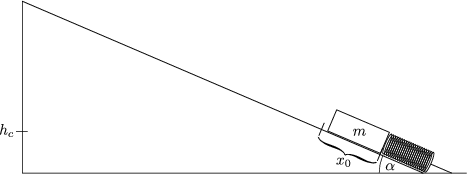
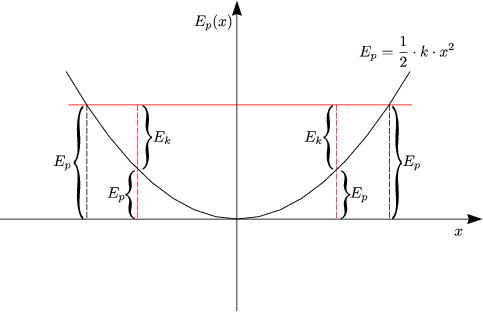

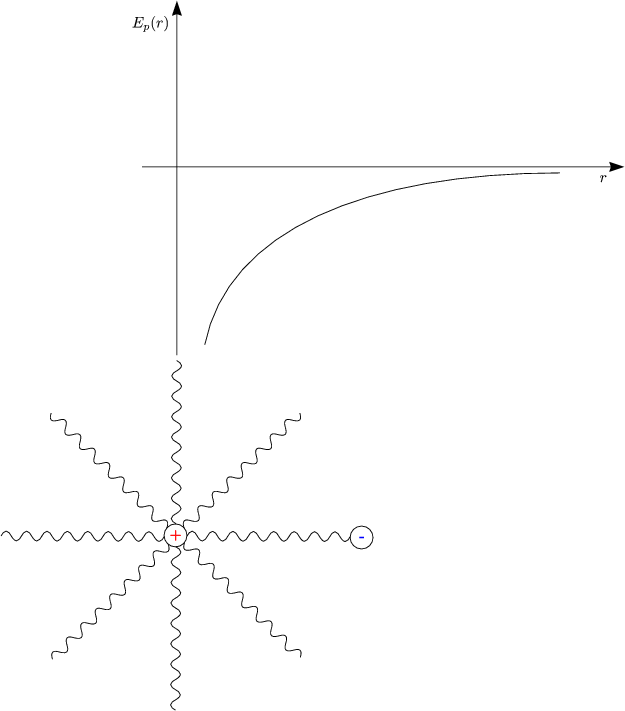
Es galten die Gesetze der Erhaltung mechanischer Energie, d.h. wir verzichteten auf dissipative Kräfte.
Die innere Energie ist eine Art Arbeit, welche nicht vollständig in kinetische Energie (im allgemeinen mechanische Arbeit) zurückgewandelt werden kann.
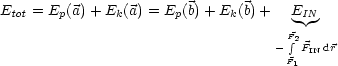
Hiermit folgt:
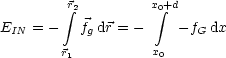
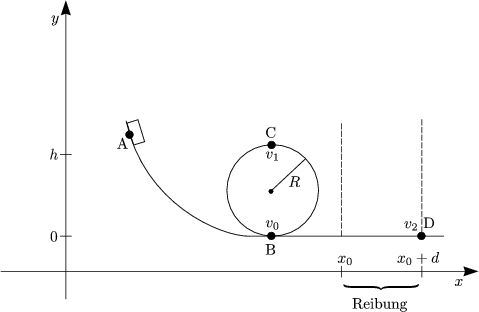
|
||||||
|
||||||
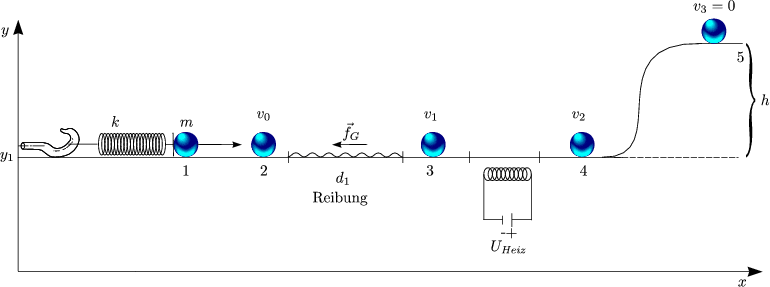
Zu jedem Zeitpunkt (Ort) kann man somit die Bewegung beschreiben.
| RECHNEN MIT ENERGIEN IST HÄUFIG EINFACHER ALS MIT BEWEGUNGSGLEICHUNGEN ODER KRÄFTEN! |
Nach JAMES WATT (*1736): Entwickler der modernen Dampfmaschine (Auch 1PS = 735,4988W)
Wir bestimmen die Leistung des Übungsgruppenleiters, Höhe: 3m
Eine Lampe besitzt beispielsweise eine Leistung von 50 - 100W. Für einen Porsche gilt:
Bis jetzt haben wir Körper nur im geschlossenen System betrachtet. Jetzt wollen wir makroskopische Systeme, in denen N Teilchen miteinander wechselwirken, untersuchen. Unser Interesse gilt der Gesamtbewegung des Systems.

Unsere Milchstraße besteht aus ungefähr 1010 Sonnen. Jeder Stern hat Eigenbewegung und außerdem bewegt sich das ganze. Also definieren wir:
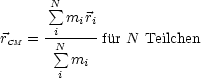
![]() CM ist der massegewichtete Mittelwert der Ortsvektoren.
CM ist der massegewichtete Mittelwert der Ortsvektoren.
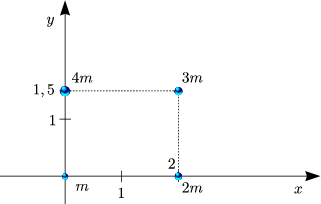
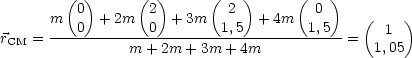
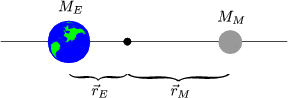
Betrachten wir folgendes Zahlenbeispiel:
![]() =
= ![]() . m gilt sowohl für Vielteilchensysteme als auch für massive Körper.
. m gilt sowohl für Vielteilchensysteme als auch für massive Körper.

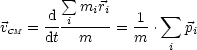
Analog gilt dies für die Beschleunigung.
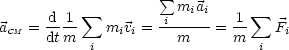
Das Gesetz der Impulserhaltung folgt direkt aus NEWTON.
| Wenn keine externen Kräfte vorhanden sind, ist die Summe aller Momente im geschlossenen System konstant |
Da es keine äußeren Kräfte gibt, ist ![]() CM erhalten.
CM erhalten.