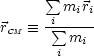
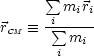
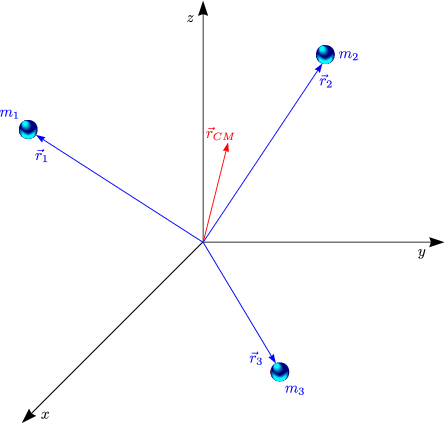
Für unendlich viele Teilchen kann man dies verallgemeinern:
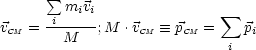
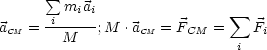
In einem geschlossenen System ohne resultierende (externe) Kraft ist der Gesamtimpuls
erhalten:
|
||||||
Wenn keine äußeren Kräfte wirken,
ist ![]() CM erhalten. ODER: WIE ERFAHRE ICH DAS GEWICHT MEINES
ÜBUNGSGRUPPENLEITERS? (funktioniert auch bei Frauen!)
CM erhalten. ODER: WIE ERFAHRE ICH DAS GEWICHT MEINES
ÜBUNGSGRUPPENLEITERS? (funktioniert auch bei Frauen!)
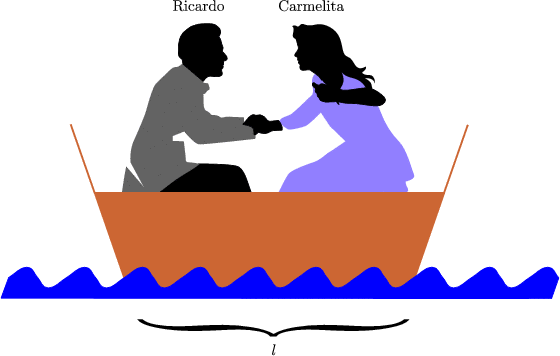
Die beiden tauschen die Plätze. Dabei bewegt sich das Boot um 40 cm.
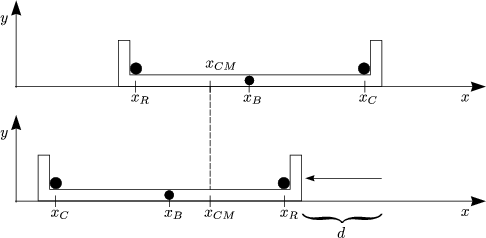
Auch gilt xC = xR + l und mit d = 0,40m folgt:

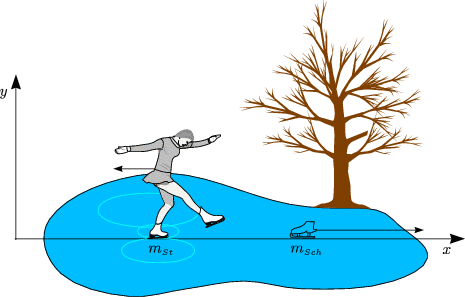
Keine resultierenden äußeren Kräfte:
Hier gilt ![]() CM =
CM = ![]() = mSt
= mSt![]() St + mSch
St + mSch![]() Sch. Wir betrachten die Bewegung in
x-Richtung:
Sch. Wir betrachten die Bewegung in
x-Richtung:
CM-Bewegung mit externer Kraft:
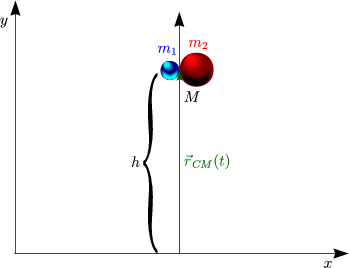
Betrachte Fall der Kugeln:
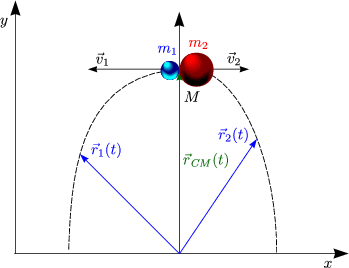
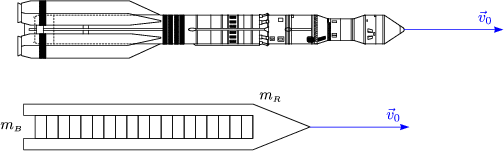
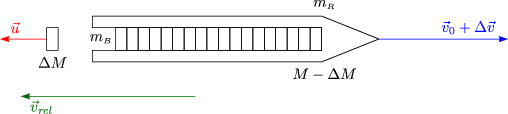
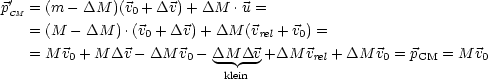 | (2.5) |
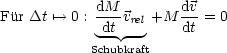
Wir zerlegen dies in Komponenten:
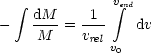
Damit ergibt sich dann für die Endgeschwindigkeit:

Der Brennstoff dieser Rakete besteht aus Kerosin und flüssigem Sauerstoff (O2(l)).
Die Brenndauer des Treibstoffs beträgt 100 s. Unter Vernachlässigung der Gravitation ergibt sich eine Endgeschwindigkeit von:
Korrekt ist jedoch:
Dies ist viel zu wenig! Die Lösung dieses Dilemmas ist nun die Mehrstufenrakete, bei welcher im Laufe des Flugs mR reduziert wird!
Damit gilt:
Für vend = c ergibt sich eine Masse des Brennstoffs von 104912 kg! Dies geht nicht!
Geht auch nicht!
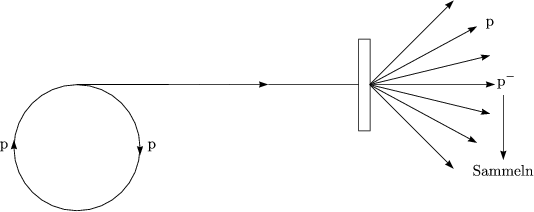

Muß mitgenommen werden zum Bremsen:
Allerdings wurde bislang nur ca. 0,1 mg an p hergestellt!
Kinetische Energie vor und nach dem Stoß sind gleich:
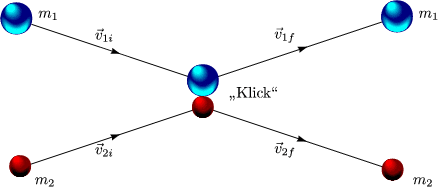
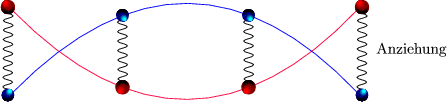
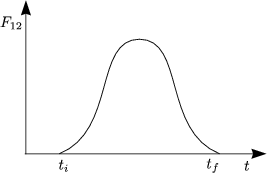
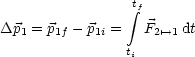
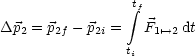
Aus dem 3.Newtonschen Gesetz ![]() 21 = -
21 = -![]() 12 ergibt sich
12 ergibt sich ![]()
![]() 1 +
1 + ![]()
![]() 2 =
2 = ![]() und
damit:
und
damit:
Dies ist nichts anderes als der Impulserhaltungssatz.
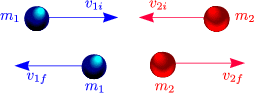
Einsetzen ergibt:
| v1f = v2i |
| v2f = v1i |
| v1f = 0 |
| v2f = v1i |
| v1f = -v1i + |
| v2f = 0 |
| v1f = v1i |
| v2f = 2v1i |
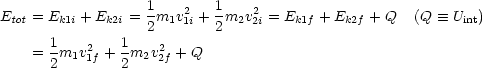 | (2.6) |
Eindimensional, total inelastisch:
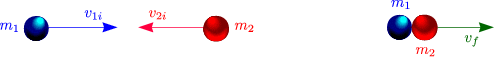
Der Impuls ist erhalten:
Man hat ![]() -Zerfälle untersucht:
-Zerfälle untersucht:
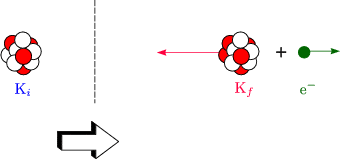
Hierbei wurde festgestellt, daß ![]() Ki >
Ki > ![]() Kf +
Kf + ![]() e-. Die Lösung des Problems ist nun
folgende:
e-. Die Lösung des Problems ist nun
folgende:
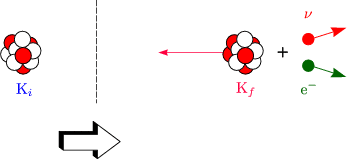
Für die Energie bei einem total inelastischen Zusammenstoß gilt jedoch:
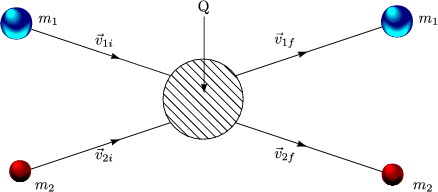
Aus der Bewegung am Anfang und am Ende kann man Rückschlüsse über den Stoßprozess ziehen.

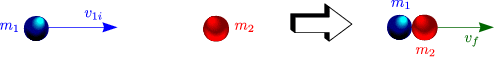
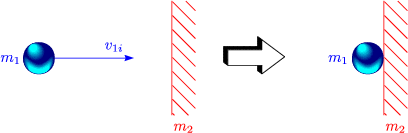
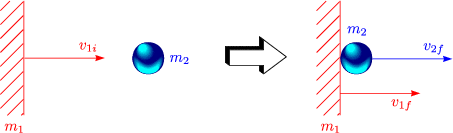
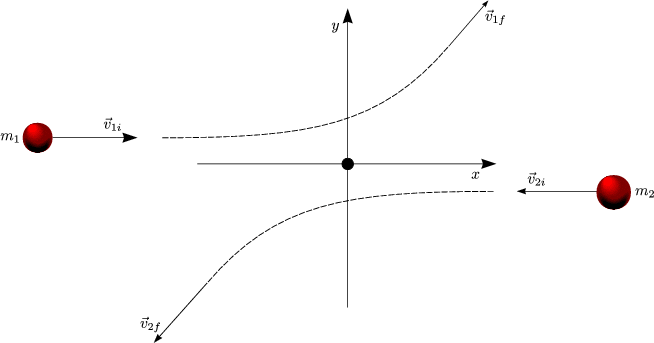
Der Beobachter ruht im m2
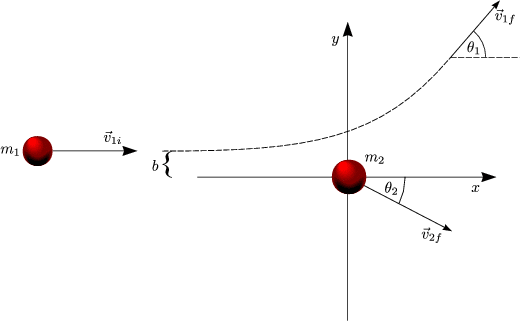
b ist der sogenannte Impaktparameter.
In Komponenten läßt sich dies schreiben als:
Es ergeben sich 3 Gleichungen. Wenn die Anfangsbedingungen bekannt sind, bleiben 2 Unbekannte.
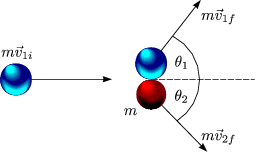
Wenn man diese beiden Bedingungen gleichsetzt, folgt: