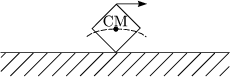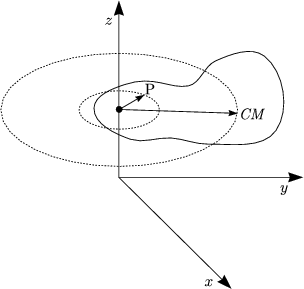
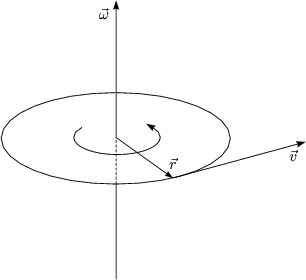
Jeder Punkt P dreht sich im Kreis mit gleichem Zentrum und gleicher
Winkelgeschwindigkeit ![]() . Von oben betrachtet:
. Von oben betrachtet:
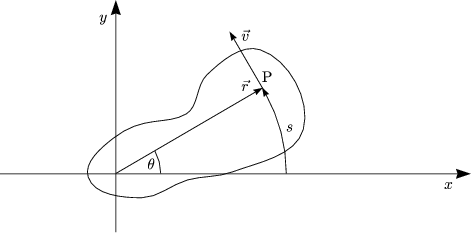
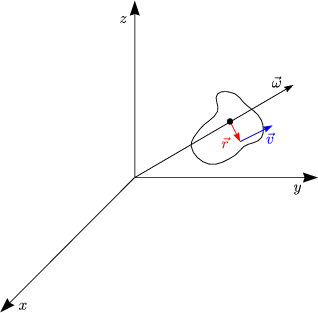
Für die Bewegungsgleichungen folgt:
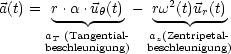
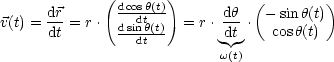
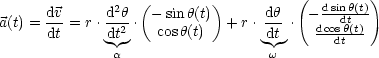
Insbesondere gilt:
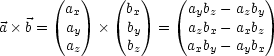
Ein Beispiel aus der Kinematik ist ![]() =
= ![]() ×
×![]() .
.
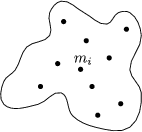
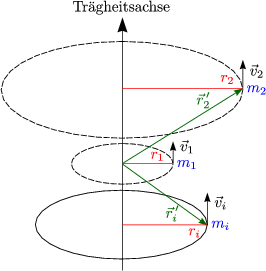
Zu jedem Zeitpunkt gilt:
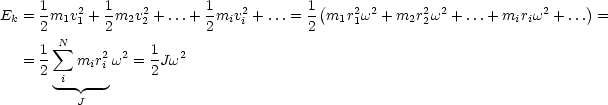 | (2.7) |
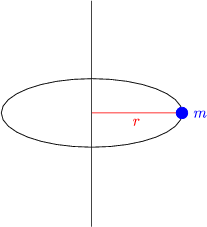
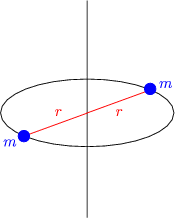
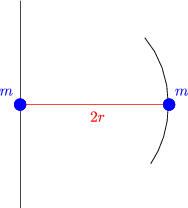
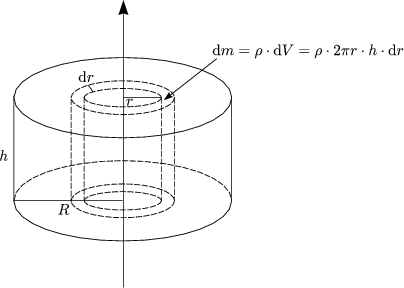
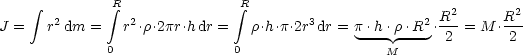
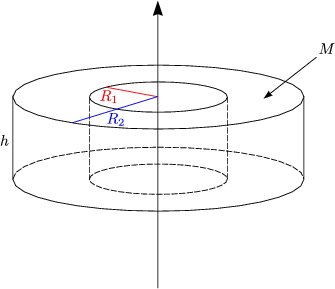
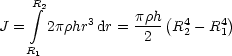
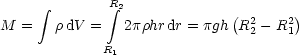
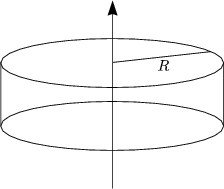
Generell gilt J = ![]() . M . R2.
. M . R2.
Der Impuls berechnet sich nach ![]() = m
= m![]() und für den Drehimpuls gilt
und für den Drehimpuls gilt ![]() = J .
= J .![]() .
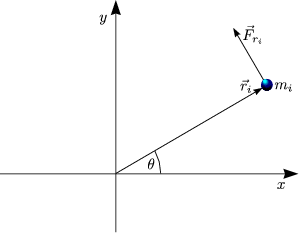
Für ein Vielteilchensystem folgt außerdem:
.
Für ein Vielteilchensystem folgt außerdem:
Impuls und Drehimpuls sind erhalten ohne Einwirkung äußerer Kräfte, denn es gilt:

Eine Person halte zwei Kugeln mit jeweils m = 2kg im Abstand ra =
0,8m vom Körper weg und drehe sich mit der Winkelgeschwindigkeit
![]() = 3
= 3![]() um ihre eigene Achse. Wir betrachten die Person
näherungsweise als Zylinder der Masse M = 50kg und Radius
R = 0,14m. Die Kugeln werden aufgrund ihrer verhältnismäßig
geringen Größe als Massepunkte behandelt. Damit ergibt sich für das
Trägheitsmoment des Systems bestehend aus Kugeln und Person:
um ihre eigene Achse. Wir betrachten die Person
näherungsweise als Zylinder der Masse M = 50kg und Radius
R = 0,14m. Die Kugeln werden aufgrund ihrer verhältnismäßig
geringen Größe als Massepunkte behandelt. Damit ergibt sich für das
Trägheitsmoment des Systems bestehend aus Kugeln und Person:
Für den Drehimpuls folgt:
Wir erhalten daraus die Periodendauer T:
Nun werde der Abstand der Kugeln auf rb = 0,2m verkleinert, indem die Person die Arme an den Körper heranzieht. Damit ergibt sich:
Aufgrund der Erhaltung des Drehimpulses L gilt:
Die Person dreht sich also schneller als vorher.
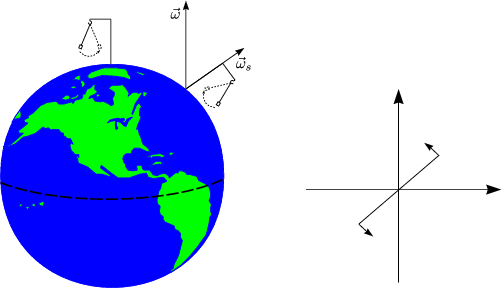
In Karlsruhe gilt ![]() s
s ![]() 28h.
28h.

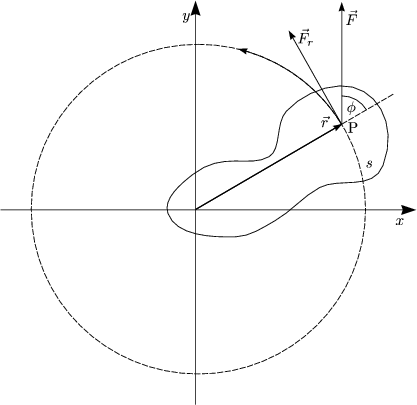
Es ist M = 0, wenn ![]() = 0 gilt.
= 0 gilt.
![]() =
= ![]() ist die Winkelbeschleunigung.
ist die Winkelbeschleunigung.
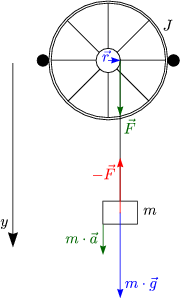
Daraus folgt durch die Zerlegung in Komponenten:
Auch gilt ![]() =
= ![]() und somit haben wir:
und somit haben wir:
Wir führen einen Check mit Extremfällen durch:
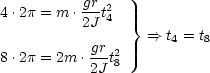
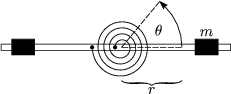
Es gilt das Hookesche Gesetz:
Wir verwenden folgenden Ansatz
Durch Einsetzen folgt:
| Lineare Arbeit: | | Rotationsarbeit: | |
| A = | 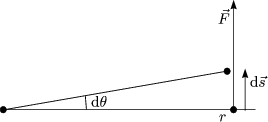 | ||
| dA = | |||
| A = | |||
Für resultierende Drehmomente:
Allgemein gilt:

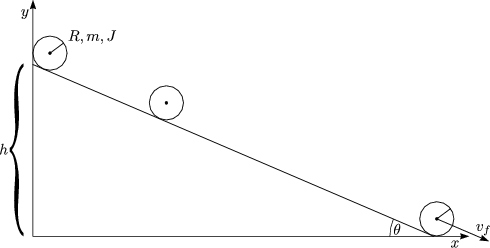
Wie hängen v und ![]() zusammen? Mit
zusammen? Mit ![]() =
= ![]() erhält man die
Geschwindigkeit am niedrigsten Punkt:
erhält man die
Geschwindigkeit am niedrigsten Punkt:
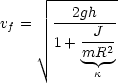
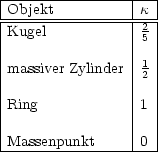
Für runde Objekte gilt J = ![]() . mR2.
. mR2. ![]() lautet für folgende spezielle
geometrische Objekte:
lautet für folgende spezielle
geometrische Objekte:
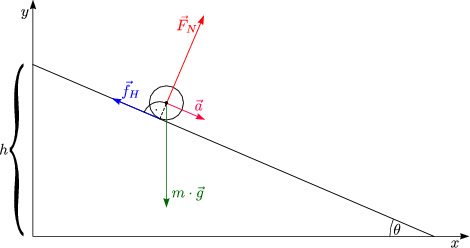
Betrachten wir das ganzen in Komponenten:
Es liegt eine kombinierte Bewegung vor: ![]() =
= ![]() .
.
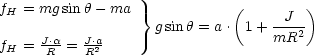
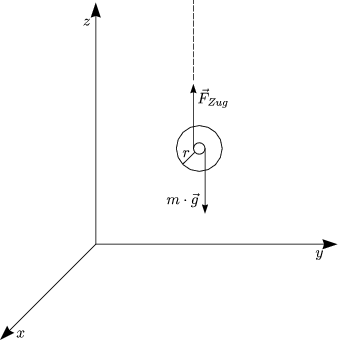
In Komponenten zerlegen:
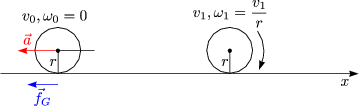
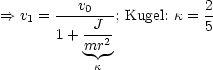
Unabhängigkeit von Reibungskraft!
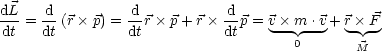
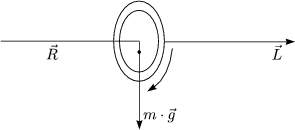
Was ist J? ![]() ist nicht notwendig parallel zu
ist nicht notwendig parallel zu ![]() !
!

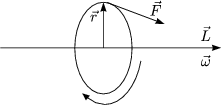
Es gilt:
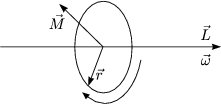
Die sogenannte Präzessionsfrequenz errechnet sich nach:
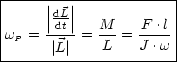

Bis zu welchem Winkel ![]() min ist die Leiter stabil? Wir betrachten hierzu die
Kräfte:
min ist die Leiter stabil? Wir betrachten hierzu die
Kräfte:
Betrachte Drehmomente (um Fußpunkt der Leiter):
Wir zerlegen in Komponenten:
Die Leiter steht stabil bis zum Winkel ![]() min:
min:
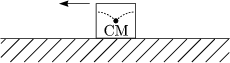
Das Gleichgewicht ist neutral, wenn bei kleiner Drehung des Objektes der Schwerpunkt auf gleicher Höhe bleibt.
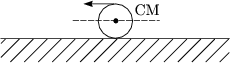
Das Gleichgewicht ist labil, wenn der Schwerpunkt bei kleiner Drehung absinkt (metastabil).