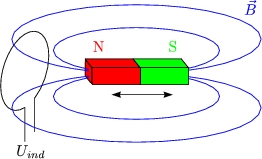
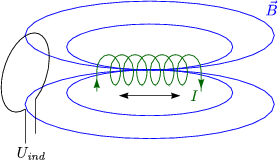
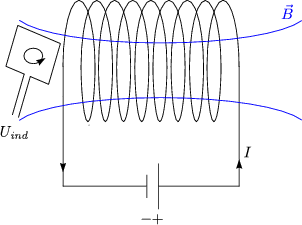
Die Versuche von FARADAY (1831) haben gezeigt, da die zeitliche Vernderung eines Magnetfeldes (besser: magnetischen Flusses) Strme in einem Leiter induzieren.



Ein zeitlich vernderlicher Flu erzeugt ein elektrisches Feld. Mit ![]() m =
m = ![]() A
A![]() d
d![]() folgt
das Induktionsgesetz:
folgt
das Induktionsgesetz:
| Die LENZsche Regel: |
| Die Induktionsspannung und der Strom, den diese hervorruft, sind stets so gerichtet, da sie ihrer Ursache entgegenwirken. |
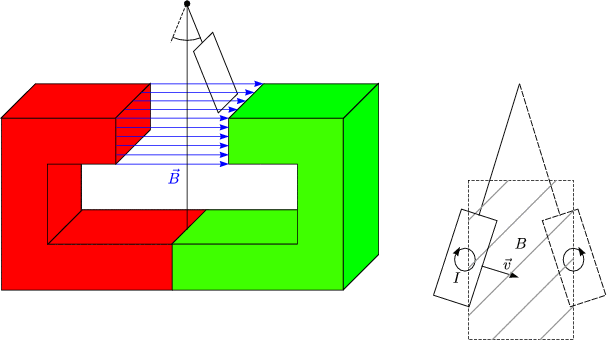
Bewegung einer Schleife im ![]() -Feld:
-Feld:
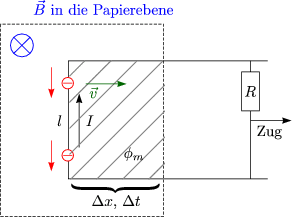
Die Elektronen werden durch die LORENTZkraft zu einem Strom beschleunigt. Die LORENTZkraft entspricht einer effektiven elektrostatischen Kraft:
Der magnetische Flu ![]() m folgt aus der allgemeinen Beziehung:
m folgt aus der allgemeinen Beziehung:
Damit folgt:
Das Minuszeichen kommt daher, weil der Flu abnimmt.
Wegen des Innenwiderstands wird I verringert, so da ![]() kleiner wird.
kleiner wird.
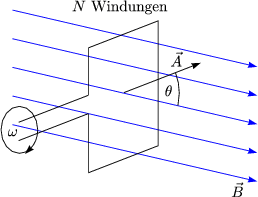
Somit folgt fr die induzierte Spannung:
Dieses Prinzip wird bei der Wechselspannungserzeugung eingesetzt.
Mit dem STOKESschen Satz ergibt sich dann:
Damit ergibt sich:
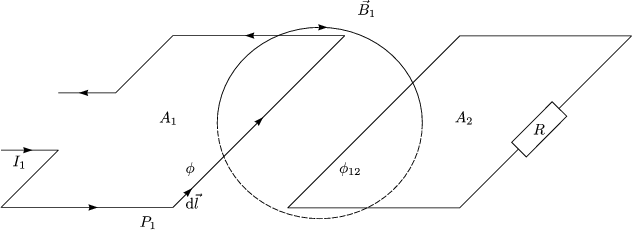
Wir fhren die Induktivitt L als Gre ein. Diese hat folgende Einheit:
Mit ![]() 12 =
12 = ![]() A2
A2![]() 1 d
1 d![]() 2 =
2 = ![]() A2
A2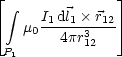 d
d![]() 2 erhalten wir fr die
Induktivitt:
2 erhalten wir fr die
Induktivitt:
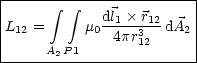
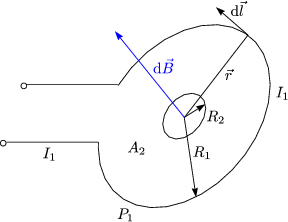
Fr R1 » R2 gilt r12 = r. Dann erhlt man fr den Flu:
Damit gilt schlielich fr die Induktivitt:
Fr I1 = I1(t) gilt:
Daraus folgt die Induktivitt:
Wir erhalten also folgenden sehr wichtigen Zusammenhang zwischen der zeitlichen nderung des Flusses und des elektrischen Stromes:
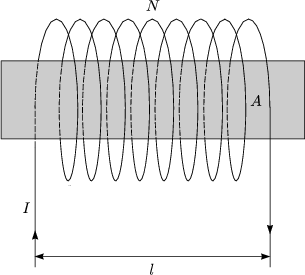
Dies ist die sogenannte Selbstinduktivitt einer Spule. Allgemein gilt:
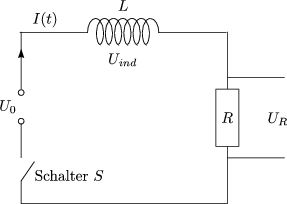
Mittels der Maschenregel folgt:
Wir erhalten also folgende Differentialgleichung:
Die Lsung erhalten wir mit folgendem Ansatz:
Durch Einsetzen resultiert dann fr den zeitlichen Verlauf des Stroms:

Wir veranschaulichen das Verhalten graphisch:
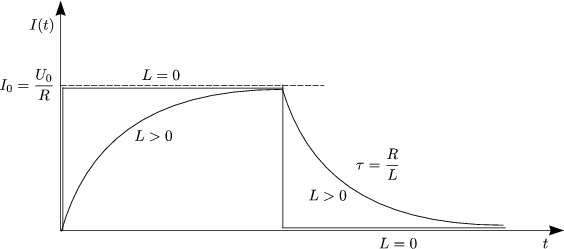
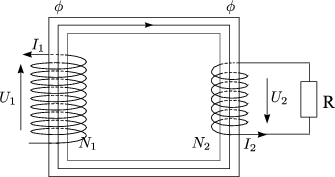
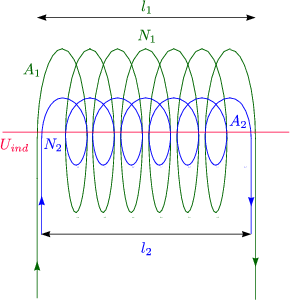
Es ergibt sich folgender wichtiger Zusammenhang zwischen den Windungszahlen und der Spannungen:
Die Spannungen verhalten sich also genauso wie die Windungszahlen. (Das --Zeichen bei gleichem Wicklungssinn der Spulen)
Damit resultiert: