5.2 MAXWELLscher Verschiebungsstrom

Wir betrachten das Magnetfeld bei der Entladung eines Kondensators:

A₁ und A₂ seien von P umrandet. Es gilt das Ampèresche Gesetz:

Durch die Flche A₁ fliet ein elektrischer Strom I, womit gilt:

Der Strom durch die Flche A₂ ist gleich Null:

Es handelt sich somit um einen Widerspruch! MAXWELL lste das Problem durch Einfhrung eines effektiven Stromes, des sogenannten Verschiebungsstroms:

Fr die MAXWELLsche Gleichung gilt also:

Mit dem STOKESschen Satz erhalten wir:

Mit ₀ ^. ₀ = folgt:

Da > 0, gilt schlielich:

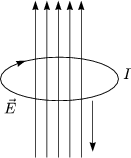
Wir bilden die Divergenz der obigen Gleichung.

Da die Divergenz einer Rotation gleich Null ist, ergibt sich:

Mit div = erhalten wir schlielich die Kontinuittsgleichung: