5.4 Wechselstrom und Schaltkreise

[prev] [prev-tail] [tail] [up]

5.4 Wechselstrom und Schaltkreise

Allgemeine Beschreibung:

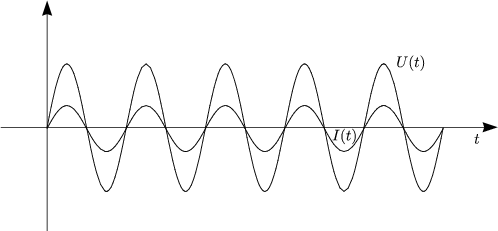
blicherweise beschreibt man die Spannungsverlufe durch Sinus- und Kosinusfunktionen.
$2p U(t) = U0 sin(wt+ f) mit w = T$
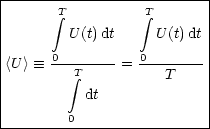
- Mittelwert: $|-------------------------| | integral T integral T | | U(t)dt U(t)dt| | | |<U > =_ -0-T---- = -0------ | | integral T | | dt | ---------0-----------------$
  
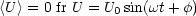
  $<U > = 0 fr U = U0sin(wt + f)$
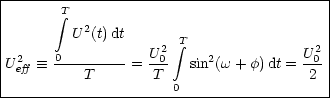
- Effektivwert: $|-----------------------------------------| | integral T | | U2(t)dt | | 2 integral T 2 | |Ue2ff =_ 0------- = U0- sin2(w + f)dt = U-0| | T T 0 2 | ------------------------------------------$
  
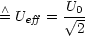
  $/\ U0- = Ueff = V~ 2$
  
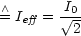
  $/\ = Ieff = I V~ 0- 2$
- Hausstrom: $Ueff = 230V,U0 = 325V$
Wechselspannung am OHMschen Widerstand:

Mit den KIRCHHOFFschen Gesetzen erhlt man:
$- U(t)+ U = 0 R$
Mit U₀ sint = U_R = I(t) ^. R erhlt man fr den zeitlichen Verlauf des Stroms:
$U |-------| I(t) =-0-sin wt =_ -I0sinwt-| R$

Leistung am Widerstand:
$2 P (t) = U (t).I(t) = U0 .I0 .sin (wt)$

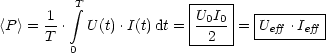
$integral T |-----| |-------| <P > =-1. U(t).I(t)dt =|U0I0 |= Ueff .Ieff| T 0 ---2--| ---------$
Wechselspannung am Kondensator:

$U = U (t) = U sinwt C 0$
Fr die Ladung des Kondensators gilt:
$|-------------------------| -Q(t) =-C-.UC-=-C-.U0-sinwt|$
Damit folgt fr den zeitlichen Verlauf des Stroms:
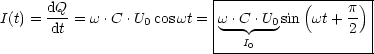
$dQ |-----------(----p-)| I(t) = ---= w .C .U0coswt =|w-.C .U0sin wt+ -- | dt | I0 2 | ---------------------$
Fr den kapazitiven Widerstand erhlt man:
$|---| R = U0-= |-1-| C I0 -wC--$
Dieser Ausdruck ist die sogenannte Impedanz.
- Keine absorbierte Leistung
- Phasenverschiebung
Kondensator und OHMscher Widerstand:

$-U (t)+ U + U = 0 R C$

$U(t) = I(t) .R+ Q(t)- C$

$dU- dI- I(t) dt = dt .R + c$
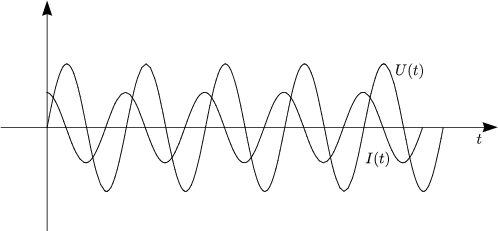
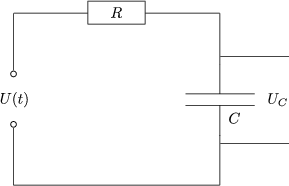
Dies ist eine Differentialgleichung, die wir mit folgendem Ansatz lsen:
$U (t) = U0sin wt$

$I(t) = I0sin(wt + f)$
Wir erhalten:
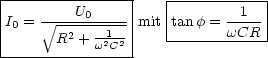
$|---------U0-----| |--------1---| |I0 = V~ -------- |mit|tan f = wCR--| | R2 + w21C2 | -------------| -----------------|$
Fr die Impedanz resultiert:
$|----- V~ ----------| |RL = R2 + -1---| -------------w2C2-|$
Fr R = 0 erhlt man den reinen kapazitiven Widerstand des Kondensators mit der Phasenverschiebung :
$|--------| | 1 | |---p-| |Rc = wC-|mit f = 2-| ---------- -------$
Wechselspannung an Spule:

$U (t) = L dI dt$

$dI- U0 sin wt = L dt$

$integral U |U------(----p-)| I(t) = -0-sinwtdt = |--0-sin wt- -- | L -w.L---------2---$
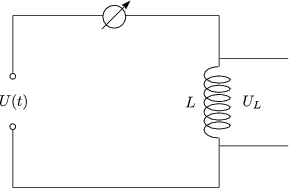
Fr den induktiven Widerstand gilt:
$|---------| |RL = w.L | -----------$
Spule und Widerstand: $|-----------------| |-----------| R = V~ R2-+-(wL)2-mit tan f = - wL --L--------------- ---------R---$
Serienschwingkreis:

$dU d2I dI I --- = L--2 + R. --+ -- dt dt dt C$

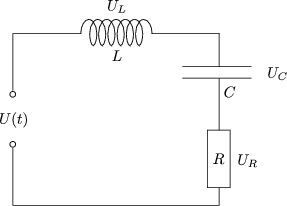
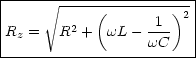
$|---- V~ -----------------| | ( 1 )2 | |Rz = R2 + wL - wC- | -------------------------$

$|---------------| | wL - -1-| |tan f = ---R-wC-| -----------------$

Resonanz:

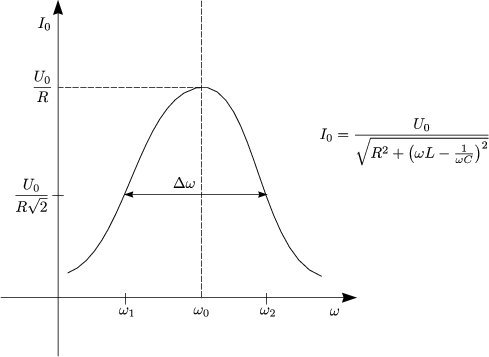
Das Maximum befindet sich bei ₀L = , das heit bei ₀ = . Also berechnet sich die Resonanzfrequenz nach:
$|-------1---| |w0 = V~ ----| -------L-.C--$
Man nennt diese Beziehung auch Thomsonsche Formel.
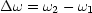
- Breite der Resonanzkurve $Dw = w2- w1$
  
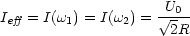
  $Ieff = I(w1) = I(w2) = V~ U0- 2R$
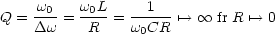
- Kreisgte $Q = -w0 = w0L-= --1-- '--> oo fr R '--> 0 Dw R w0CR$
Entladung eines Kondensators ber Spule und OHMschen Widerstand:

$Q- + R.I + LdI-= 0 C dt$

$I-+ R.I˙+ L.I¨= 0 C$
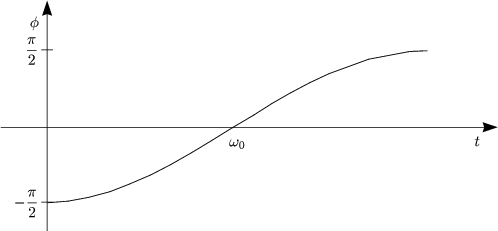
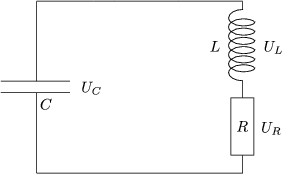
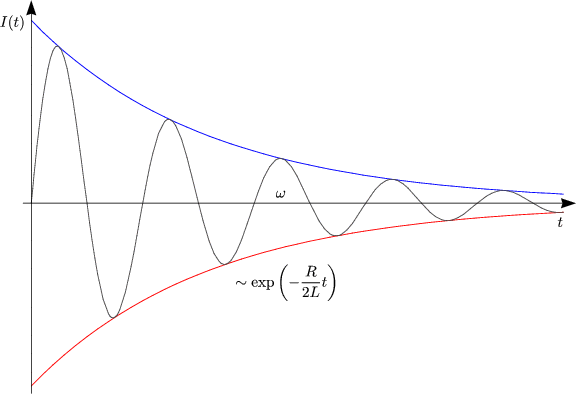
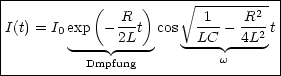
Wir verwenden als Ansatz eine exponentiell abfallende Kosinusfunktion:
$I(t) = I0exp (- at)coswt$
Damit erhalten wir als Lsung der Differentialgleichung:
$|----------(-----)---- V~ -----------| I(t) = I exp --R-t cos -1- - R2-t | | 0 2L -LC- --4L2 | | -Dmpfung- w | ------------------------------------$
Graphisch sieht diese Funktion folgendermaen aus:

[prev] [prev-tail] [front] [up]