Im Vakuum gilt natrlich ![]() = 0 und
= 0 und ![]() =
= ![]() . Wir betrachten als Ausgangspunkt das
System der MAXWELL-Gleichungen:
. Wir betrachten als Ausgangspunkt das
System der MAXWELL-Gleichungen:
Wir bilden nun jeweils die Rotation der dritten Gleichung:
Nun folgt durch Auflsen des doppelten Kreuzproduktes und mit der ersten und vierten MAXWELL-Gleichung:
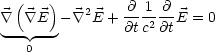
Somit gilt:
Damit ergibt sich also die Wellengleichung fr das elektrische Feld ![]() :
:
Die Lichtgeschwindigkeit im Vakuum berechnet sich folgendermaen:
In Medien folgt mit der entsprechenden Dielektrizittszahl ![]() r und der Permeabilittszahl
r und der Permeabilittszahl
![]() r:
r:
Im Vakuum gilt also v = c. Die Wellengleichung des magnetischen Feldes ![]() folgt
analog:
folgt
analog:
Die zugehrige Dispersionsrelation lautet:
Damit folgt also:
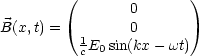
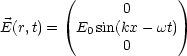
Die Vektoren des elektrischen und magnetischen Feldes stehen somit senkrecht aufeinander:
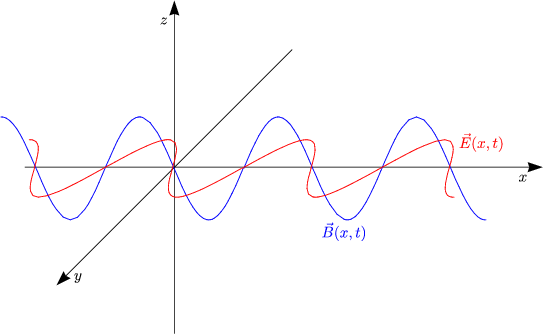
Der Vektor senkrecht auf ![]() und
und ![]() zeigt somit in Richtung des Ausbreitungsvektors
zeigt somit in Richtung des Ausbreitungsvektors
![]() der elektromagnetischen Welle. Speziell gilt fr unser Beispiel:
der elektromagnetischen Welle. Speziell gilt fr unser Beispiel:
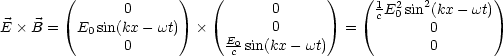
Man kann zeigen, da die beiden Energiedichten gleich gro sind:
Mit der zuvor berechneten Energiedichte w erhalten wir:
Fr die zeitlich gemittelte Intensitt folgt:
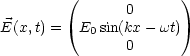
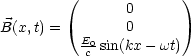
Fr die Energiedichte erhalten wir:
Wir wollen diese Gre zeitlich mitteln. Dazu mitteln wir die quadratische Sinusfunktion ber volle Perioden hinweg, womit folgt:
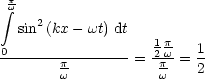
Der Mittelungsfaktor ist also gleich ![]() . Damit gilt also:
. Damit gilt also:
Fr die zeitlich gemittelte Intensitt folgt:
Auerdem definieren wir den sogenannten Poynting-Vektor (Intensittsvektor):
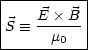
Speziell fr unser Beispiel gilt:
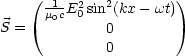
Der Poynting-Vektor zeigt also die Richtung des Energieflusses an, whrend der Betrag dessen Gre angibt.
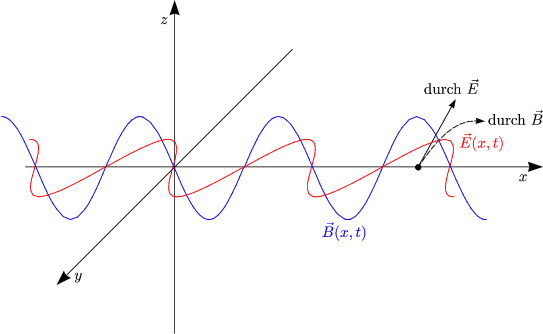
Fr die Kraft des elektrischen Feldes auf die Ladung q ergibt sich:
Damit folgt fr die Geschwindigkeit der Ladung:
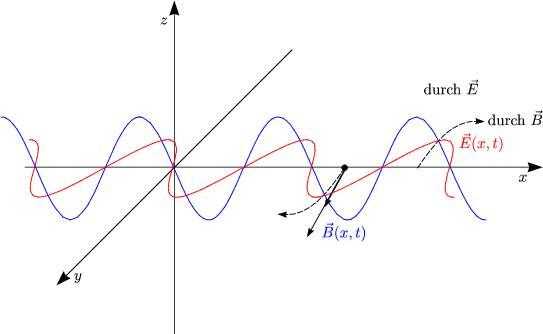
Darber hinaus resultiert fr die Kraft des magnetischen Feldes auf die Ladung q:
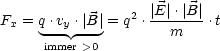
Mit dem zweiten NEWTONschen Axiom ![]() =
= ![]() folgt natrlich durch Integration:
folgt natrlich durch Integration:
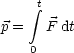
Hier gilt nun:
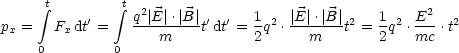
Vergleiche mit Energie der Ladung:
Dabei handelt es sich also um den Zusammenhang zwischen Impuls und Energie des elektromagnetischen Feldes. Infolge des Impulses der elektromagnetischen Welle ergibt sich folgender Strahlungsdruck PS:
Damit ergibt sich folgender Strahlungsdruck:
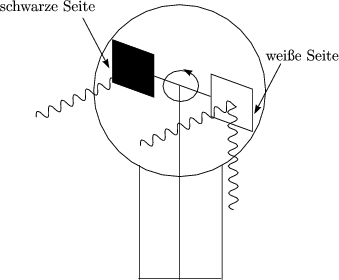
Die Lichtmhle dreht sich allerdings nur dann in die eingezeichnete Richtung, wenn im Gef ein perfektes Vakuum herrscht.
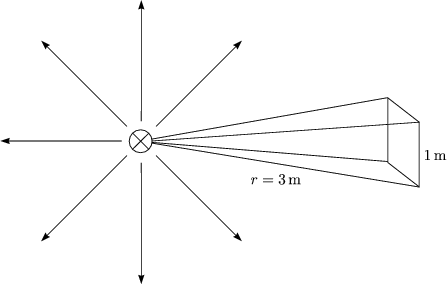
Die Intensitt ist umgekehrt proportional zum Quadrat des Abstandes r. Fr r = 3m resultiert:
Mit der Strahlungsleistung Ptot = 50W erhalten wir:
Vergleiche mit Atmosphrendruck:
Auerdem berechnet sich das Magnetfeld in r = 3m Entfernung:
Damit gilt fr das elektrische Feld in r = 3m Entfernung:
Dieses Prinzip findet Anwendung beim Antrieb von Raumschiffen mit Solarsegeln.