
Untersuchungen mit Drehwaage: ___________________________

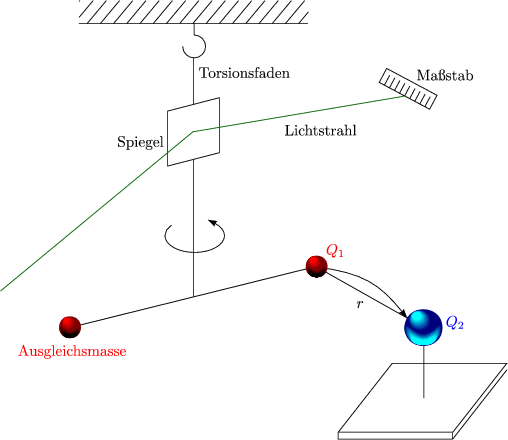
Elektromagnetische Kraft zwischen Q1,Q2 im Gleichgewicht mit Rckstellkraft des Torsionsfadens.


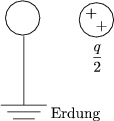

Dann ergibt sich schlielich fr die Kraft F12' zwischen den neuen Ladungen:
Daraus ergibt sich dann folgende Proportionalitt:
![]()
Nach dem 3.NEWTONschen Axiom ist die Kraft genauso gro wie deren Gegenkraft:
Wenn Q1 positiv ist, dann ist Q2 negativ.
![]()
Die Natur ist elektrisch neutral.
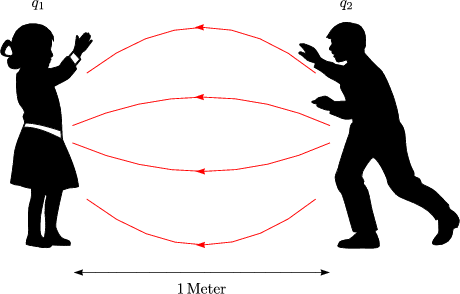
Gravitationskraft:
Wenn alle Mnner 1% mehr Elektronen als Protonen, alle Frauen 1% mehr Protonen als Elektronen htten ...



(Superpositionsprinzip)
Diese Ladungsverteilung beinhaltet praktisch unendlich viele Ladungen, deren einzelnen Werte gegen 0 gehen:

Wir fhren die Ladungsdichte ![]() ein.
ein.
Demnach berechnet sich die Kraft durch den folgenden Grenzbergang:

Die Summe geht also hierbei in ein Volumenintegral ber. Fr die Gesamtladung selbst folgt durch Integration ber die Ladungsdichte:
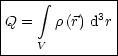
Hier arbeiten wir mit der sogenannten Flchenladungsdichte, welche folgendermaen definiert ist:
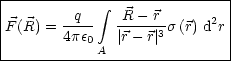

Die Gesamtladung berechnet sich durch Integration ber die Flche:


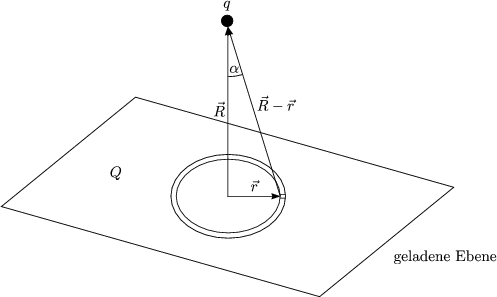
Die horizontale Komponente von d![]() mittelt sich aufgrund der Rotationssymmetrie
weg, es verbleibt nur die vertikale Komponente dF
mittelt sich aufgrund der Rotationssymmetrie
weg, es verbleibt nur die vertikale Komponente dF![]() .
.
Mit r = R . tan![]() folgt:
folgt:

Sie ist somit unabhngig vom Abstand R.

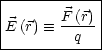
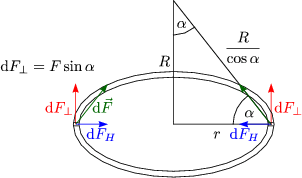
Die elektrische Feldstrke ist also definiert als Kraft einer Ladungsverteilung auf q, dividiert durch q.


Mit ![]() = q .
= q .![]() folgt hier:
folgt hier:

Die Beschleunigung sei konstant.
Nach Durchlaufen der Strecke L hat das Elektron somit die Geschwindigkeit:

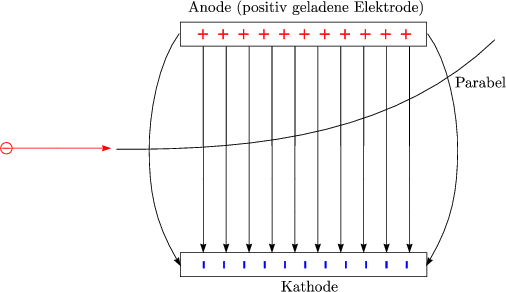
Fr die Beschleunigung ergibt sich hier vektoriell, da die beschleunigende Kraft nur in Richtung der y-Achse wirkt:
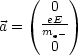
Die Geschwindigkeit v(t) und der zurckgelegte Weg s(t) folgt durch Integration:

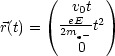
Daraus resultiert die Bahnkurve:
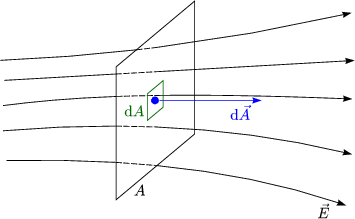
Der Flu ![]() durch das Flchenelement d
durch das Flchenelement d![]() (Flchennormale fr dA) ist folgendermaen
definiert:
(Flchennormale fr dA) ist folgendermaen
definiert:
Wir unterscheiden dabei folgende Flle:
Somit folgt fr ![]() :
:
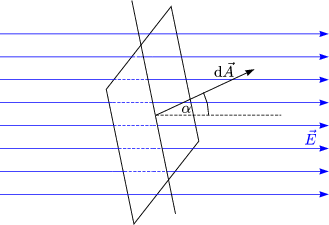
Fr ![]() = 90o ergibt sich
= 90o ergibt sich ![]() = 0.
= 0.


Hier sei folgender Hinweis gegeben:
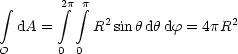
| |
| Flu aus beliebiger geschlossener Flche ist proportional zur umschlossenen Ladung Q, unabhngig von der Ladungsverteilung. |
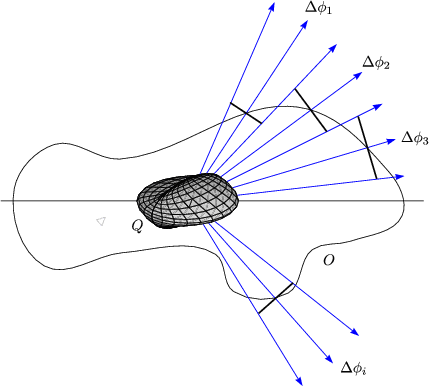
Der Flu durch eine Teilflche ist bei konstantem ffnungswinkel unabhngig vom
Abstand, daher gilt ![]()
![]() 1 =
1 = ![]()
![]() 2 = ... =
2 = ... = ![]()
![]() i.
i.
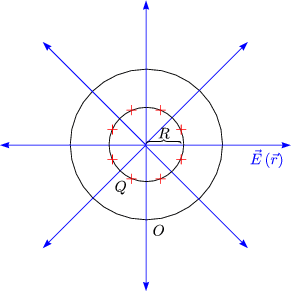
Definiere geschlossene Oberflche (GAUsche Flche)
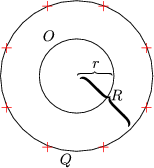
Das elektrische Feld ist im Innern somit gleich 0:
Elektrische Felder verschwinden innerhalb von leitenden Materialien.
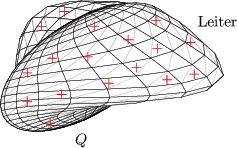
Die Ladungen sind beweglich und stoen sich somit ab.
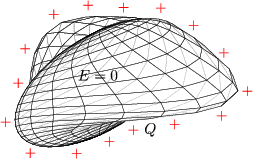
Dies ist der bekannte Faraday-Effekt.
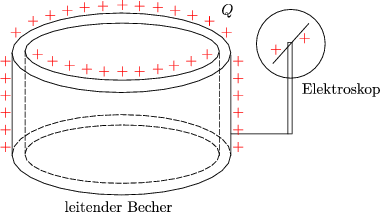
Wird Ladung im elektrischen Feld verschoben, wird Arbeit geleistet, die zur nderung der potentiellen bzw. kinetischen Energie fhrt.
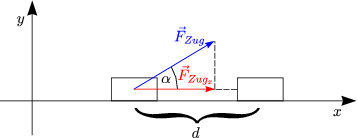
Die Arbeit ist allgemein definiert als Produkt aus Kraft und Weg:
Wenn ![]() = 90o ist die geleistete Arbeit W gleich 0. Arbeit wird durch
eine Kraft geleistet, die auf ein Teilchen in Bewegung ausgebt wird. Wir
veranschaulichen diesen Sachverhalt mit einem Beispiel aus der Mechanik:
= 90o ist die geleistete Arbeit W gleich 0. Arbeit wird durch
eine Kraft geleistet, die auf ein Teilchen in Bewegung ausgebt wird. Wir
veranschaulichen diesen Sachverhalt mit einem Beispiel aus der Mechanik:

Falls |F| = m.g ist W = mg(y2-y1) die Arbeit, welche durch F geleistet wird. Die Arbeit durch die Erdanziehungskraft ist beispielsweise gegeben durch:
Fhrt eine Kraft ![]() zu einer Beschleunigung (oder auch Abbremsung), so
ndert sich die kinetische Energie (Bewegungsenergie) des Teilchens, auf
das die Kraft ausgebt wird.
zu einer Beschleunigung (oder auch Abbremsung), so
ndert sich die kinetische Energie (Bewegungsenergie) des Teilchens, auf
das die Kraft ausgebt wird.

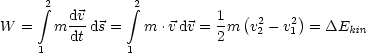
Wirkt arbeitende Kraft in einem Feld, so ndert sich die potentielle Energie
des Teilchens.

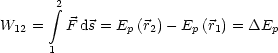
Im geschlossenen System (keine externen (resultierenden) Krfte) gilt:
Die ist die einfachste Form des Energieerhaltungssatzes.
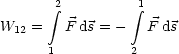
Die geleistete Arbeit ist wegunabhngig, wenn das Integral ber einen geschlossenen Weg (Ringintegral) verschwindet:
Ein Kraftfeld ist dann konservativ, wenn es eine Funktion V gibt, so da sich die Kraft als Gradient dieser Funktion V schreiben lt:
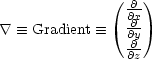
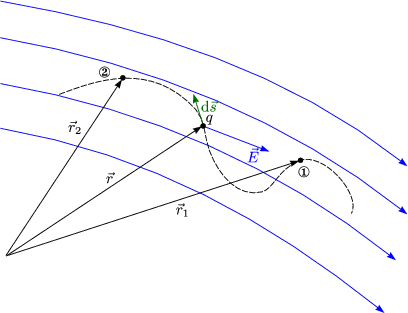
Das elektrostatische Feld bt eine Kraft auf eine Ladung q aus und leistet Arbeit, wenn q sich bewegt.

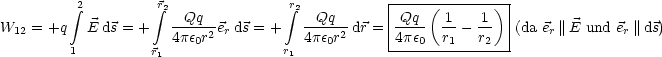

Insbesondere gilt:
Entlang dieses Weges gilt r = const. d![]() steht somit senkrecht auf dem
Vektor des elektrischen Feldes
steht somit senkrecht auf dem
Vektor des elektrischen Feldes ![]()
![]() . Damit ist also die geleistete Arbeit
W23 gleich 0:
. Damit ist also die geleistete Arbeit
W23 gleich 0:
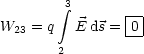
Hier ist also d![]() parallel zum
parallel zum ![]() -Vektor. Die geleistete Arbeit ist hier im
Gegensatz zum ersten Fall nicht 0, sondern betrgt:
-Vektor. Die geleistete Arbeit ist hier im
Gegensatz zum ersten Fall nicht 0, sondern betrgt:
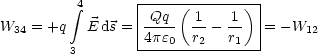
Auch allgemein gilt:
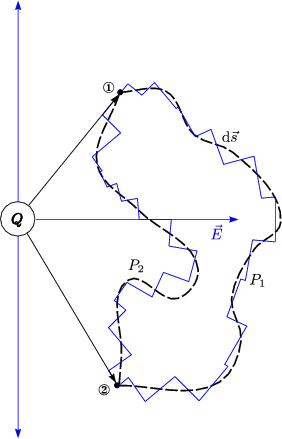
P wird in Elemente senkrecht und parallel zum Vektor des elektrischen Feldes aufgeteilt.
![]()
Fr das Goldatom gilt Z = 79, es besitzt also 79 Protonen. Des weiteren betrgt der Radius R etwa 6,6 . 10-15 m. Damit folgt also:
Dies ist die Einheit fr das Potential.

Eine weitere wichtige Gre ist die Spannung U = ![]() V . Insbesondere gilt:
V . Insbesondere gilt:
1eV ist die Differenz an kinetischer Energie einer Elementarladung nach Durchlaufen
einer Spannung von 1 V.
Flchen mit V =const. ![]()
![]()

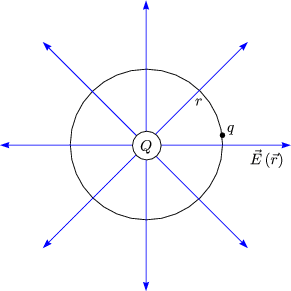
| Wird eine Probeladung q lngs einer quipotentialflche bewegt, findet hier keine Energienderung statt. |


Physikalisch relevant ist die Potentialdifferenz. Im geschlossenen System gilt:
Da eine Integralgleichung schwerer zu lsen ist, notieren wir uns die differentielle Form:

Fr x1![]() x2 folgt nun:
x2 folgt nun:
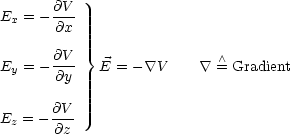
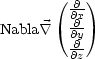
Fr Skalare ist dies der Gradient, fr Vektoren die sogenannte Divergenz.

Jetzt unterteilen wir das Volumen in infinitesimal kleine Wrfelchen:
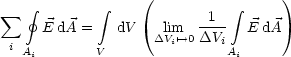

Wir berechnen den Flu durch die sechs Flchen des Wrfels. Fr den Flu durch die Flche A1 gilt nach der allgemeinen Formel:
Die Flche A2 befindet sich in einer Entfernung von ![]() x von der Flche A1. Die
x-Komponente des elektrischen Feldes hat somit den Wert Ex(x +
x von der Flche A1. Die
x-Komponente des elektrischen Feldes hat somit den Wert Ex(x + ![]() x), womit
sich fr den Flu
x), womit
sich fr den Flu ![]() 2 ergibt:
2 ergibt:
Mit Hilfe der Taylor-Formel knnen wir fr kleine ![]() x die Funktion E(x +
x die Funktion E(x + ![]() x)
entwickeln:
x)
entwickeln:
Damit folgt nun endgltig fr ![]() 2:
2:
Analog gilt fr den Flu durch die restlichen Flchen A3 bis A6:
Somit gilt fr den gesamten Flu:
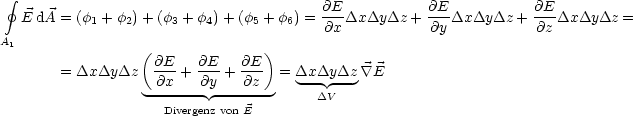 | (2.1) |
Durch Koeffizientenvergleich ergibt sich:
Dies ist die 1.MAXWELLsche Gleichung in differentieller Form.
Wir haben hier die sogenannte Poisson-Gleichung hergeleitet.
Damit folgt:

Wie nah kommt Teilchen an Q, das bei r = ![]() mit v
mit v![]() losluft? Dazu
betrachten wir die Energiebilanz:
losluft? Dazu
betrachten wir die Energiebilanz:
Damit folgt rmin zu:

Fr Etot < 0 liegt ein gebundener Zustand vor. Das Teilchen kann maximal bis rmax kommen:
Damit folgt dann rmax:
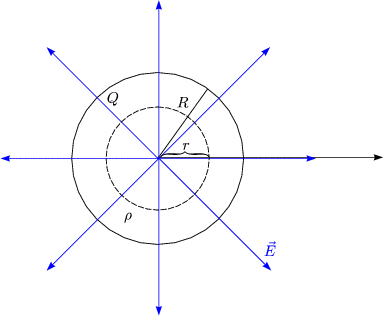
Damit lt sich dann die Ladung angeben:

Zur Berechnung der elektrischen Feldstrke nehmen wir den GAUschen Satz:
Die elektrische Feldstrke ist betragsmig auf der Kugeloberflche konstant, so da wir sie vor das Integral ziehen knnen:
Damit ergibt sich dann E(r):
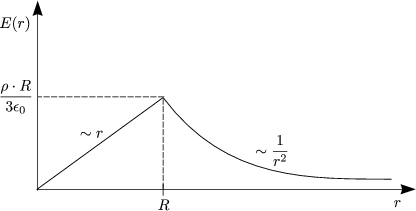
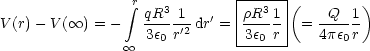
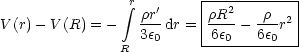
Damit sieht die Funktion V (r) folgendermaen aus:


Fr l » r knnen die Randflchen des Drahtes vernachlssigt werden. Damit folgt fr seine Flche:
Die Lngenladungsdichte sei entlang des Drahtes konstant:
Auf der Oberflche des Drahtes ist nun E wieder betragsmig konstant. Wir knnen so wie bei der Kugel verfahren und E vor das Integral ziehen:
Damit resultiert also schlielich fr E:
Das elektrische Feld eines sehr langen Drahtes verhlt sich also fr r![]()
![]() anders als das Feld einer auf einen kleineren Raumbereich konzentrierten
Ladungsverteilung. Deren Feldstrke fllt fr r
anders als das Feld einer auf einen kleineren Raumbereich konzentrierten
Ladungsverteilung. Deren Feldstrke fllt fr r![]()
![]() proportional zu
proportional zu ![]() ab; sie
verhlt sich also wie eine Punktladung:
ab; sie
verhlt sich also wie eine Punktladung:
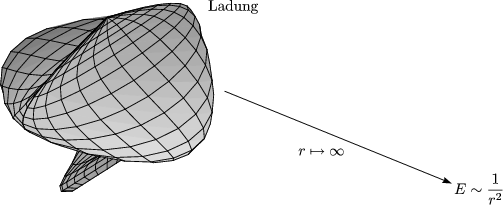
Fr das Potential des Feldes eines sehr langen Drahtes folgt durch Integration:

Betrachten wir eine Ansammlung ungleichnamiger Ladungen:
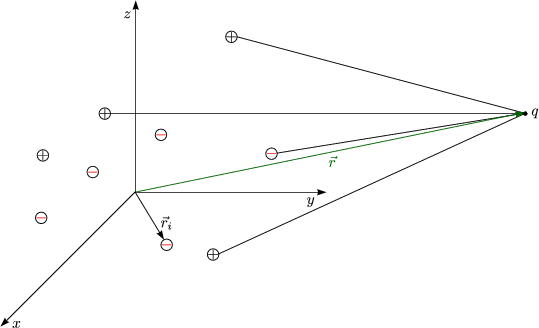
Es gilt wie immer das Superpositionsprinzip:

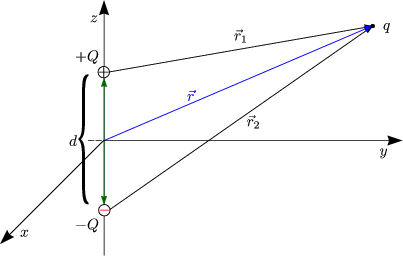
Die beiden Ladungen, aus denen der Dipol besteht, sind betragsmig gleich gro; sie haben nur entgegengesetzte Vorzeichen:
Damit ergibt sich dann fr das Potential:
Durch Umformung erhalten wir:

Wir nhern diese Beziehung durch eine Taylorreihenentwicklung:

Somit erhlt man das Potential eines Dipols:
![( )
(( ) ( )) ( dr ( ) )
E (r) = - \~/ V (r) =--Q dr \~/ -1 + 1- \~/ dr = ---Q- - 3-----.r + 1- d . \~/ r =
4pe0 r3 r3 4pe0 r4 r r3
[ ] |_ ( )( )_ |
-Q-- dr -1 ( ) --Q- |_ dr 1- -@- @-- @-- x _|
= - 4pe0 - 3r4er + r3 d. \~/ r = -4pe0 -3 r4er + r3 . d1@x + d2@y + d3@z y =
[ ] [ ] z
-Q-- dr -1 -1-- Qd-.r -1 --1-[ p.r.cosh- 1- ]
= - 4pe0 - 3r4er + r3 .d = 4pe0 3 r4 er- r3 .Qd = 4pe0 3 r4 er- r3 .p =
|-------------------|
= |--1---(3pcoshe - p)|
-4pe0r3--------r-----](ex271x.gif) | (2.2) |
Mit der Taylorentwicklung folgt:
![( ( ) ( )) ( [ ] [ ] )
F = Q . E r+ d - E r- d ~~ Q . E(r)+ d \~/ E - E(r) - -d \~/ E =
2 2 2 2
( ) ( )
= Q . d \~/ E = p \~/ .E /= o](ex287x.gif) | (2.3) |
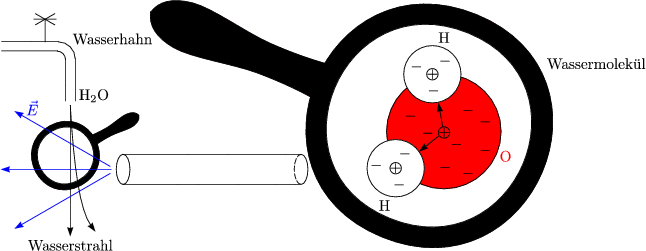
Wassermolekle haben ein Dipolmoment, da die Elektronenwolke asymmetrisch ist.
Daraufhin richten sich diese im elektrischen Feld des Stabes aus, womit der Wasserstrahl abgelenkt wird.