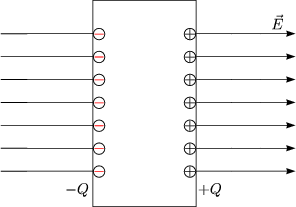

Ein Kondensator besteht aus zwei entgegengesetzt geladenen leitenden Flchen.
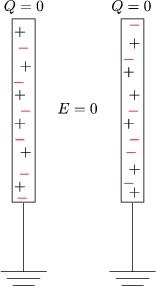
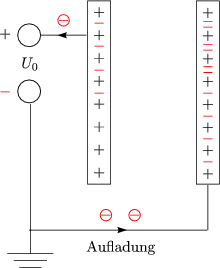

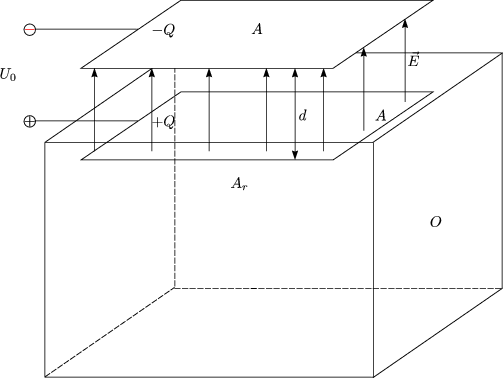
Wir legen eine geschlossene Flche O um Q herum. Diese geschlossene Flche wird durch einen Quader realisiert:
Ar ist hierbei die Restflche, also O - A. Fr den Flu folgt somit:
Damit ergibt sich fr das elektrische Feld:
Die Spannung (Potentialdifferenz) folgt nun durch Integration ber das elektrische Feld entlang eines Weges von der einen zur anderen Platte.
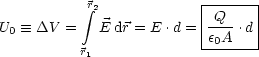
Damit ergibt sich schlielich die Kapazitt nach der Definition Q = C .U0:
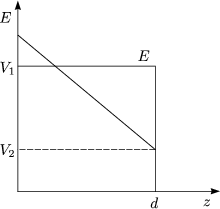
Dann folgt eine Kapazitt von 88,5pF.
Die Kapazitt ist eine Eigenschaft des Leiters, dessen Geometrie und dem Isolator zwischen den Flchen.
Folgende Kapazitten sind blich:
Kondensatoren sind nichts anderes als Ladungsspeicher.
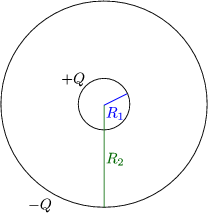
Fr R1![]()
![]() folgt:
folgt:
Damit ergibt sich die Kapazitt einer frei stehenden Kugel:

Mit Q = Q1 + Q2 ergibt sich:
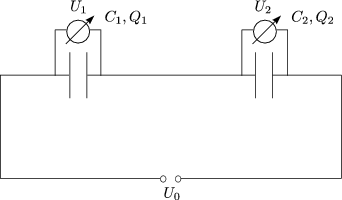
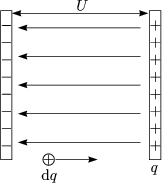
Bei der Verschiebung der positiven Ladung dq mu Arbeit aufgewendet werden:
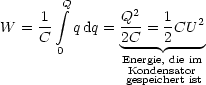
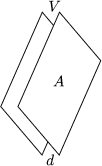
Damit folgt fr die Energiedichte:
Die gespeicherten Energien in Kondensatoren sind sehr gering. Batterien beispielsweise besitzen Energien von 104 Ws und mehr.
(Isolator im elektrischen Feld)
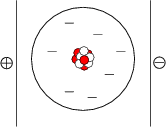
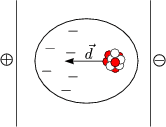
Ein Atom im elektrischen Feld bildet Dipolmoment aus. (d ![]()
![]() rAtom)
rAtom)
Der Proportionalittsfaktor heit Polarisierbarkeit und ist materialabhngig.
| H | He | Li | C | Ne | |
| | 0,66 | 0,21 | 12 | 1,5 | 0,4 |
Auerdem folgt weiter, indem wir die neue Gre ![]() einfhren:
einfhren:
![]() ist die dielektrische Suszeptibilitt.
ist die dielektrische Suszeptibilitt.
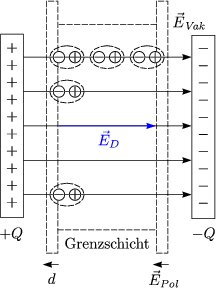
Fr die Flchenladungsdichte ergibt sich:
Fr den Flu im Vakuum folgt:
Damit resultiert das elektrische Feld im Vakuum:
Analog ergibt sich fr Ep:
Das resultierende Feld im Dielektrikum kann nun berechnet werden durch:
Damit folgt dann schlielich:

Im Vakuum gibt es virtuelle Teilchen-Antiteilchenpaare, die sich im E-Feld ausrichten. Damit wird also das E-Feld kleiner! Die Konsequenz ist, da das atomare Feld geringfgig vom COULOMBfeld abweicht.
Das Feld im Dielektrikum ist kleiner als im Vakuum:
Hier sind einige Werte fr die Dielektrizittszahl aufgelistet:

Die Kapazitt ist im Dielektrikum grer:
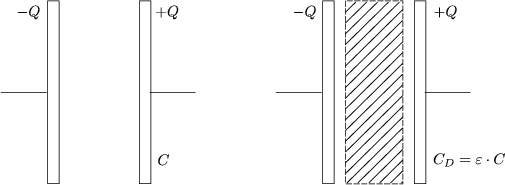
Mit U = E . d folgt fr die Spannung im Dielektrikum:
Damit gilt also folgende Beziehung zwischen der Kapazitt eines Plattenkondensators mit Dielektrikum und ohne:
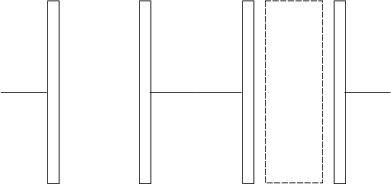
Schaltet man einen Kondensator mit und einen ohne Dielektrikum in Reihe, so gilt: