4.1 Magnetfeld stationrer Strme

4.1.1 Punktladung im Magnetfeld

Die Punktladung erfhrt die sogenannte Lorentzkraft:

|-----------| |F = q.v× B | -------------

Das Teilchen durchluft eine Kreisbahn:

v2 q.v.B = m .a = m .-r

Damit folgt der Radius r der Kreisbahn:

|---------| |r = m-.v-| -----q.B--|

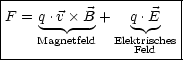
LORENTZkraft: $|---------------------| F = q.v× B + q.E | | -- -- | | | ----Magnetfeld--ElekFtreisldches-$
Im E-Feld erfhrt q eine lineare (zeitlich konstante) Beschleunigung:
$F = q.E = m .a$
Wir lsen nach auf:
$|-------| | qE | |a = m--| --------$
Im B-Feld erfhrt q eine Zentripetalbeschleunigung:
$F = q .v× B = m .a$

$|---------------| | q-.v.B- v2| -a =---m---=--r--$

$|----m-.v-| |r = -----| -----q.B--|$

Demonstration: WEHNELT-Rohr (Fadenstrahlrohr)

$E = e.U = 1mv2 2$
Nach der Beschleunigung hat das Teilchen eine Geschwindigkeit v von:
$V~ ---- 2eU- v = m {300V}$
Im -Feld durchluft es dann eine Kreisbahn mit dem Radius:
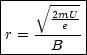
$|---------| | V~ 2mU| r = ---e--| ------B----$
Damit kann experimentell die spezifische Ladung bestimmt werden:
$|---------| |e-= -22U-2| -m---r-B---$
Fr Elektronen liegt diese in folgender Grenordnung:
$e-= 1,8.1011-C m kg$
- Umlauffrequenz:
  Mit T = = = ergibt sich:
  $n = 1-= q-.B- T 2pm$
  
  $2p q.B w = --= ---- ----T ---m- Zyklotronfrequenz$
  
  Beispiel:
  Mit B = 12G erhlt man fr die Zyklotronfrequenz: $Vs As |----------| w = 12 -2-.10-4 .1,8.104--= -2,2.108Hz-|(!) m kg$
  Das heit:
  $|-----7 m-| v ~~ 10 s (!) ----------$
Anwendungen:
- Massenspektrometer:
  
  $Quelle: m, q$
  
  $m = B2-.r2 .q 2U$
  
  $U = UG2- UG1$
- Magnetische Flaschen/Fallen
- Teilchenbeschleuniger
  - Zyklotron:
    
    Die Umlauffrequenz ist konstant:
    $-e-- n = 2pm .B = const.$
    Der Energiegewinn pro Umlauf betrgt 2 ^.<U>^. e.
    Beschleunigung und Bewegung kommt aus der Phase.
    Das Zyklotron funktioniert nur fr v « c beispielsweise fr Protonen E ~ 10MeV
  - Synchrotron
    Dieses benutzt man fr relativistische Teilchen (v c).
    $m = const.$
    
    Dies funktioniert so, da B mit der Energie von q ansteigt.
- Detektoren:
  
  Man benutzt Detektoren zur Impulsbestimmung von geladenen Teilchen (auch Ladung).
  $p = q.B .r$
  
  $GeV- [p] = 1 c$
  
  $[q] = 1e$
  
  $[B] = 1 T$
  
  $[r] = 1m$
  
  $==> p = 0,3.q.B .r$
  
  4.1.2 Krfte auf Strme im Magnetfeld
  
  Fr die Kraft auf ein einzelnes Elektron, das sich mit der Driftgeschwindigkeit _D im Magnetfeld bewegt, ergibt sich:
  $Fi = q.vD × B$
  Gesamtstrom durch Integration ber die Querschnittsflche A des Leiters:
  $integral integral I = jdA = r .vDdA = r .vD .A A A$
  Fr die Ladungstrgerdichte gilt:
  $r = Q-= -Q-- V l.A$
  Gesamtladung in einem Leiter der Lnge l:
  $|-------| | I .l Q = v--| ------D--$
  Daraus ergibt sich die Kraft auf einen stromdurchflossenen Leiter:
  $F = Q .vD× B = I .l.vD-× B vD$
  
  $|-----------| | | -F-=-I .l×-B-$
  Differentiell gilt:
  $dF = I dl× B$
  Als verallgemeinerten Ausdruck fr erhlt man schluendlich:
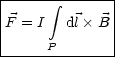
  $|----- integral ------| |F = I dl× B | | P | ---------------$
  
  Demonstration: Leiterschleife im Hufeisenmagneten

Homogene Leiter: $F = I .l× B$
Allgemeine Leiter: $integral F = I dl× B P$

Sonderfall:

Kraft auf Leiterschleife:

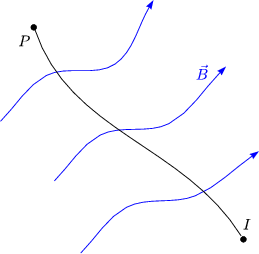
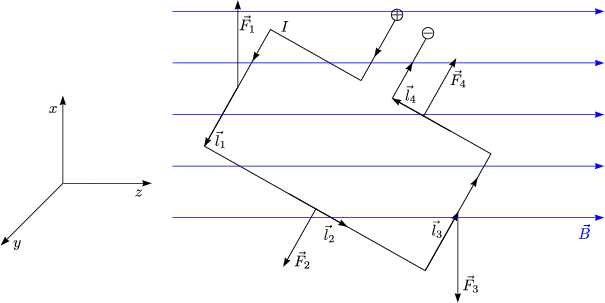
Die Krfte ₁ und ₃ sind betragsmig gleich gro, aber entgegengesetzt gerichtet:
$( ) F3 = -F1 l3 = -l1$
Dies ist auch bei ₂ und ₄ der Fall:
$F4 = -F2$
Die Summe aller Krfte ist somit gleich Null:
$sum Fi = o i$

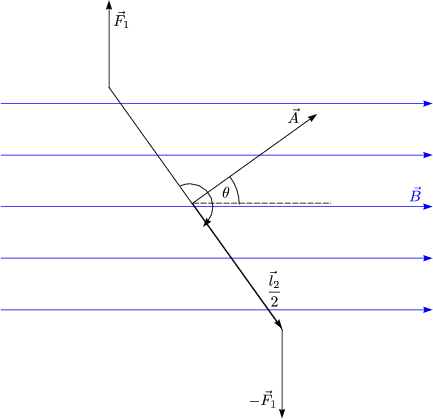
Die Krfte verursachen aber ein Drehmoment:
$M = -l2 ×F1 + l2× (-F1) 2 2$

$|------------| M = -l2× F1 | --------------$
Das Drehmoment zeigt in die Papierebene hinein. Die Kraft berechnet sich nach der zuvor hergeleiteten Beziehung:
$F1 = I .l1× B$
Damit folgt dann fr den Betrag des Drehmoments:
$|------------| |M |= I .l1 .l2 .B .sinh =-I .A-.B-.sinh|$
Mit dem magnetischen Dipolmoment = I ^. ergibt sich schlielich:
$|---------------------| |M = I .A × B = m × B| ----------------------$
Zusammenfassend kann man sagen: Krper mit magnetischem Moment erfahren ein Drehmoment im B-Feld.
Spule im B-Feld:

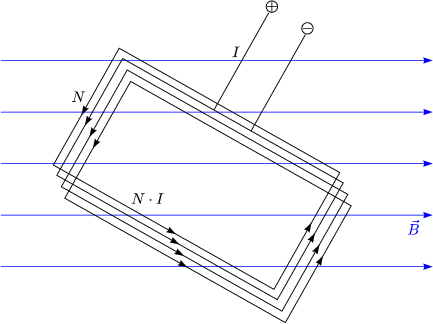
Da eine Spule aus N solchen Leiterschleifen besteht, folgt fr das magnetische Dipolmoment:
$m = N .I .A$
Anwendungen:
- Galvanometer zur Strommessung
- Elektromotor:
Funktion:

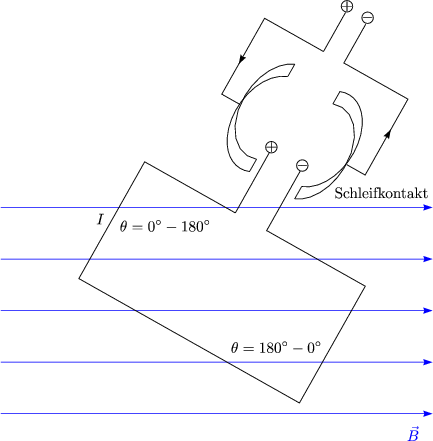
Der Strom wechselt die Richtung bei der Drehung. Drehmoment immer in eine Richtung
4.1.3 Der HALL-Effekt

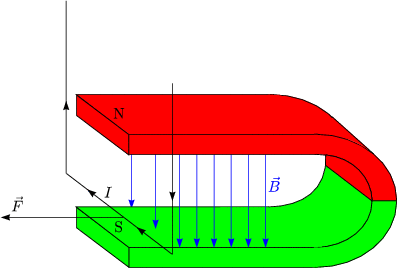
Trennung von Ladungen im stromdurchflossenen Material im -Feld

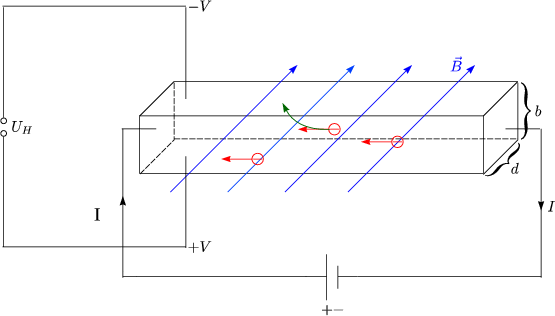
Die Elektronen driften nach oben, bis ein Gleichgewicht entsteht:
$F = q.v .B = q .E = F m D e$
Es baut sich die sogenannte Hallspannung auf:
$|-------| UH = b .E = vD-.B-.b-$

Messungen:
- Magnetfelder: $UH B = vD-.b$
  
  Beispiel:
  Es bestehe ein Magnetfeld B = 1T, die Dicke b der HALLsonde sei 1cm. Auerdem gilt fr die Driftgeschwindigkeit v_D der Elektronen: $vD = 10-5 m- s$
  Damit ergibt sich also folgende HALLspannung:
  $-5 m -2 |------| UH = vD .B .b = 10 s-.1T .1.10 m = -100nV-|$
- Ladungstrgerdichte:
  Die Stromstrke I lt sich in folgende Terme zerlegen:
  $|---------------| |I = n|.q .vD-.A-| | VLoadluumngenVoluZemiten | -----------------$
  Wir lsen nach der Ladungstrgerdichte n auf:
  $I I n = A-.v--.e = b.d.v--.e- D D$
  Mit der HALLspannung U_H lt sich n berechnen:
  $|-----I .B--| n = --------| ----e-.d.UH--$
- Materialeigenschaften:
  - U_H = A_H ^. $A /\ = HALL -Konstante H$
  - R_H = A_H ^. $/\ RH = HALL -Widerstand$
  Sonderfall: Quanten-HALL-Effekt (V.KLITZING (1980, 1985))
  
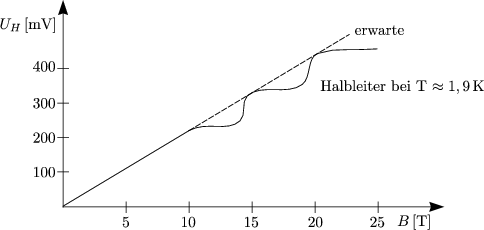
  Die Spannung wchst in Quantensprngen. Der Widerstand ist also gequantelt.
  $-34 RK =_ -h = -6,63-.10---Js ~~ 25813_O_ ----e2 (1,6.10-19C)2 Widerstands- V.KLITZING- normal Konstante$
  
  $RK RH = N-- mit N = 1, 2, 3, ...$

4.1.4 Magnetfelder von bewegten Ladungen

|-----------| | 1- | |B = c2v× E | -------------

Fr eine bewegte Ladung gilt:

B = 1-v× --1- q-er = --1---q.v-×-r c2 4pe0 r2 4pe0c2 r3

Mit ₀ = = 4 ^. 10^-7 = 4 ^. 10^-7 folgt:

|----m---q.v-×r-| |B = -0-.---3---| -----4p----r-----

Man erkennt die Analogie zum COULOMBgesetz.

,
|| q, v,

4.1.5 Magnetfeld von Strmen

/\ q .v = I .dl

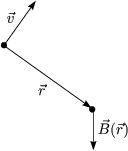
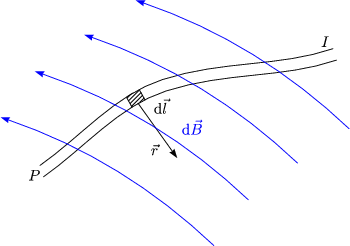
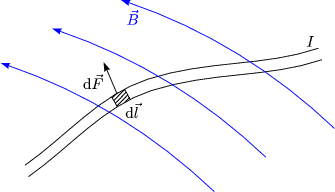
Fr das Feld eines Stromelements I ^. d gilt somit:

m0- I .dl×-r dB = 4p . r3

Durch Integration erhalten wir das BIOT-SAVARTsche Gesetz:

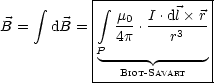
|--------------| integral | integral m0 I-.dl×-r| B = dB = | 4p . r3 | |P------ ------| ----BIOT-SAVART----

Beispiel:

Magnetfeld einer Leiterschleife im Mittelpunkt:

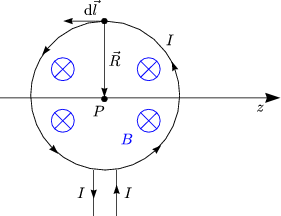
Differentiell gilt:
$m0- -R- dB = 4p .Idl× R3$
zeigt in Papierebene hinein. Da d gilt:
$gf gf |-------| B = m0.I .1--.dl.sin(90o).e = m0--I- dl.e = m I-e | P 4p R2 z 4p R2 -- z --02R-z-| 2pR$
Magnetfeld einer Leiterschleife auf der Achse durch Mittelpunkt:

Hier gilt d d + .
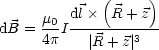
$( ) m0 dl× R + z dB = 4p-I--------3--- |R +z|$
Fr das Feld in z-Richtung folgt:
$sinh = V~ -R----- R2 + z2$

$|-------------| m0 dl R |m0 I dlR | dBz = dB sin h = 4p-I|R-+z|2 . V~ R2-+-z2 =|4p-(z2 +-R2)32 --------------$
Durch Integration gilt dann wieder:
$gf gf m0- ----R----- Bz = dBz = 4p .I .(z2 + R2)32 dl 2pR$

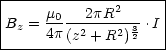
$|-------------------| B = m0--2pR2----.I| | z 4p (z2 + R2)32 | ---------------------$
Aufgrund der Zylindersymmetrie gilt B_x = 0 und B_y = 0. Fr groe Abstnde (z » R) ergibt sich:
$Bz = m02pR2-I 4p z3$
Mit dem magnetischen Moment m R²I resultiert das magnetische Dipolfeld:
$|-----------| | m0 2m | |Bz = 4p-z3-| ------------$
Vergleiche mit elektrischem Dipolfeld:
$|-----------| |E = -1--2p ,p= /\ Elektrisches Dipolmoment -----4pe0z3--$
Zylinderspule:
Die Spule habe den Radius R, die Lnge l und bestehe aus N Windungen. Fr die Dichte der Windungen gilt:
$N n = -l$

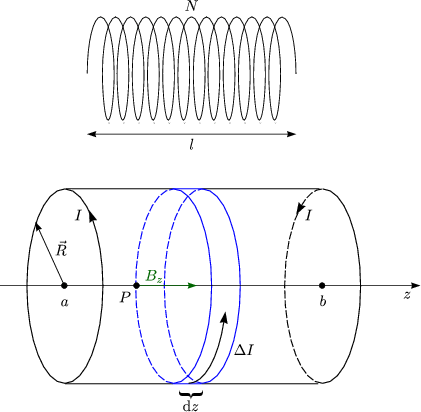
Wir knnen nun unser vorheriges Ergebnis des Magnetfeldes einer Leiterschleife benutzen, da ja eine Spule aus vielen solchen Leiterschleifen besteht:
$DI = n .I .Dz$

$2 DBz = m0-.--2pR---3-.DI 4p (z2 + R2)2$
Damit ergibt sich das Gesamtfeld am Ursprung P:
$---------------------------------- m integral b dz 1 ( b a ) | Bz = -0-.2pn .IR2 --2----2-3 = - m0 .n .I . V~ -2---2 + V~ -2--2- | 4p - a(z + R )2 2------------b-+-R------a-+-R----- [----- --]b- ----z--1- R2(z2+R2)2 -a$
Als Sonderfall betrachten wir eine sehr lange Spule (l » R):
- B_z im Zentrum (a = b): $|-------------------| |1m0nI .2 = m0 .I .N| -2---------------l--|$
- B_z auf Achse an einem Ende (a = 0): $|---------------------------| | 1 IN Bz(Zentrum) | |Bz = 2m0 .-l-= -----2----- | -----------------------------$
Unendlich langer gerader Leiter:

$m0- I .sin-hdl dB = 4p . r2$
Hierbei benutzen wir folgenden Trick als Hilfsmittel. Im Dreieck PAC stimmt die Lnge b des Bogens ber dem infinitesimal kleinen Winkel d nherungsweise mit der Dreiecksseite CA des rechtwinkligen Dreiecks CAB berein. Der eingezeichnete Winkel CBA in diesem Dreieck ist etwa so gro wie . Damit gilt also mit b = r d:
$R- rdh- sin h = r ~~ dl$
Wir lsen nach dl auf und erhalten:
$dl = r2dh R$
Oben eingesetzt gilt:
$m I dB = --0.--.sinhdh 4p R$
Durch Integration von 0 bis erhalten wir das magnetische Feld:
$integral p |----| B = m0I- sinhdh = |m0I-| 4pR 0 -2pR--$

4.1.6 Krfte zwischen zwei stromdurchflossenen Leitern

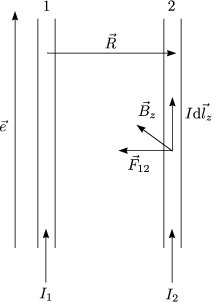
Das Magnetfeld eines Leiters 1 im Abstand R erhlt man mit der zuvor hergeleiteten Formel:

|-----------------| | m0I1 | |B1(R) = 2pR-.el× R| -------------------

Dann ergibt sich die Kraft, die der Leiter 2 im Magnetfeld des Leiters 1 erfhrt, als:

|-------------| I2 .l.m0 .I1 | l.I1I2 | F12 = I2 .l× B1 = ---2pR-----.eR = |-m0 .-2pR--eR | ---------------

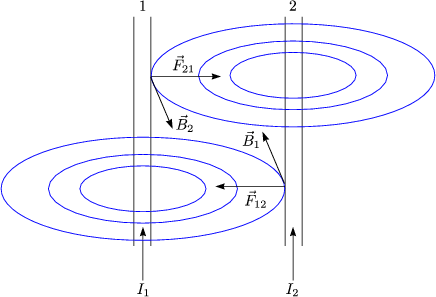
B₂ zeigt in entgegengesetzte Richtung von B₁:

|-----------------| |B2 = - m0-.I2-.e | --------2pR----l× R-

|-----------| F21 = I1 .l× B2 = + I1-.l.m0 .I2eR = m0 .l.I1I2eR|= -F12! 2pR -----2pR-----

Die beiden Krfte sind gleich gro, aber entgegengesetzt gerichtet.

Definition des elektrischen Stroms:

Wenn von 2 unendlich langen Drhten mit R = 1m zwei Stcke mit l = 1m eine Kraft F = 2 ^. 10^-7 N erfahren, fliet I = 1A.

-7 Tm F = 4p-.10---A-.1-A.1-A.1-m = 2.10-7 N 2p.1m

Demonstration:

l = 1 m

I = 15A

R = 5.10-2 m

Damit folgt fr die Kraft F:

|------| F = -225--.2 .10-7N ~~ |10-3N | 5.10-2 -------

4.1.7 Das Amp`e resche Gesetz

gf ( gf ) -q B dl = m0 .I Vergleiche: E dA = e0 P

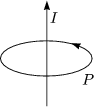
I ist die Quelle des Magnetfeldes. Das Ampèresche Gesetz ist gegeben durch:

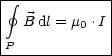
| gf -----------| | B dl = m0 .I |P | --------------

₀ ^.I ist hierbei die Quelle des Magnetfeldes. Vergleiche mit dem GAUschen Satz aus der Elektrodynamik:

|-----------| gf q | | E dA = e0| -------------

Beispiel: Stromdurchflossener Draht

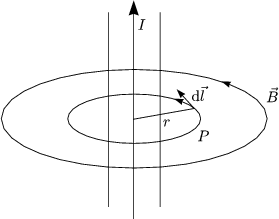
Wir hatten zuvor schon das Magnetfeld eines stromdurchflossenen Drahtes berechnet:

m0I B = 2preB

Da _B || d, ist betragsmig konstant, wenn wir als geschlossenen Weg einen Kreis whlen, dessen Mittelpunkt auf der Mittelachse des Leiters liegt und dessen Radiusvektor senkrecht zum Leiter steht. Wir ziehen daher als Konstante vor das Integral:

gf gf Bdl = m0I- dl= m0I P 2prP - - 2pr

integral i ntegral m0I- m0I- B(r1) dl+ B(r2)dl = B(r1).2pr1- B(r2).2pr2 = 2pr1.2pr1- 2pr2.2pr2 = 0 P1 P2

An diesem Beispiel wurde die Richtigkeit des Ampèreschen Gesetzes berprft.

Anwendung: Berechnung von Magnetfeldern

Stromdurchflossener Leiter:
- r > R: $gf B dl = 2prB(r) = m I 0$
  Damit gilt:
  $|-------| | m0I| B = 2pr| ---------$
- r < R: $gf B dl = m0 .I(r)$
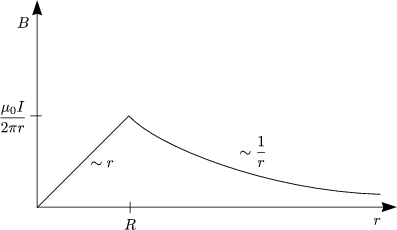
  I(r) ist hierbei der Strom durch die Querschnittsflche A(r) = r².
  $gf 2 B dl = m0 .I(r) = m0 .I .pr-2 pR$
  Damit folgt fr das Magnetfeld
  $|---------------| | --I-- | -B-=-m0 .2pR2-.r|$
- Spule mit N Windungen:
  
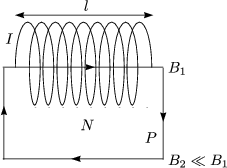
  Bei einer langen Spule knnen Randfelder vernachlssigt werden, womit nur der Beitrag des Feldes im Innern der Spule wichtig ist:
  $gf B dl = B .l != m0 .I .N P$
  
  $|----m0I-.N--| |B = -------| --------l---|$
  Wir haben hierbei angenommen, da B ber Lnge der Spule konstant ist.