4.2 Das Magnetfeld und sein Potential

[next] [prev] [prev-tail] [tail] [up]

4.2 Das Magnetfeld und sein Potential

4.2.1 Mathematischer Einschub

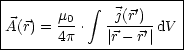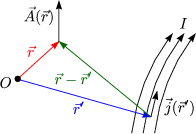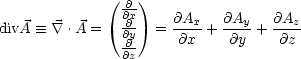
Divergenz: $(-@) @x@- @Ax @Ay @Az divA =_ \~/ .A = @y = -@x-+ -@y-+ -@z- @@z-$
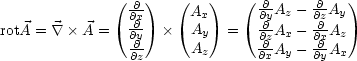
Rotation: $( ) ( ) ( ) @@x Ax @@yAz - @@zAy rotA = \~/ × A = @@y × Ay = @@zAx - @@xAz @@z Az @@xAy - @@yAx$
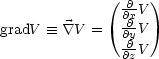
Gradient: $( @@xV ) gradV =_ \~/ V = @@yV -@V @z$

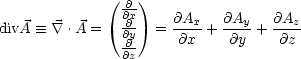
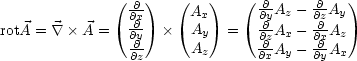
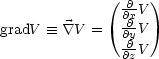
Insbesondere gilt:

$\~/$ × $( \~/ V )$ = $(\ ~/ × \~/ )$ V = 0
Konservative Felder haben keine Wirbel: $\~/$ × =
$\~/$ ^. $( ) \~/ × A$ = 0
Wirbelfelder haben keine Divergenz: $\~/$ ^. = 0

Beispiel:

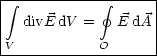
Wiederholung: GAUscher Satz des elektrischen Feldes $| integral ---------- gf -----| | divE dV = E dA | | | -V-----------O------$
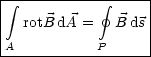
STOKESscher Satz des Magnetfeldes: $integral ---------- gf ----| | rotB dA = B ds| | | A-----------P------$

Diese beiden Stze gelten bekanntlich fr alle Vektorfelder.

Beweis des STOKESschen Satzes:

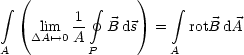
integral ( gf ) integral lim 1- B ds = rotB dA A DA'-->0 A P A

gf lim 1- B ds = rotB dA DA'-->0 A P

Fr die mehrdimensionale Taylor-Entwicklung folgt:

( ) f(x+dx) ~~ f(x)+dx. \~/ f (x) = f(x ,x ,x )+ @f(x1,x2,x3)dx + @f(x1,x2,x3)dx + @f(x1,x2,x3)dx 1 2 3 @x1 1 @x2 2 @x3 3

Man kann jede Flche im Raum in Rechtecke einteilen, die jeweils parallel zu den drei Koordinatenebenen liegen. Fr ein Rechteck, das parallel zur x₁-x₂-Ebene liegt, erhlt man:

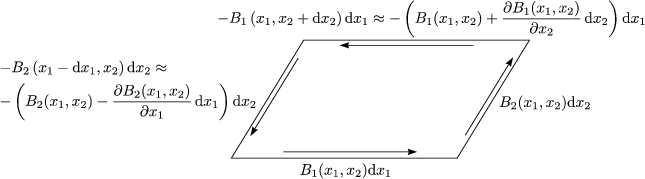
Wir integrieren entlang der geschlossenen Kurve, welche das Rechteck umschliet:

gf ( ) @B1- @B2- @B2- @B1- B ds = B1dx1+B2 dx2-B1 dx1- @x2 dx1 dx2-B2 dx2+ @x1 dx1 dx2 = @x1 - @x2 dx1dx2 P

( ) ( ) 1- gf --1--- gf --1--- @B2- @B1- @B2- @B1- Ali'-->m0 A B ds = Dlixm'-->0 DxDy B ds = Dlixm'-->0 DxDy @x1 - @x2 dx1 dx2 = @x1 - @x2 Dy'-->0 Dy'-->0

Dies ist genau eine Komponente von rot. Wenn man diese Integration noch fr Rechtecke in der x₁-x₃-Ebene und der x₂-x₃-Ebene durchfhrt, so gelangt man zu den beiden anderen Komponenten der Rotation, also von rot . Damit ist der Satz bewiesen.

4.2.2 Magnetischer Kraftflu

|------------| | integral | fm = BdA | -----A-------

Speziell fr das Magnetfeld gilt:

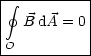
| gf ---------| | B dA = 0 | | | -O----------

Mittels des GAUschen Satzes folgt:

gf integral B dA = divB dV O V

Damit gilt also fr das Magnetfeld:

|-------| divB = 0| ---------

Es gibt somit keine Quellen und Senken im -Feld.

gf integral B dl = m .I = m . jdA 0 0

Mittels des STOKESschen Satzes gilt:

integral integral rotB dA = m0jdA

Und somit folgt:

|---------| rotB = m j| --------0--

4.2.3 Das Vektorpotential

Zur Erinnerung:

E = - \~/ V

r DV = - -- e0

Dies funktioniert nicht fr -Feld, weil aus = - $\~/$ V folgen wrde, da rot = gelte, was ein Widerspruch zum Amp reschen Gesetz darstellt. Wir machen somit einen Ansatz ber die Rotation: