Sofern der Schirm nah an der Öffnung ist, ist die Situation sehr kompliziert, weil die Amplituden der verschiedenen Elementarwellen unterschiedlich sind. Die Amplituden bei der Kugelwelle sind nämlich proportional zum Kehrwert des Abstandes:
Ist der Schirm hingegen weit weg, wenn wir also das Fernfeld betrachten, so
kann man die kleinen Unterschiede vernachlässigen. Dies ist die sogenannte
Fraunhoferbeugung. Schaut man in einer speziellen Richtung mit Wellenvektor 
, so
werden die Kugelwellen näherungsweise ebene Wellen. Somit beträgt das Feld auf
dem Schirm:
m ist die Anzahl der Elementarwellen im Spalt. In y-Richtung sei das Problem
translationsinvariant (
Spalt oder Schlitz). Für das Feld auf dem Schirm folgt
nun:
T(x) ist der Transmissionskoeffizient. Hier gilt:
Wir messen die Intensität I:
Somit ergibt sich nun, da die von t abhängige Exponentialfunktion bei der Integration wegfällt:
-
+T(x)e-ikxx ist die Fouriertransformierte von T(x).
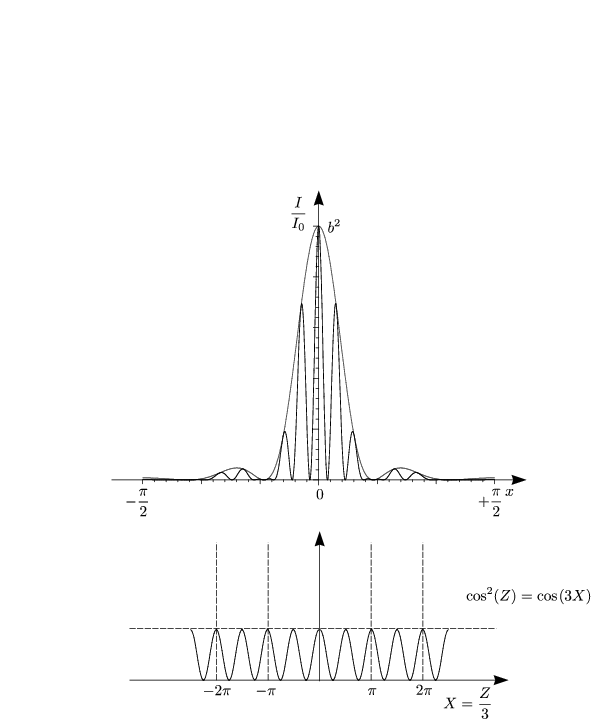
Dies ist nicht zu verwechseln mit dem Einfachspalt („umgekehrt“). Nochmals anschaulich:
Dies entspricht der Formel, welche man in der Schule kennengelernt hat. Dies erklärt aber nicht die fehlenden Maxima.
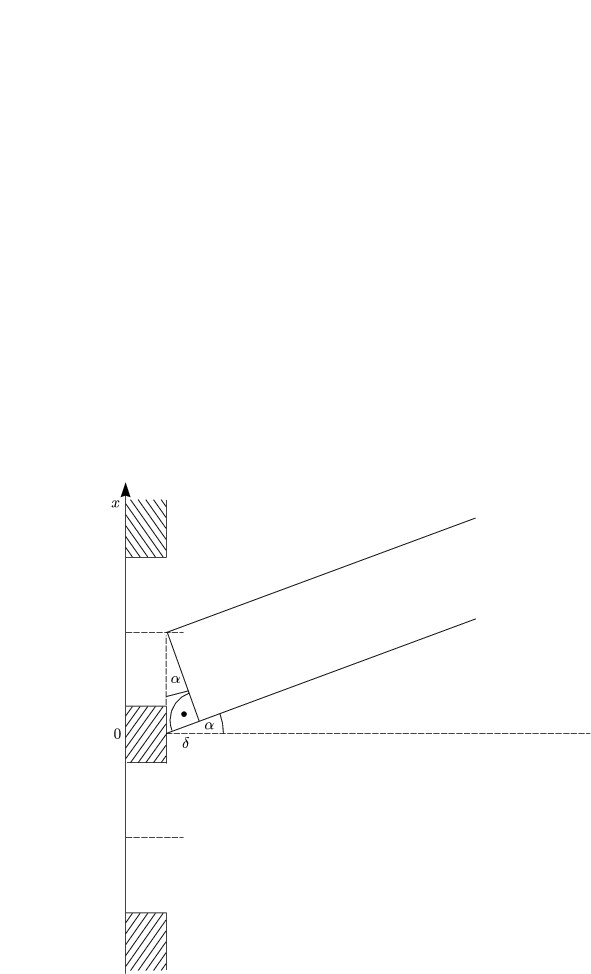
Wir betrachten folgendes zweidimensionale Problem.
Für sin
tan folgt:
Eine genauere Rechnung liefert nun:
z sei hier beliebig.
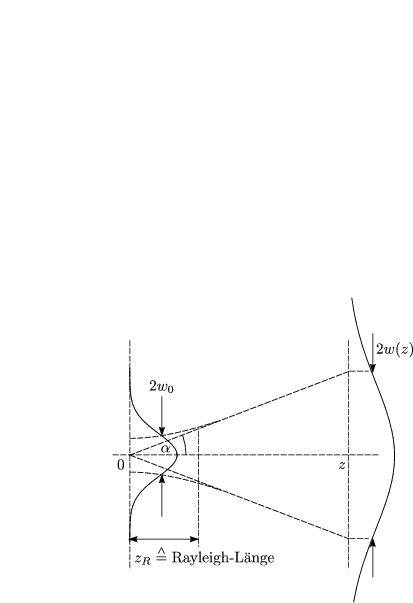
Der Öffnungswinkel berechnet sich nach:
Betrachten wir das Problem „umgekehrt“. Was ist also das kleinste erreichbare w0? Dazu lösen wir die obige Gleichung nach w0 auf:
Eine genauere Rechnung liefert:
In den meisten Lehrbüchern findet man:
NA ist hierbei die numerische Apertur:
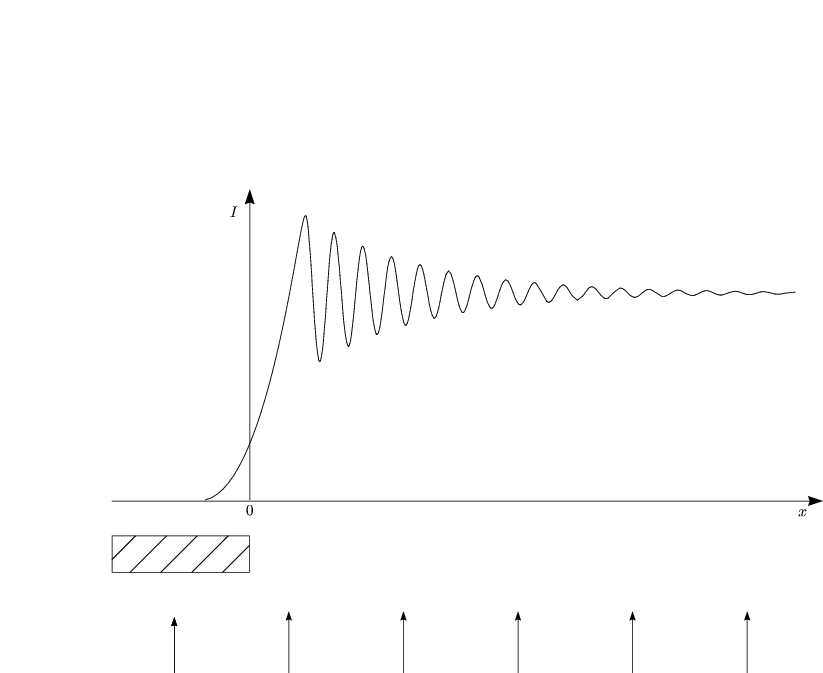
Der Limes der Fraunhoferbeugung existiert nicht! Die mathematische Beschreibung ist „im Prinzip“ einfach, nämlich die Überlagerung von Kugelwellen. Die mathematische Ausarbeitung aber ist in der Regel sehr schwierig.