
f(t) sei eine Funktion der Zeit t.

Wir betrachten zunächst der Einfachheit halber den Term e-i![]() 0t. Damit
folgt:
0t. Damit
folgt:

Was ist cos(![]() )? Die Idee ist es nun, einen konvergenzerzeugenden Faktor
einzuführen:
)? Die Idee ist es nun, einen konvergenzerzeugenden Faktor
einzuführen:
Mit Bronstein folgt für a > 0:
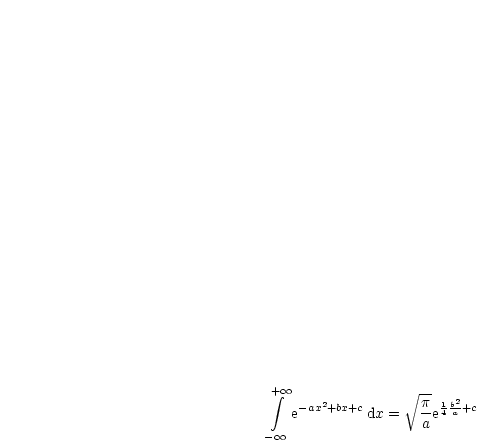
Damit folgt:


Dann ergibt sich:
Dies ist die Fouriertransformierte von f(t) = e-i![]() 0t, das heißt:
f(
0t, das heißt:
f(![]() ) =
) = ![]()
![]()
![]() ist die Fouriertransformierte von f(t) = cos(
ist die Fouriertransformierte von f(t) = cos(![]() 0t).
Wir veranschaulichen dies graphisch:
0t).
Wir veranschaulichen dies graphisch:
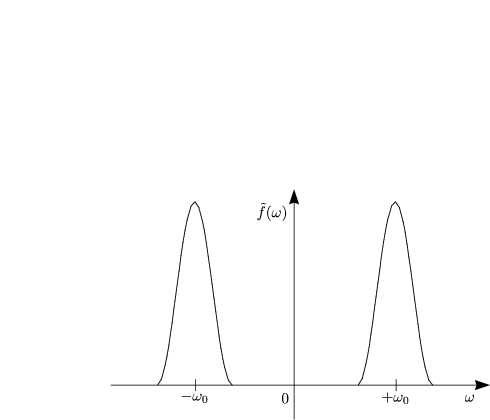
Damit gilt für periodische Funktionen f(t) mit f(t) = ![]() n=-
n=-![]() +
+![]() a
ne-in
a
ne-in![]() 0t
graphisch folgendes Ergebnis:
0t
graphisch folgendes Ergebnis:
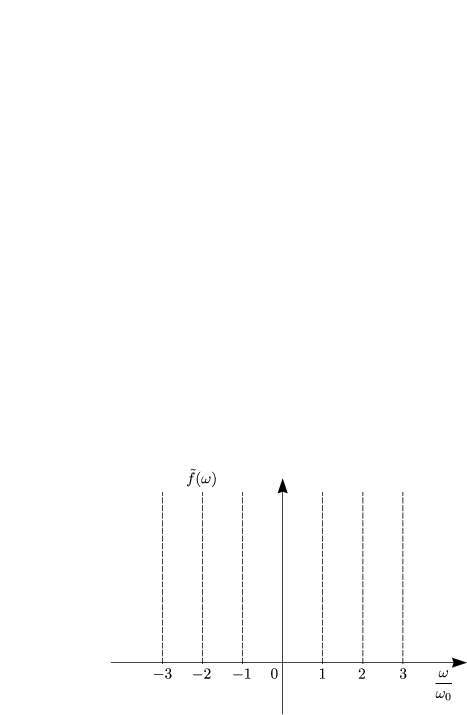
Die Fouriertransformierte einer periodischen Funktion f(t) ist die Summe
äquidistanter ![]() -Funktionen, was der Fourierreihenentwicklung entspricht. Die
Fouriertransformation ist - im Gegensatz zur Fourierreihe - auch auf nichtperiodische
Funktionen f(t) anwendbar.
-Funktionen, was der Fourierreihenentwicklung entspricht. Die
Fouriertransformation ist - im Gegensatz zur Fourierreihe - auch auf nichtperiodische
Funktionen f(t) anwendbar.


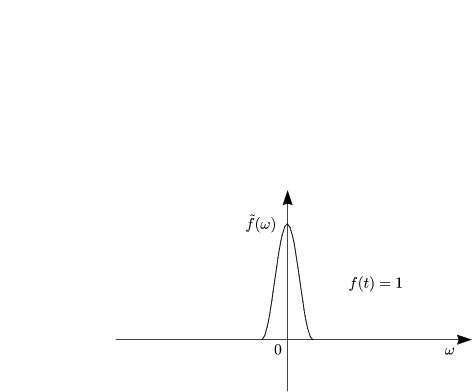
![]() (
(![]() ) sei konstant. Kann ich nun f(t) = ... auflösen? Ja, es gilt nämlich (immer
vorausgesetzt, die Ausdrücke sind konvergent):
) sei konstant. Kann ich nun f(t) = ... auflösen? Ja, es gilt nämlich (immer
vorausgesetzt, die Ausdrücke sind konvergent):

Wir wollen dies beweisen:

Wir setzen also f(t) ein und erhalten:
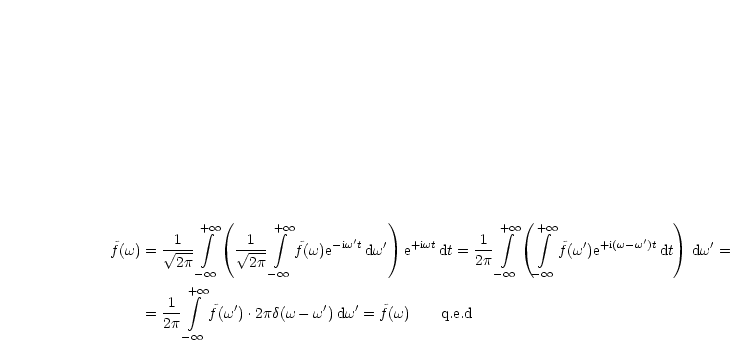 | (3.1) |
f(t) sei gegeben durch:

Dies ist die sogenannte Faltung von g und h, oft abgekürzt mit:
Dann gilt folgender Zusammenhang:
Dabei handelt es sich also um das normale Produkt von ![]() und
und ![]() (ohne
Beweis).
(ohne
Beweis).