![|----------------------------------------------------------------------|
| |
|Wir f¨uhren folgende Gr¨oße u ein, die von Frequenz und Temperatur abh¨angen soll:
| |
| Strahlungsenergie-im--Frequenzbereich-[f,f-+df-] |
|u(f,T )df := Volumen |
------------------------------------------------------------------------](ex638x.gif)
![|----------------------------------------------------------------------|
| |
|Wir f¨uhren folgende Gr¨oße u ein, die von Frequenz und Temperatur abh¨angen soll:
| |
| Strahlungsenergie-im--Frequenzbereich-[f,f-+df-] |
|u(f,T )df := Volumen |
------------------------------------------------------------------------](ex638x.gif)
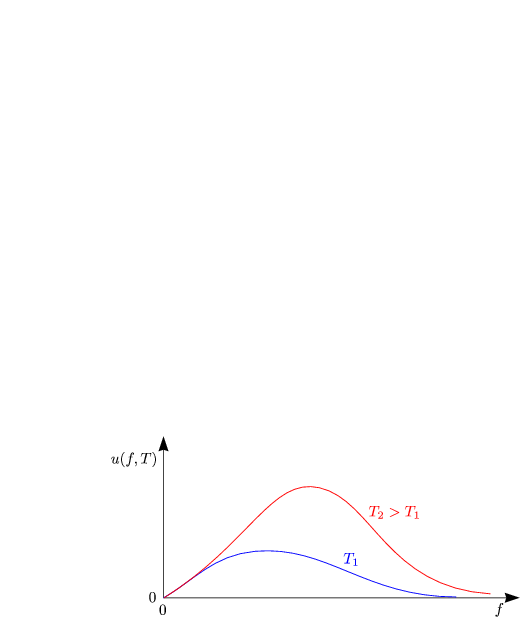
Dieses Verhalten ist unabhängig vom Material (Sonne, Ofen, etc.)! Das Plancksche Strahlungsgesetz kann im Wellenbild nicht vollständig verstanden werden.

Wir betrachten einen Würfel der Kantenlänge L, welcher innen verspiegelt ist. Die Randbedingungen sind also:
Aufgrund dieser Randbedingung kann es sich nur um eine Sinusfunktion handeln:
Berücksichtigt man alle drei Raumrichtungen, so ergibt sich:
Damit sind also schon die Randbedingungen bei x = 0, y = 0 und z = 0 erfüllt. Mit
quantisierten ![]() -Werten folgt:
-Werten folgt:
Damit sind auch die Randbedingungen bei x = L, y = L und z = L erfüllt.
Die Idee ist nun, daß ein quantisierter Zustand des Feldes einem Freiheitsgrad
entspricht. Wir erinnern uns an die Thermodynamik:

Wie viele Zustände N . df gibt es in diesem Frequenzintervall [f,f + df]?
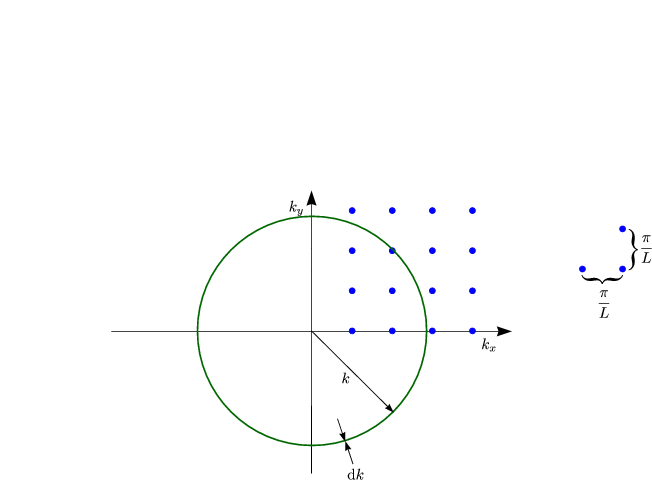
Es gilt:
Der Betrag eines ![]() -Vektors in drei Dimensionen stellt eine Kugeloberfläche dar. Die
Anzahl der Zustände ist proportional zum Volumen der Kugelschale mit dem
Volumen 4
-Vektors in drei Dimensionen stellt eine Kugeloberfläche dar. Die
Anzahl der Zustände ist proportional zum Volumen der Kugelschale mit dem
Volumen 4![]() k2 dk. Mit der obigen Gleichung resultiert für die Anzahl der
Zustände:
k2 dk. Mit der obigen Gleichung resultiert für die Anzahl der
Zustände:
Somit ergibt sich:
Dies ist das sogenannte Rayleigh-Jeans-Gesetz. Diese Proportionalität ist für kleine Frequenzen konsistent mit dem Experiment. Aber es gilt:
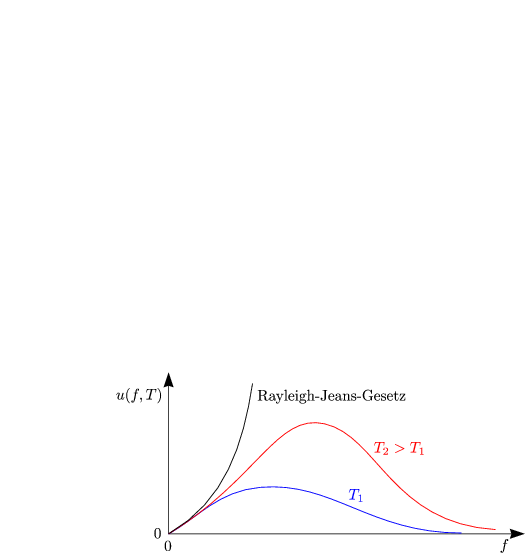
Dieses Verhalten hat lange für Aufsehen bei den Physikern gesorgt. Es konnte dann schließlich mit dem Planckschen Strahlungsgesetz verstanden werden.

Wir betrachten zwei Energieniveaus eines Mediums:

Wir kennen die Boltzmann-Verteilung schon aus der Thermodynamik:
Wir nehmen an, daß das Lichtfeld mit dem thermischen Gleichgewicht mit dem Medium ist. Wir betrachten die Änderungen im Zeitintervall dt:
dN2 ![]() Absorption von Photonen + stimulierte Emission von Photonen + spontane
Emission von Photonen
Absorption von Photonen + stimulierte Emission von Photonen + spontane
Emission von Photonen
Somit folgt:
Wohin geht die Energie beim Übergang 2![]() 1?
1?
Mit den Gleichungen (*), (**) und (* * *) folgt nun:
Somit folgt durch Auflösen nach u(f):

Wir fordern, daß für T![]()
![]() gilt:
gilt:
Dies ist genau dann erfüllt, wenn die Koeffizienten B12 und B21 gleich sind.
Es muß für f![]() 0 einen Anschluß an das Rayleigh-Jeans-Gesetz geben.
Dies zeigen wir durch Entwickeln der Exponentialfunktion in eine Reihe:
0 einen Anschluß an das Rayleigh-Jeans-Gesetz geben.
Dies zeigen wir durch Entwickeln der Exponentialfunktion in eine Reihe:
Damit gilt also:

Wir haben also das Plancksche Strahlungsgesetz erhalten.

Dann folgt für das Wiensche Verschiebungsgesetz:
Für das Stefan-Boltzmann-Gesetz gilt:


Wir führen folgende Substitution durch:
Damit folgt für das Differential df:
Dies setzen wir also ein:


Wir suchen das Maximum von u(f):
Wir setzen die Ableitung des Ausdrucks gleich Null:

Durch Umformung gilt also:
Wir substituieren folgendes:
Damit folgt die Gleichung:
Diese Gleichung kann analytisch nicht gelöst werden. Wir können x numerisch bestimmen und erhalten dann für fmax:
![---------------------------------------------------------------
| |
|p(f,T )df sei die abgestrahlte Leistung im Frequenzintervall [f,f + df].
| |
---------------------------------------------------------------](ex691x.gif)


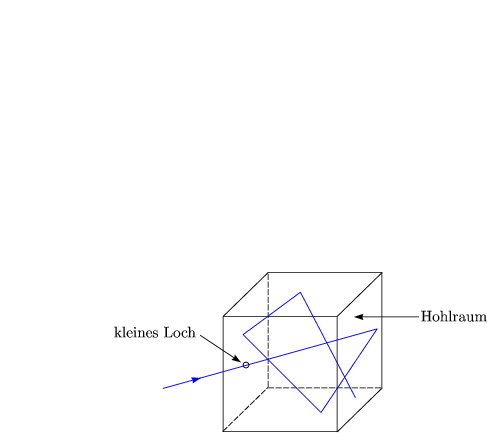
Für einen Hohlraum gilt AS(f) = 1 ![]() f. Das heißt, daß das Lich schwarz aussieht. Es
gilt weiterhin:
f. Das heißt, daß das Lich schwarz aussieht. Es
gilt weiterhin:
Wir groß ist P(f,T) für beliebige Materialien? Wir machen dazu folgendes Gedankenexperiment:
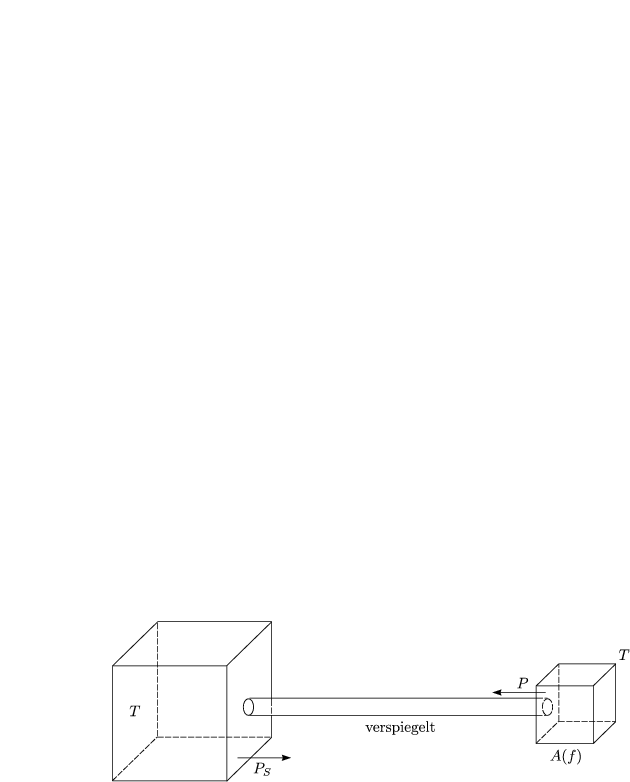
Im Gleichgewicht gilt:
Das Fazit dieser einfache Überlegung ist:
Es handelt sich um das Strahlungsgesetz von Kirchhoff. PS ist die Strahlungsleistung des schwarzen Strahlers. Ein Material, das wenig absorbiert, emittiert auch weniger als ein schwarzer Strahler.