6.2 Compton-Effekt

[next] [prev] [prev-tail] [tail] [up]

6.2 Compton-Effekt

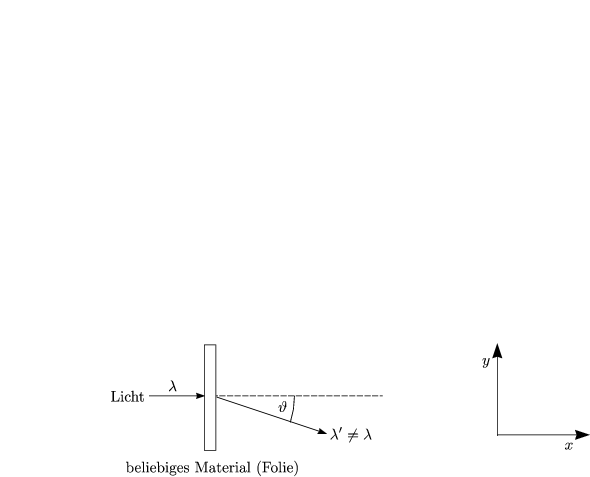
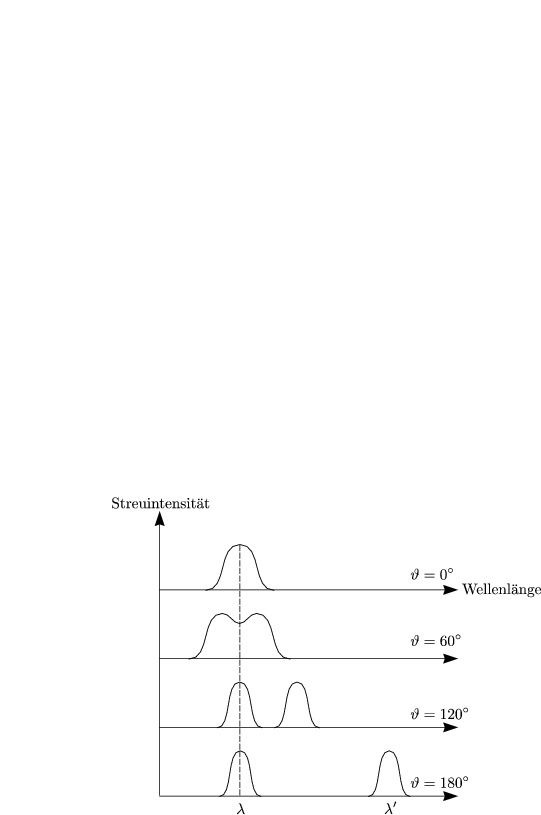
Im Experiment findet man heraus:

|----------------------------------------| |Dc = c'- c = -h--(1 -cosh) = c0(1- cosh)| --------------m0c0------------------------

Die Compton-Wellenlänge liegt ungefähr bei 2,4 ^. 10^-12 m. Der Compton-Effekt kann im Wellenbild nicht verstanden werden.

|----------------------------------------------------------------------------------------|
| |
|Derexperimentelle Befundwirdklar, wenn whir annehmen, daß dasLicht ausPartikelnbesteht, von denen|
|jedes die Energie h .f und den Impuls p = c besitzt. |
-----------------------------------------------------------------------------------------

\text{[math]}

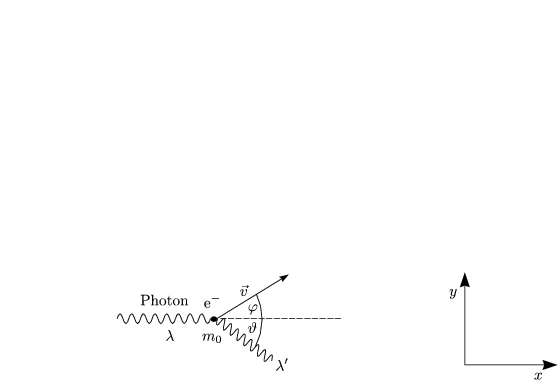
Es handelt sich um einen relativistischen Stoßprozeß.

Energieerhaltung: $2 ' 2 hf + m0c0 = hf + mc0$
Impulserhaltung:
- x-Richtung: $h-= h-cosh +mv cosf c c'$
- y-Richtung: $0 = - h-sinh + mv sin f c'$

Außerdem gilt:

c.f = c0

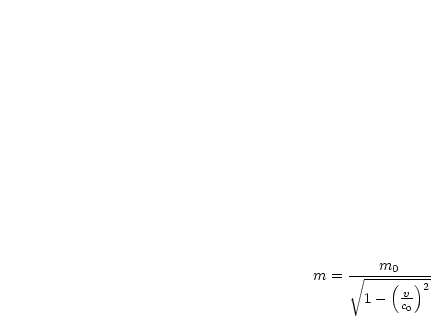
m = V~ -m0------ (v-)2 1- c0

Wir wollen nun die Beziehung herleiten. Es gilt:

h-= h-cosh + mvcosf c c'

h- c'sinh = mv sinf

Wir lösen die letzte Gleichung nach auf:

( ) f = arcsin --h--sinh c'mv

Durch Einsetzen in die erste Gleichung folgt:

V ~ ---(-----)2------ h-= h-cosh +mv 1- --h-- sin2 h c c' c'mv

Dann ergibt sich durch Quadrieren:

h2- 2-h2 cosh + h2-cos2h = m2v2 --h2sin2h c2 cc' c'2 c'2

h2 h2 h2 ( ) -2 - 2--'cosh + -'2- cos2h + sin2h = m2v2 c cc c

h2 h2- h2- 22 c2 - 2cc'cosh + c'2 = m v

( )2 2 h-- h- + 2 h-(1- cosh) = m2v2 c c' cc'

Die Gleichung für die Energieerhaltung lautet nochmals:

hc hc --0 + m0c20 = -0'-+ mc20 c c

( ) 1- 1- 2 2 hc0 c - c' + m0c0 = mc 0

( ) m = h- 1-- 1- + m0 c0 c c'

Nun gilt mittels des relativistischen Pythagoras:

( 2)2 ( 2)2 ([ ( ) ]2 ) p2 = (mv)2 =-mc0-----m0c0---= c20(m2 -m20)= c20 h- 1-- 1- + m0 - m20 c20 c0 c c'

2 2(1 1)2 (1 1 ) (mv) = h c-- c' + 2hc0m0 c-- c'

Somit folgt wieder durch Einsetzen in die ursprüngliche Gleichung:

( ) ( ) ( ) h- -h 2 -h2 2 1- -1 2 1- 1- c- c' + 2cc'(1 -cosh) = h c- c' + 2hc0m0 c - c'

( ) -h2 1- 1- 2cc'(1 - cosh) = 2hc0m0 c - c'

( ) 2-h2 (1- cosh) = 2hc m c'--c- cc' 0 0 cc'

2hc0m0(c'- c) = 2h2 (1 - cosh)

Durch Auflösen folgt schlußendlich:

|----------------------| |c'- c = -h---(1 - cosh) | ---------m0c0----------|

Dies entspricht also gerade dem experimentellen Befund.

[next] [prev] [prev-tail] [front] [up]