1.2 Was ist Licht?

[next] [prev] [prev-tail] [tail] [up]

1.2 Was ist Licht?

Licht kann als elektromagnetische Welle oder als Quanten (Photonen) beschrieben werden (Dualität). Man muß unterscheiden, ob eine Lichtquelle hell ist (physikalische Größe) oder uns hell erscheint (physiologische Größen).

Die Basiseinheit der Optik:

Lichtstärke: 1 Candela (Cd)

Abgeleitete photometrische Größen:

1 Lumen (Lm=Cdsr)
1 Lumen ist gleich dem Lichtstrom, den eine punktförmige Lichtquelle der Lichtstärke 1 Candela gleichmäßig nach allen Richtungen in dem Raumwinkel 1 sr (4) aussendet.
1 Lux (lx)=
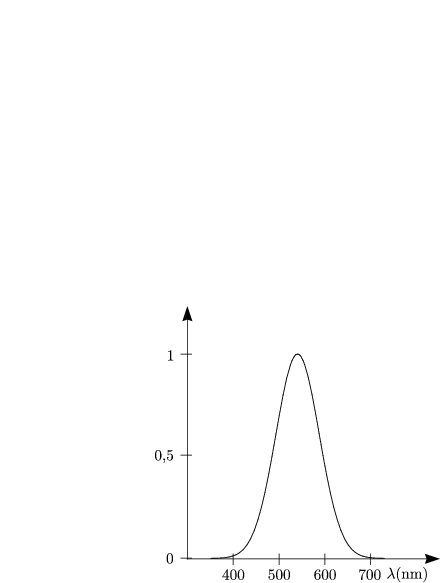
Über das Plancksche Strahlungsgesetz (schwarzer Strahler) kann 1 Candela mit der physikalischen Größe 1 Watt in Verbindung gesetzt werden. Bei einer Lichtfrequenz von 540 THz ( $/\ =$ 555 nm der Wellenlänge des Lichts $= /\$ Zitronengelb) gilt.
$|------------| | 1 W | 1 Cd = 683sr | --------------$

Beispiel:

Die Energieflußdichte, die mit der elektromagnetischen Welle verknüpft ist gegeben durch den Poynting-Vektor mit

|----------| |S = E × H | -----------

[S] = W-- m2

Bei schwachen elektromagnetischen Wellen im Vakuum gilt weiterhin:

V~ --- |E-|= m0-= Vakuumimpedanz Z0 |H | e0

V~ -m0 1,256.10-6 Z0 = e-= 8,854-.10--12- ~~ 376_O_ 0

Somit gilt nun:

V~ -- 2 e0- |S|= |E| m0 mit S ||k

Oszilliert mit der Frequenz , so oszilliert auch ||. Mittelt man über diese zeitliche Oszillation, spricht man von der Intensität I des Lichts.

|---- V~ -------------| | 1 e0- 2 2 | I = 2 m0 |E | oc |E || --------------------

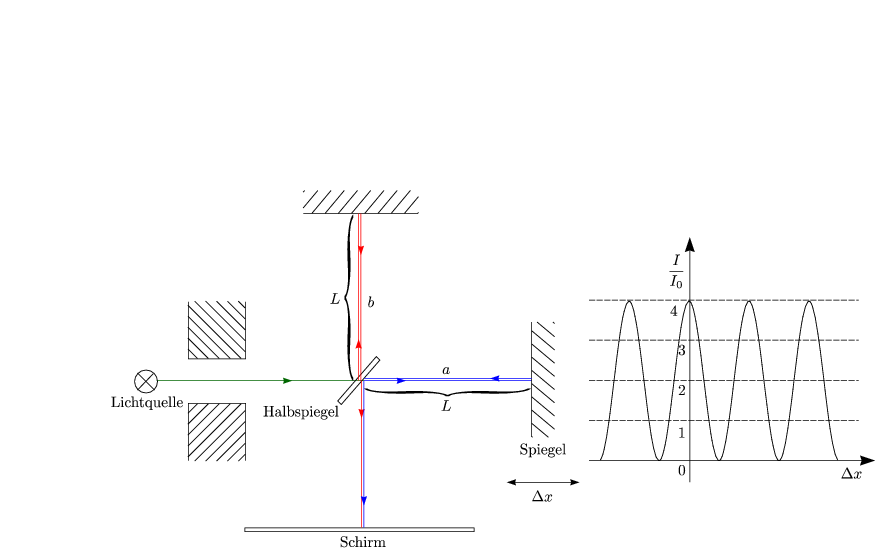
Das Licht einer Glühlampe weist eine endliche Kohärenzzeit auf und eine unendliche Kohärenzlänge.

--Koha¨renzl¨ange--- Koha¨renzzeit = Lichtgeschwindigkeit

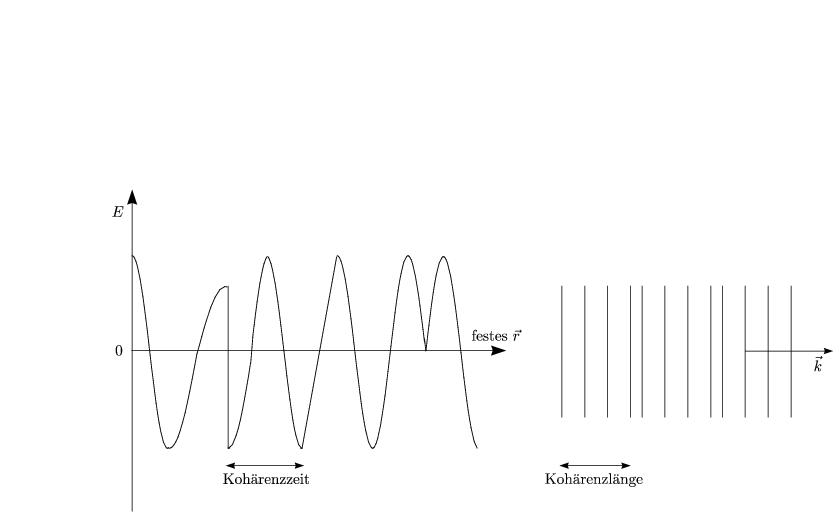
Oder auch:

Michelson-Interferometer:

Glühlampe:

Wiederholung:Maxwellsche Gleichungen

Das System aus Differentialgleichungen, welches die Maxwellschen Gleichungen beinhaltet, lautet:

@-
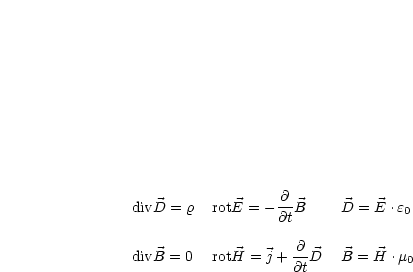
divD = r rotE = - @tB D = E .e0

divB = 0 rotH = j + @-D B = H .m0
@t

In Medien gilt:

r = rint + rext

j = j +j int ext

j_int ist fast nie von Bedeutung in der Optik.

dive0E = rint + rext

dive0E - rint= rext divP

( ) div e0E + P = rext --- --- D

Also gilt nun:

|------------------------------------|
| |
|D = rext (wobei rext oft weggelassen wird)
| |
| 1-( ) |
|E = e0 D -P |
| |
|divP = - rint |
--------------------------------------

wird Polarisation genannt. Die Einheit der Polarisation ist:

As As.m Dipolmoment [P ] = [D] =--2 = ---3-- /\ =------------ m m Volumen

In steckt die gesamte Information über die optischen Eigenschaften des Materials. Demnach verwendet man meistens auch andere Größen:

e,x,n,a,...

Zur Erinnerung:

Der Poynting-Vektor . Energiedichte des elektromagnetischen Feldes w:

( ) w = 1 D .E + B .H ;[w] =-J- 2 m3

Wir berechnen die zeitliche Änderung von w ( $= /\$ Zu- oder Abflüssen + Umwandlung)

@w 1( ˙ ˙ ˙ ˙) -@t = 2 D .E +D .E + B .H + B .H

Im Vakuum gilt mit den Maxwellschen Gleichungen = ₀ und = ₀:

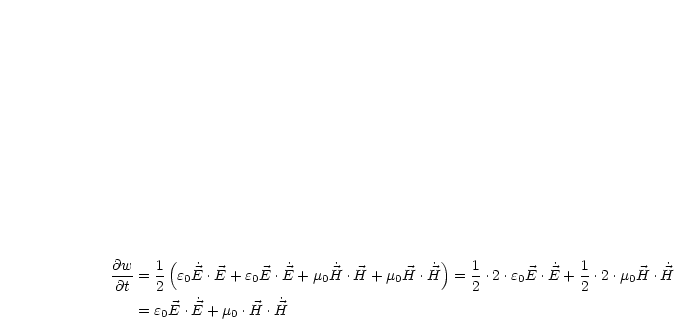( ) @w-= 1 e0E˙.E + e0E .E˙+ m0H˙.H + m0H .H˙ = 1 .2.e0E .˙E + 1.2 .m0H .˙H @t 2 2 2 = e0E .E˙+ m0 .H .H˙

(1.1)

Nun gilt ja:

|-------------------------| | ˙ ˙ | \~/ -×-E-=---B-==>-B-=--- \~/ -×-E

|------------------------------| - \~/ -×-H-=-j-+-˙D-==>-D˙=- \~/ -×-H---j

Wir setzen dies oben ein und erhalten:

( ) ( ) @w-= e0E .E˙+ m0 .H .H˙= E .D˙+ H .B˙= E \~/ × H -j - H \~/ × E @t

Mit div = - ^. $( ) \~/ × b$ + ^. $( ) \ ~/ ×a$ erhält man schlußendlich:

( ) @w-= - div E ×H - j .E =: S @t

Also folgt:

|@w----------------| |-@t = -divS- j .E | -------------------|

/\ divS = Abschaltung

j .E /\ = Umwandlung in Wa¨rme (Ohmsches Gesetz)

Beispiel:

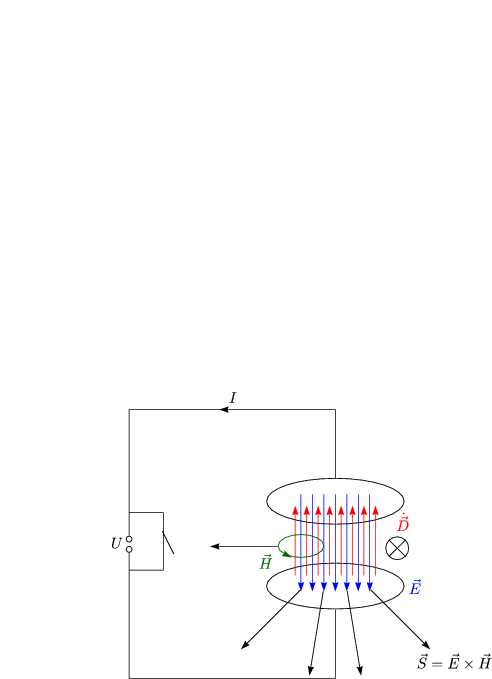
Der Poynting-Vektor zeigt also die Richtung des Energieflusses an. Der Betrag gibt die Größe des Energieflusses an.

[next] [prev] [prev-tail] [front] [up]