1.3 Der eindimensionale Lorentz-Oszillator

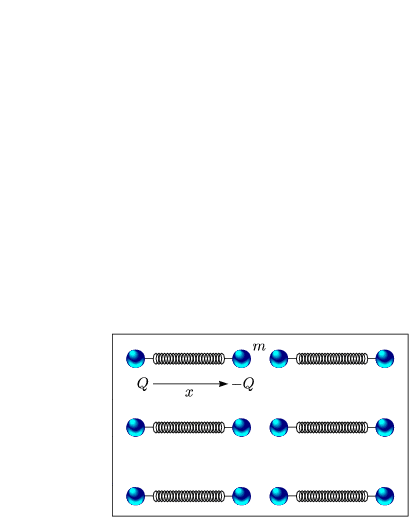
Im Volumen V befinden sich N Oszillatoren. Das Dipolmoment p eines Oszillators ist:

Damit wird die Polarisation zu:

Die Newtonschen Bewegungsgleichungen sind:

Die nichtlinearen Terme werden vernachlässigt, da die Auslenkungen sehr klein sind, und wir erhalten:

Dies ist der harmonische Oszillator, d.h. E ist klein und x ist klein. Das Hookesche Gesetz gilt. Abweichungen davon gibt es jedoch in der nichtlinearen Optik (siehe Kapitel 7.1).
Mit E = E₀ cos(t) und x = x₀ cos(t) folgt:

Oder mit der Eigenfrequenz = ergibt sich:

Daraus resultiert die Polarisation des Mediums:

Mit der optischen Suszeptibilität ():

Mit D = ₀E + P folgt weiterhin:

Der Index r bei _r wird oft weggelassen. () ist die optische dielektrische Funktion.

Also ist:

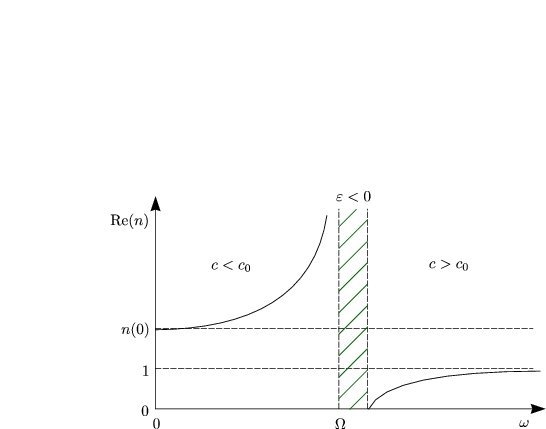
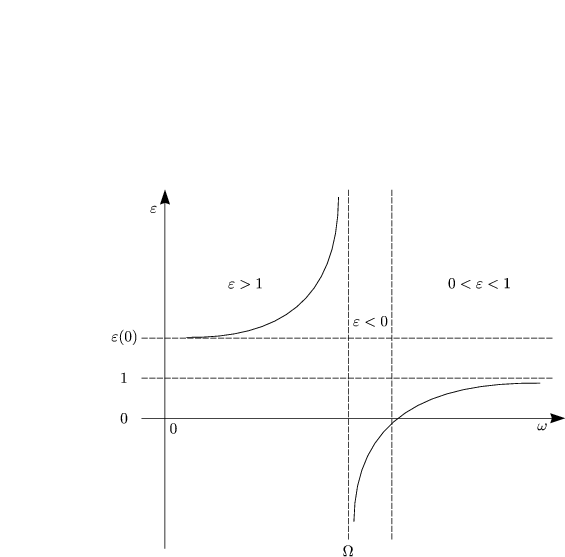
Wir veranschaulichen das Verhalten graphisch:

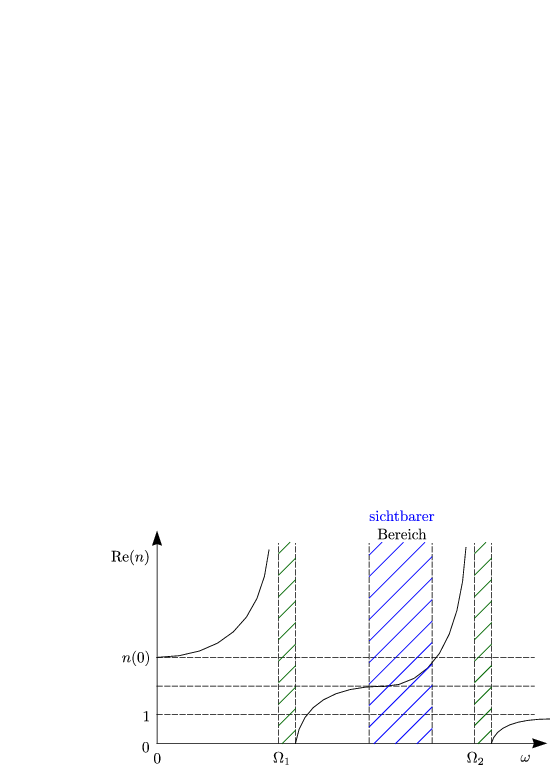
Oft gibt es nicht nur eine, sondern mehrere Resonanzen. Wir tragen auch dies wieder graphisch auf:

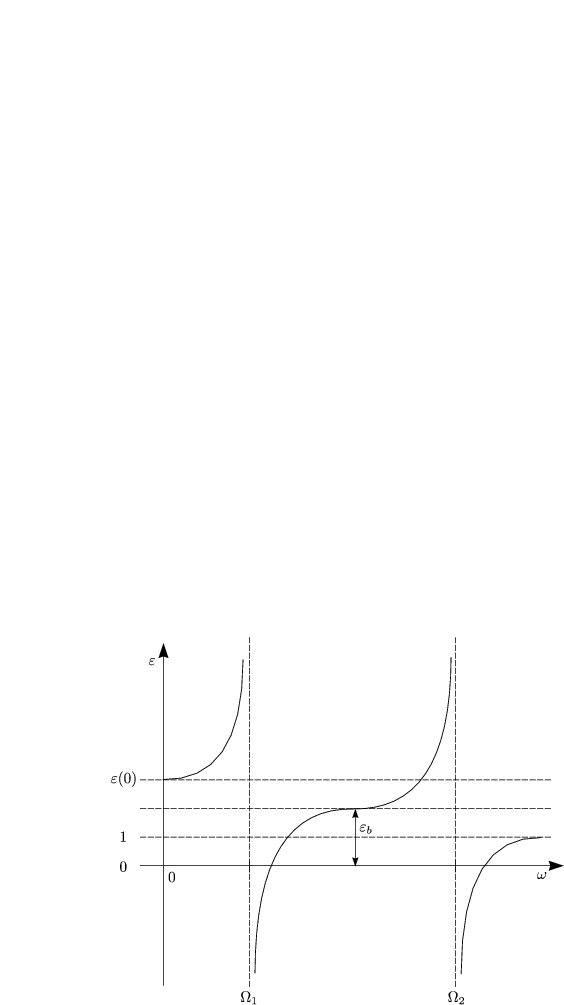
Will man höherfrequente Resonanzen(hier nur ₂) zusammenfassen, so schreibt man mit der Hintergrund-Dielektrizitätskonstante _b:

In unserer Schreibweise bezieht sich das nur noch auf die Resonanz 1. Aus den Maxwell-Gleichungen folgt die Wellengleichung mit der Mediumlichtgeschwindigkeit c.

Die Mediumlichtgeschwindigkeit ist:

Die Vakuum-Lichtgeschwindigkeit hat folgende Größe:

Also folgt für die Brechzahl:

Graphisch (für Resonanz):

Graphisch (für mehrere Resonanzen):