Die komplexe Wellengleichung lautet:
Sofern hier gilt:
Diese Beziehung ist die sehr wichtige Dispersionsrelation. Diese setzen wir in die Wellengleichung ein und erhalten:
Mit
n = n' + in'' folgt:
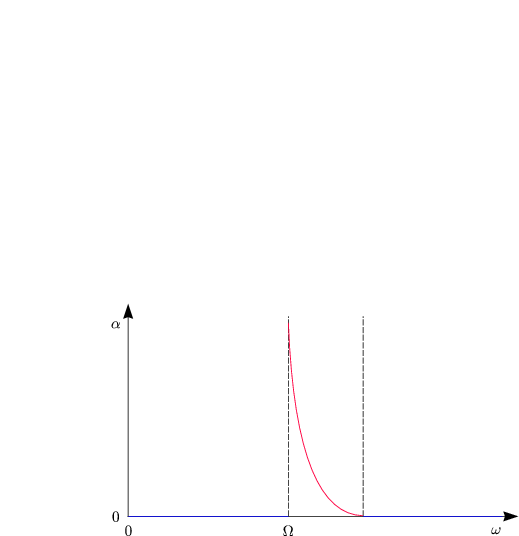
Es handelt sich also um eine ebene Welle, die mit dem Absorptionskoeffizienten 
exponentiell gedämpft ist:
n'' ist hierbei der Imaginärteil der Brechzahl. Die Intensität einer elektromagnetischen Wellen ist ja gegeben durch:
Daher kommt das 
im Absorptionskoeffizienten.
