8.3 Das ideale Gas

Definition:

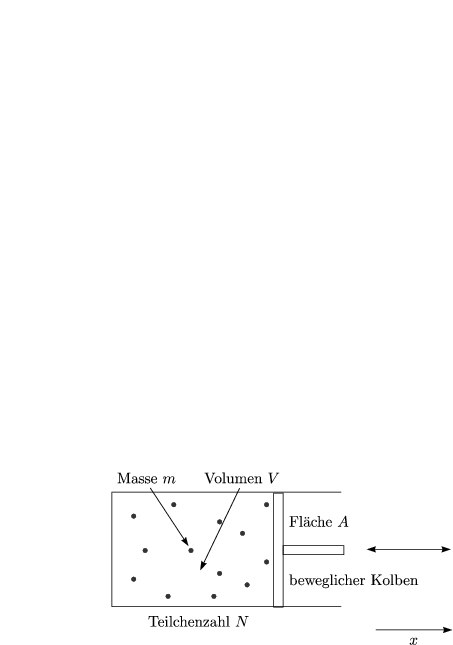
Ein ideales Gas ist eine große Anzahl von Teilchen (z.B. Atome oder Moleküle), deren gegenseitige Wechselwirkung klein aber nicht verschwindend ist. Normale Gase erfüllen diese Bedingung bei nicht zu niedrigen Temperaturen gut.

Ziel:

Verknüpfung der Zustandsgrößen p, V , T, N

Zur Erinnerung:

Betrachten wir ein Zeitintervall dt:
Wie groß ist der Kraftstoß F_x dt? Haben die Teilchen zum Beispiel den Impuls p_i,x, gilt:

Es heißt hier 2p_i,x aufgrund der Impulserhaltung, da das Teilchen die Richtung ändert. dN₁ ist die Zahl der Teilchen, die im Zeitintervall dt mit dem Stempel stoßen, also dx vom Stempel entfernt sind (Dreisatz).

Der Faktor kommt daher, weil sich die Hälfte der Teilchen nach rechts und die andere nach links bewegt.

Es resultiert der folgende Druck:

Daraus folgt nun p_i,x:

Summation über alle Impuls p_i,x ergibt nun:

Beziehen wir die klassische Mechanik mit ein, so folgt für die kinetische Energie:

Aufgrund der Symmetrieeigenschaften ist keine Richtung von x, y und z ausgezeichnet. Daraus folgt das sogenannte Gleichverteilungsgesetz.

Oder auch mit der mittleren kinetischen Energie _kin geschrieben:

Daraus folgt:

Das Produkt p ^. V hängt somit nicht von der Verteilungsfunktion ab.