9.4 Expansion idealer Gase

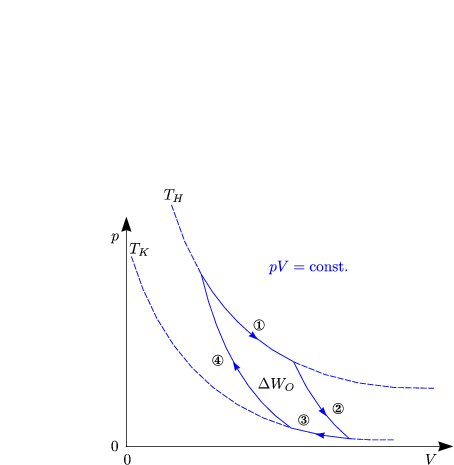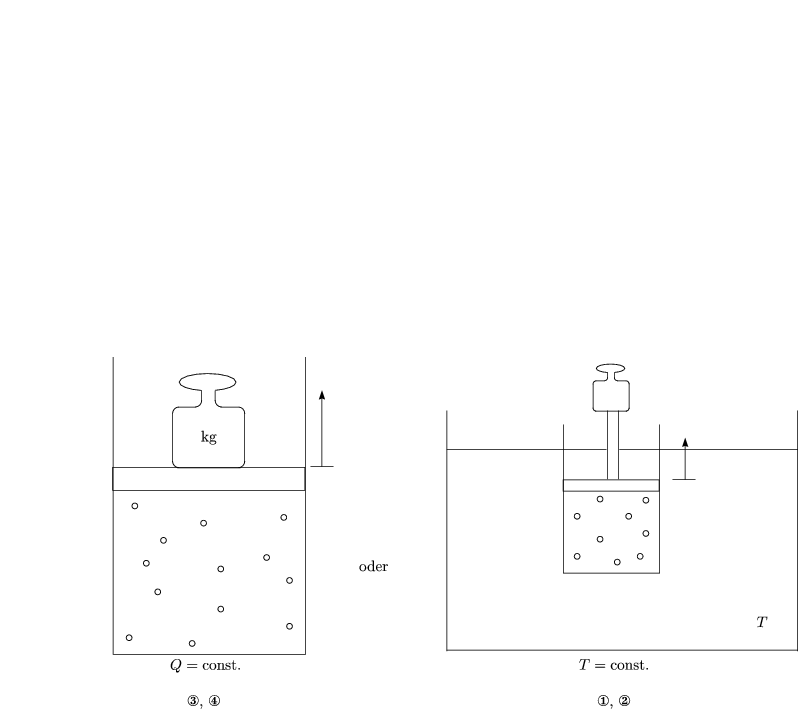
Wir betrachten vier Grenzfälle:

1. Reversible, isotherme Expansion idealer Gase

   Dies folgt nach dem 2.Hautpsatz. Durch Integration folgt:

   

   Mit der Zustandsgleichung des idealen Gases pV = nRT ergibt sich:

   
   

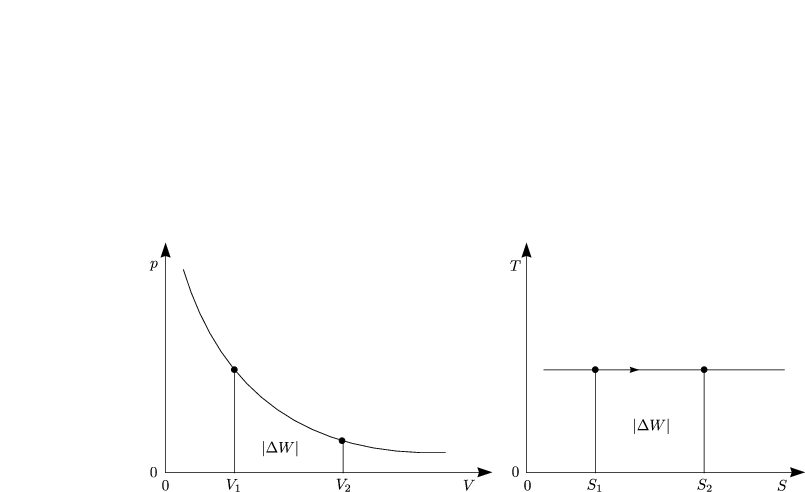
   Für V ₂ > V ₁, d.h. für Expansion des Gases, gilt W < 0, das Gas leistet also Arbeit.

   Merkregel für Vorzeichen:

   
   

   Diese Energie kommt aus dem Wärmebad, das dafür sorgt, daß die Temperatur des Gases konstant ist. Das Gas hat also nur die Rolle eines Vermittlers. Seine innere Energie ist nRT = const. bleibt unverändert, nur seine Entropie steigt an. Das ist grundverschieden von der Expansion einer Hookeschen Feder, bei der eben die Energie, die das Gewicht gewonnen hat im Schwerefeld der Erde, aus der Feder kommt.

   Veranschaulichung im pV - bzw. TS-Diagramm:

   

2. Vollständig reversible isotherme Expansion idealer Gase

   Wir nehmen an, daß das Gewicht beispielsweise plötzlich weggerissen wird. Dann ist die Kraft gleich 0 und damit auch die zu leistende Arbeit.

   

   Wir vom ersten Hauptsatz zu erwarten war. Mit dU = W + Q folgt:

   
   

3. Vollständig irreversible adiabatische Expansion idealer Gase

   Siehe 2.

   

   Mit dU = nRT = W + Q folgt:

   
   

4. Reversible adiabatische (isentropische) Expansion idealer Gase

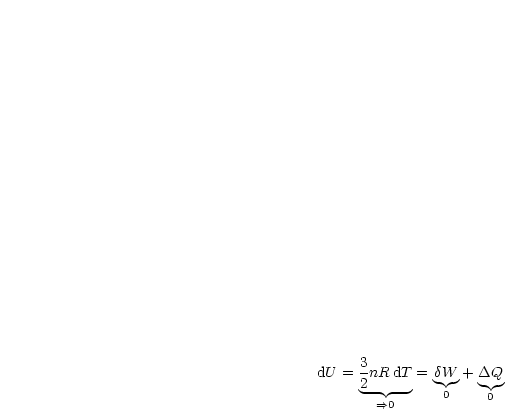
   Wir halten zuvor noch eine Kleinigkeit fest:

   

   

   

   Mit der Zustandsgleichung des idealen Gases pV = nRT folgt:

   

   Durch Integration von Anfangs- bis Endzustand resultiert:

   

   Daraus ergibt sich nun durch exponieren:

   

   Hieraus folgt offensichtlich:

   

   Der Exponent ist gleich - 1. Nun setzen wir nochmals die ideale Gasgleichung ein:

   

   Wir fassen dies in folgender Form zusammen:

   

   Dies ist die sogenannte Adiabatengleichung des idealen Gases.

   

Arbeit W:

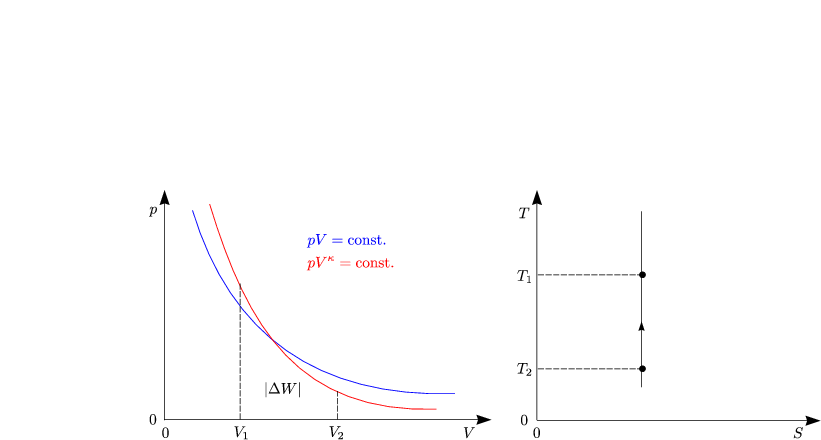
Damit folgt die Arbeit:

In diesem Fall kommt die Energie, die der geleisteten Arbeit entspricht, es kühlt sich ab. Seine Entropie bleibt konstant.

9.4.1 Der Carnotsche Kreisprozeß

Technisch relevante Maschinen verwenden Kreisprozesse, d.h. nach einen Arbeitszyklus nimmt die Maschine wieder den gleichen thermodynamischen Zustand an. Interessant ist folgendes:

Dieses Prinzip wird beispielsweise in Motoren, Wärmepumpen, Kühlschränken usw. benutzt. Der 1.Hautpsatz verbietet unmittelbar periodisch arbeitende Maschinen, die nichts tun, als mechanische Arbeit zu liefern. Wegen dU = 0 nach einem Zyklus und mit Q = 0 ergibt sich:

Eine solche Maschine nennt man Perpetuum Mobile 1.Art.

Der erste Hauptsatz alleine verbietet jedoch nicht ein Perpetuum Mobile 2.Art. Dies ist eine periodisch arbeitende Maschine, die nicht tut als ein Wärmebad abzukühlen und mechanische Arbeit zu leisten (dU = 0 = Q + W).

Veranschaulichung eines beliebigen Kreisprozesses:

1. Reversible, isotherme Expansion einer Arbeitssubstanz bei einer hohen Temperatur T_H
2. Reversible, adiabatische Expansion einer Arbeitssubstanz auf eine niedrigere Temperatur T_K
3. Reversible, isotherme Kompression einer Arbeitssubstanz bei der niedrigen Temperatur T_K
4. Reversible, adiabatische Kompression einer Arbeitssubstanz auf die hohe Temperatur T_H

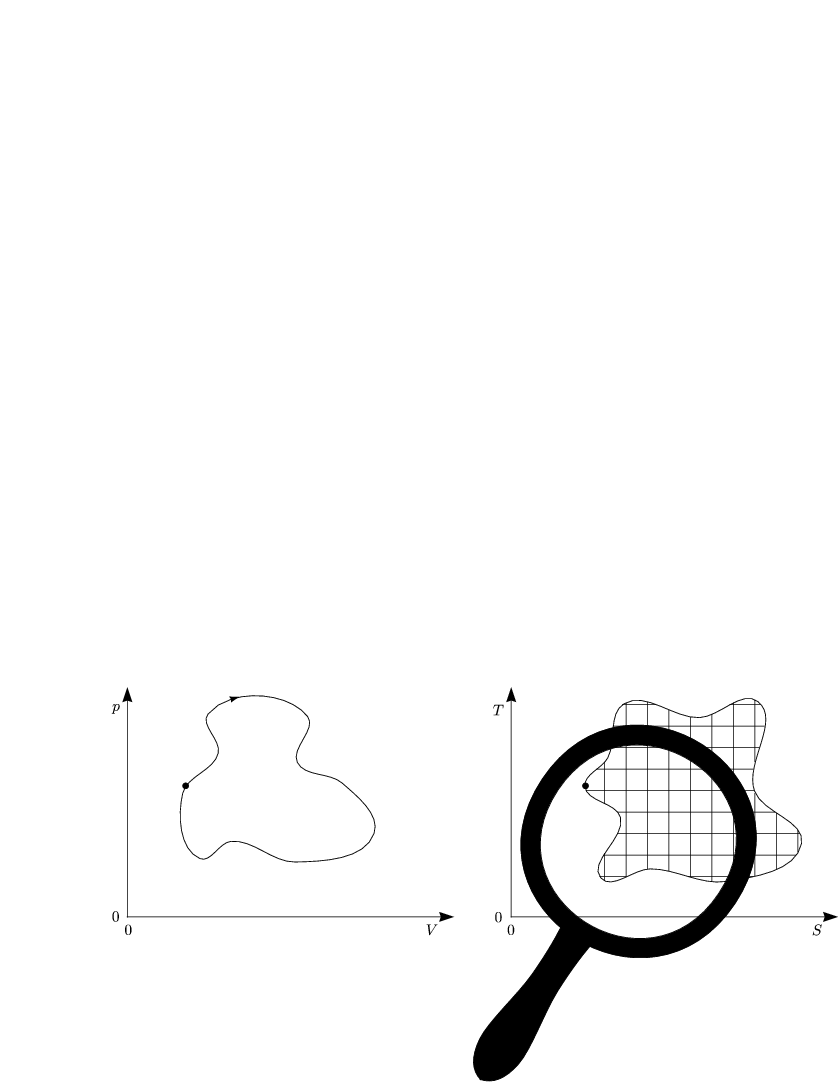
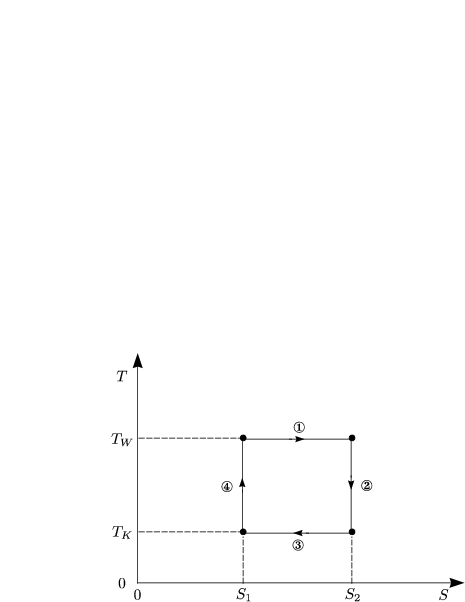
Die Arbeitssubstanz kann ein ideales Gas sein - muß aber kein ideales Gas sein. Für einen Zyklus gilt:

Damit ergibt sich, da Q bei adiabatischen Prozessen 0 ist:

Die im Schritt 1 geleistete mechanische Arbeit kommt aus dem heißen Wärmebad mit Temperatur T_H. Wir konvertieren jedoch wieder mechanische Arbeit in Wärme in Schritt 3, das Wärmebad mit der Temperatur T_K wird aufgeheizt (außer, falls T_K = 0). Wärme wird damit im allgemeinen nicht vollständig in mechanische Arbeit umgewandelt. Wie groß ist der Wirkungsgrad?

Definition:

Dies ist der sogenannte Wirkungsgrad. Mit Q_H = T_H > 0 ergibt sich der Wirkungsgrad des Carnotschen Kreisprozesses bei reversibler Prozeßführung:

Bei reversibler Prozeßführung gilt:

Mit dem Wirkungsgrad folgt:

Mit Q_H^irrev < Q_H^rev > 0 folgt, daß der Bruch dem Betrage nach größer wird bei irreversibler Prozeßführung. Mit Q_K^irrev < Q_K^rev < 0 ergibt sich dann noch, daß der Bruch bei irreversibler Prozeßführung negativer wird:

Dies ist der Wirkungsgrad des Carnotschen Kreisprozesses bei beliebiger Prozeßführung. Wählt man nur ein Wärmebad, d.h. T_H = T_K, folgt daraus, daß = 0 ist. Es ist also nicht möglich, eine periodisch arbeitende Maschine zu bauen, die nichts tut als ein Wärmebad abzukühlen und mechanische Arbeit zu leisten, obwohl dies dem Energieerhaltungssatz überhaupt nicht widersprechen würde.

Dies ist eine Folge des 2.Hauptsatzes (und des 1.Hauptsatzes).

Beispiel:

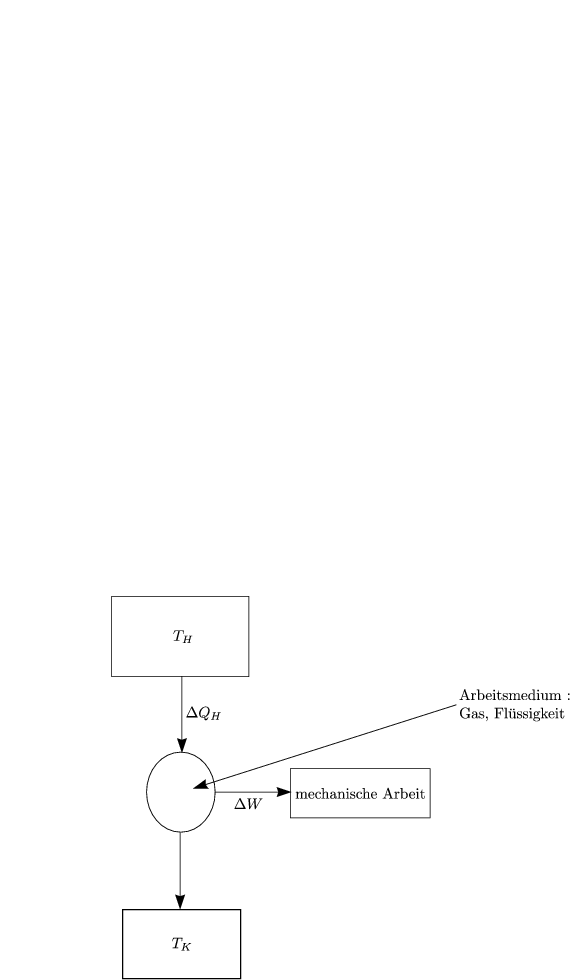
Die Arbeitssubstanz sei ein ideales Gas.