10.1 Die Van-der-Walls-Zustandsgleichung

Im Gegensatz zum idealen Gas wollen wir jetzt die Wechselwirkung der Gasmoleküle explizit berücksichtigen. Wir idealisieren die Gasmoleküle als Kugeln mit Radius r und Querschnitt = r² ( $/\ =$ Wirkungsquerschnitt):

Mittlere freie Weglänge l:

Bewegt sich ein Molekül um die Strecke l, hat es ein Volumen l ^. überstrichen (falls r « l). Dann folgt die Zahl der Moleküle in diesem Volumen mittels Dreisatz:

N- (l.s) V

Wird diese Zahl 1, so findet im Mittel ein Stoß statt. Damit folgt die mittlere freie Weglänge:

|----------| |l = (-1)---| -----NV--.s-|

Zustandsgleichung:

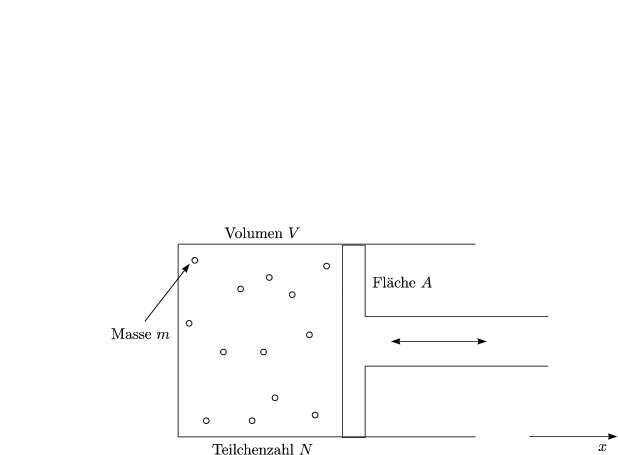
Wieder betrachten wir ein Zeitintervall dt. Wir groß ist der Kraftstoß F_x dt auf den Stempel? Haben die Teilchen beispielsweise den Impuls p_i,x, so gilt:

|-----------------| |Fi,x dt = 2pRi,axnddN| I ------------------

Der Faktor 2 rührt vom Impulserhaltungssatz her, da das Teilchen beim Stoß ja die Richtung ändert. Die Wechselwirkung hat zwei Effekte:

Im Gas wirken im Mittel keine Kräfte, am Rand aber schon!

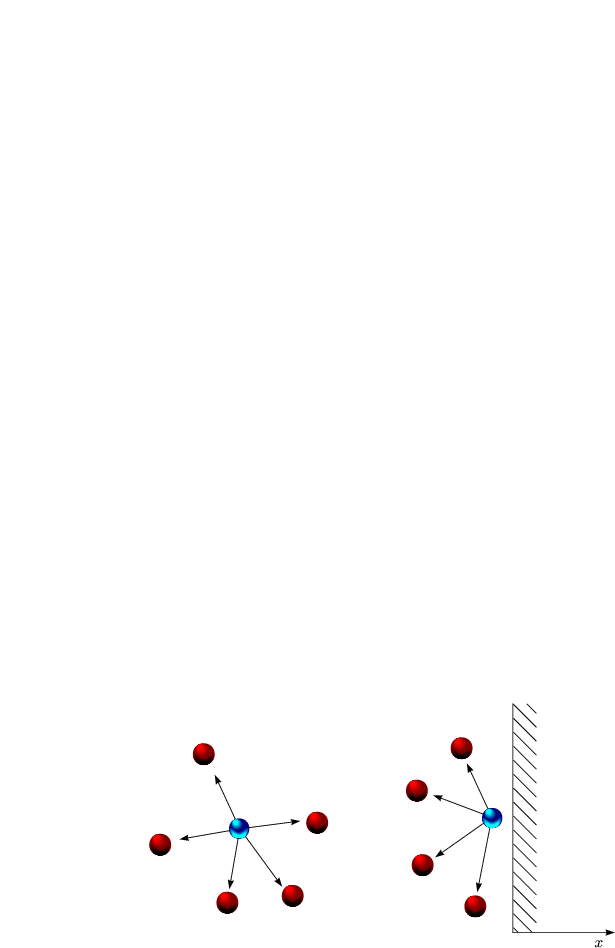
Die Dicke des Randes sei d. Dann wirkt die Kraft:
$(N ) F ~~ a V-$
ist eine Proportionalitätskonstante, die materialspezifisch ist. Das Molekül ist für eine bestimmte Zeit in dieser Randzone. Somit reduziert sich sein Impuls und man erhält:
$|-------------(---)-----| pRand = p - a N- -d- | II |i,x i,x V vi,x | ------------------------$
Die Zahl der Teilchen dN_i, die im Zeitintervall dt mit dem Stempel stoßen, folgt wieder durch den Dreisatz: $dNi= 1dV-= 1dL-.A- Ni 2 V 2 V$
Der Faktor kommt daher, weil sich die eine Hälfte der Teilchen nach links und die andere nach rechts bewegt.

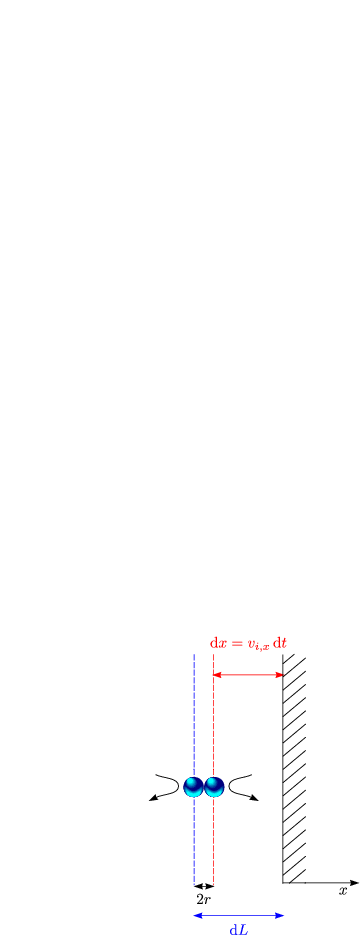
Ohne Stöße würde ein Molekül im Zeitintervall dt die Strecke dx zurücklegen. Für einen zentralen Stoß entlang der x-Achse zweier Teilchen mit entgegengesetztem Impuls verlängert sich die Strecke effektiv auf dx + 2r.
Im Mittel erfährt das Molekül auf einer freien Weglänge l einen Stoß; es gilt also folgendes:
$( ) 2r l '--> l+ 2r = l 1+ l$
Für beliebige Stöße reduziert sich dies nun um einen Faktor < 1:
$( 2r) l '--> l 1 + b-l$
Also folgt damit:
$( 2r) ( 2r) p ( 2r) dL = dx 1+ b -- = vi,xdt 1 + b-- = -i,x dt 1 + b-- l l m l$
Damit wird:
$( ) dNi = Ni .1 A-.pi,xdt 1+ b 2r 2 V m l$

\text{[math]}

Die Effekte 1 und 2 führen also nun durch Einsetzen von II und III und I zu:

( (N-) -d- ) 1A- pi,x ( 2r) Fi,xdt = 2 pi,x- a V vi,x .Ni 2V . m dt. 1 + b l

( ( ) ) ( ) Fi,x = pi,x- a N- -d- .Ni A-.pi,x . 1+ b 2r V vi,x V m l

Somit wird der Druck p_i = :

( ( ) ) ( ) pi = pi,x - a N- d.m-- .Ni-1pi,x . 1 +b 2r V pi,x V m l

Summation über alle Impuls p_i,x ergibt:

( ( ) ) ( ) sum N- d.m-- 1-pi,x 2r p = Ni pi,x - a V pi,x .V m 1+ b l i

[ 2 ( ) 2 ( ) ] p = sum N 1-pi,x - a N- d.m-.1--.pi,x + 1-pi,x.b 2r- a N- d.m--1-.pi,x.b 2r i i V m V pi,x V m V m l V pi,x V m l

[ ] p = sum N 1-p2i,x - a.N--.d+ -1.p2i,x.b 2r- a .b .N-.d.2r i i V m V 2 V m l V 2 l

Der zweite und vierte Term hängen nicht mehr vom Summationsindex i ab. Wir können diese somit von der Summe abspalten und erhalten:

[ ] N-.d- N-.d- 2r sum -1p2i,x 1- p2i,x 2r p = - N .a . V2 -N .a.b . V2 . l + Ni V m + V . m .b l i

und sind Zahlenwerte, die eine sehr kleine Größenordnung besitzen. Infolgedessen kann der Term proportional zu d ^. ^. « 1 vernachlässigt werden, wobei dann folgt:

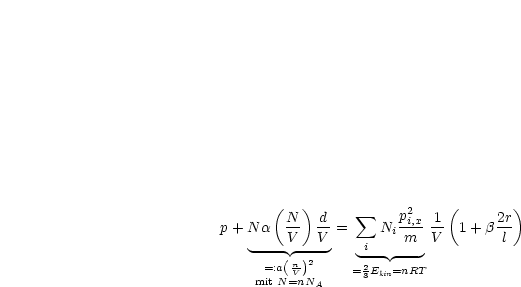
( ) ( ) N- d- sum p2i,x 1- 2r p+ N a V V = Ni m V 1 + b l ---- --2- -i- --- =:a(Vn) =23Ekin=nRT mit N=nNA

( ) (n--)2 1- 2r p+ a V = nRT .V 1 +b l

Weiterhin gilt für kleine x:

1 + x ~~ -1---f¨ur x« 1 1- x

Damit ergibt sich:

( 2r) ( 2r)- 1 1 +b -- ~~ 1 - b-- l l

Mittels dieser Beziehung folgt nun:

( (n )2)( 2r) p+ a V- V - V b-l = nRT

Wir schreiben nun:

V b2r = Vb -2r1-- ~ r3 = 2b .r .s.N = (2b .r.s .NA).n =: n.b l (NV ).s

Damit folgt das Endergebnis:

|(-----(--)-)----------------| || p+ a n- 2 (V - nb) = nRT | |--------V-------------------| ------------------------------

Dies ist die sogenannte Van-der-Waals-Gleichung oder auch die Zustandsgleichung realer Gase. Der Term a² wird häufig als Binnendruck bezeichnet. nb ist das sogenannte Kovolumen. Mit a = b = 0 erhalten wir wieder:

|----------| p .V = nRT | ------------

Also folgt hier die Zustandsgleichung idealer Gase.

Innere Energie U des realen Gases:

dU = d(kinetische Energie+ potentielle Energie) = 3 nR dT+Binnendruck.dV = 3nR dT +a (n-)2 dV 2 2 V

Wir integrieren diesen Ausdruck:

|------------------------| | 3 n2 | U-=--2nRT---a-V-=-U-(T,-V)-

Die innere Energie ist somit eine Funktion der Temperatur und des Volumens. Mit a = 0 folgt natürlich wieder die innere Energie des idealen Gases:

U = 3nRT 2

[next] [front] [up]