10.2 Phasenumwandlungen

Wir veranschaulichen diese Funktion graphisch:

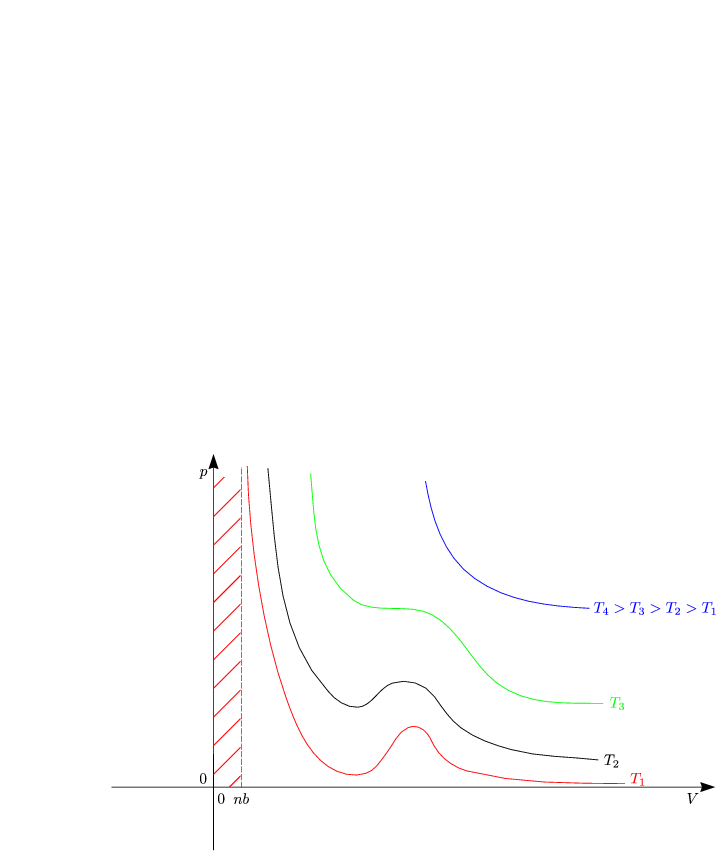
Für große Temperaturen sind Binnendruck und Kovolumen vernachlässigbar und es gilt wieder pV = nRT. Für kleine Temperaturen gibt es Bereiche mit > 0.

Beweis:

• < 0 (Volumenreduktion dV (Fluktuation))

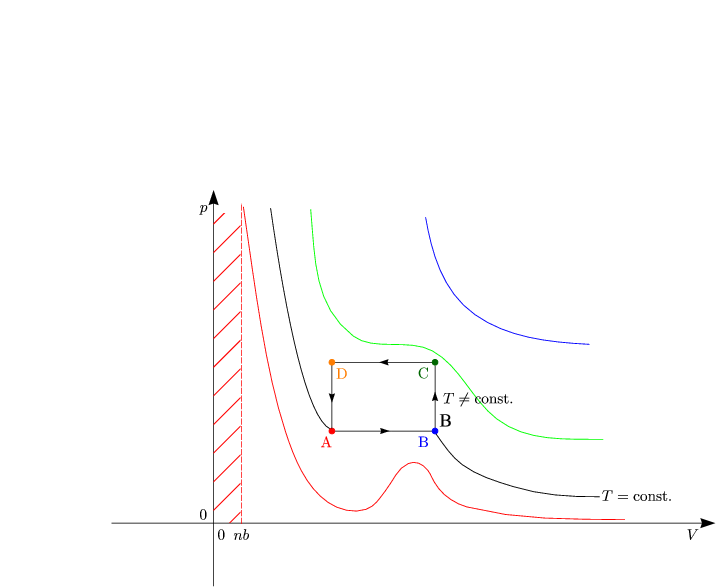
  Der Druck p steigt. Die Kraft auf den Stempel sei konstant. Das Volumen sinkt weiter.

• > 0 (Volumenreduktion dV )

  Der Druck p sinkt. Die Kraft auf den Stempel sei wieder konstant. Das Volumen sinkt somit weiter, weshalb es sich um ein instabiles Verhalten handelt. Dauerhaft kann somit ein Zustand in diesem Bereich nicht auftreten, vorübergehend aber schon.

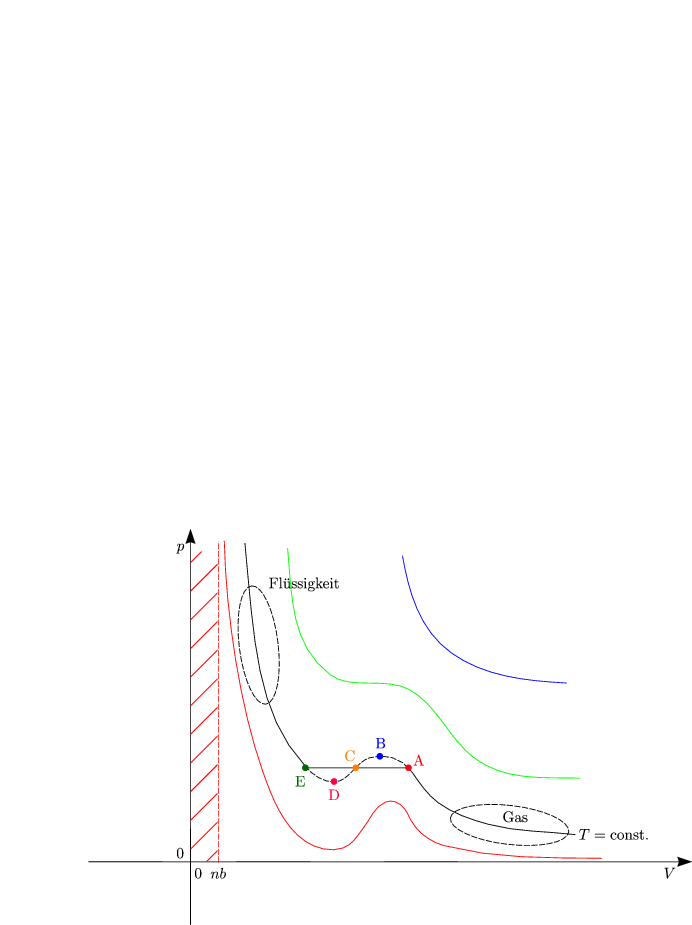
Die Idee ist nun, einen Übergang mit = 0 zu konstruieren. Die Maxwell-Konstruktion beschreibt dabei, daß die Fläche EDC genauso groß sein muß wie die Fläche CBA.

Beweis:

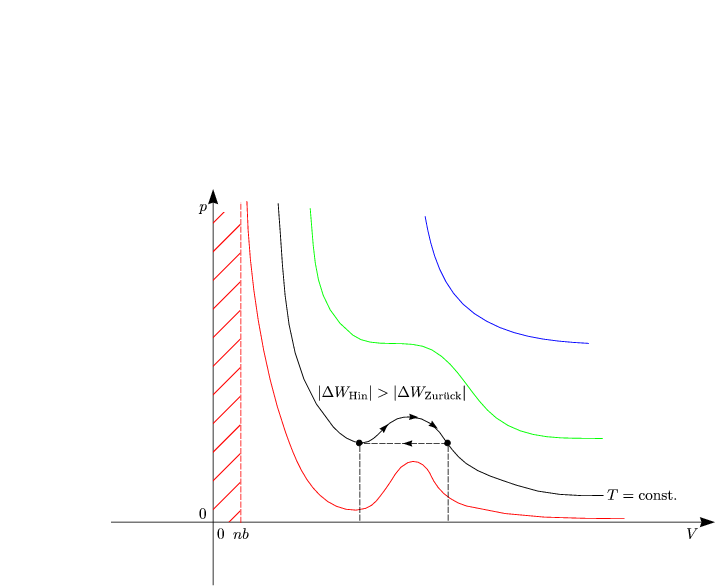
Wir wählen eine andere Horizontale als die Maxwell-Konstruktion es vorschreibt. Wir gehen von E nach A über DCB. Das Gas leistet also die mechanische Arbeit W_Hin. Gehen wir zurück nach E über die Horizontale, so stecken wir weniger mechanische Arbeit W_Zuruck in das Gas hinein als bei der Kompression. Wir sind nun wieder am Anfangszustand angekommen, aber es wurde Arbeit geleistet. Dies entspricht nun dem 1.Hauptsatz.

1. Dieser Punkt entspricht einem übersättigtem Dampf (Kompression und keine Kondensation).
2. Dabei handelt es sich um einen Siedeverzug (Druckabsenkung und keine Keime)

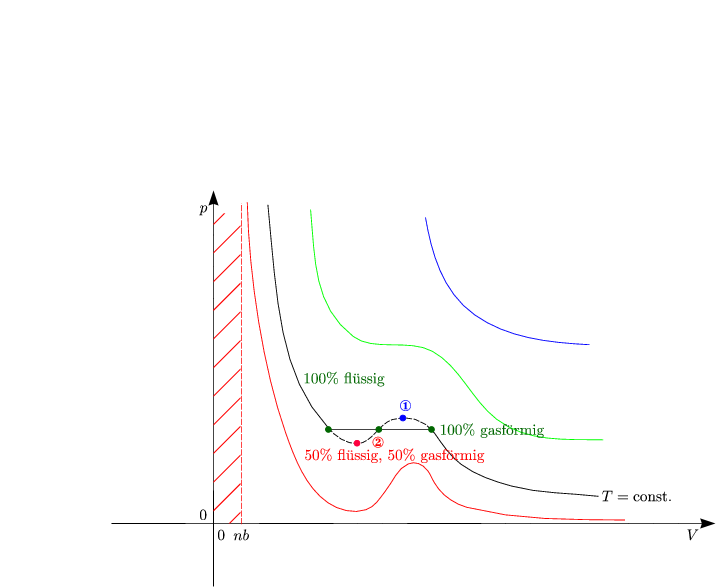
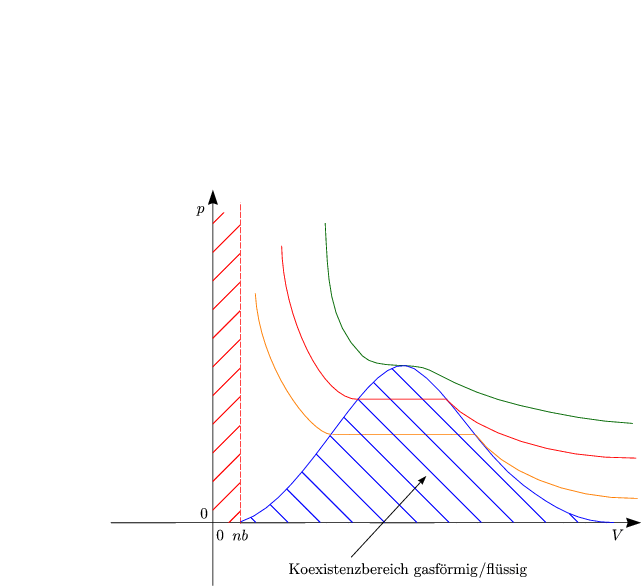
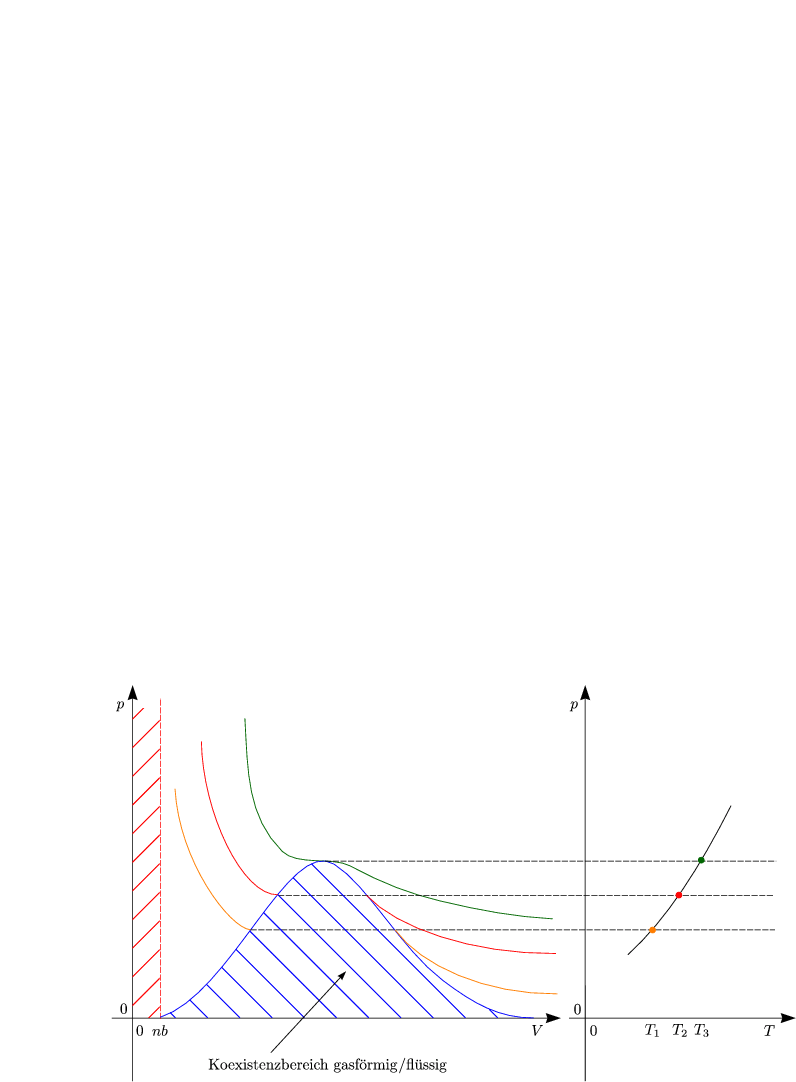
Der Punkt A entspricht einer flüssigen, der Punkt B einer gasförmigen Phase.

• A B: Wir beobachten einen Phasenübergang.
• B C: Das Volumen V sei konstant, wir erhöhen die Temperatur T.
• C D: Der Druck bleibe konstant, wir führen eine Kompression durch.
• D A: Hier sei wieder das Volumen konstant, wobei wir die Temperatur T aber senken.

Auf dem Weg BCDA beobachten wir keinen Phasenübergang. Nur im Koexistenzbereich kann man die Umwandlung aufgrund der unterschiedlichen Brechungsindizes der flüssigen und gasförmigen Phase sehen.

Dampfdruckkurve:

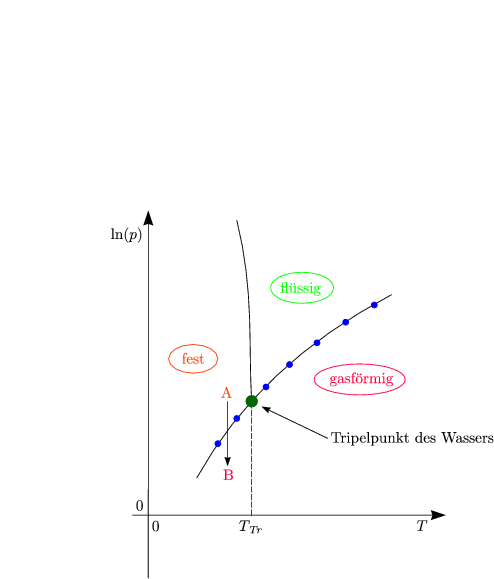
Wir betrachten beispielsweise Wasser (H₂O):

• Für T < T_Tr gibt es keine flüssige Phase mehr! Wenn man p bei T = const. senkt (A B), so gibt es einen Phasenübergang fest/gasförmig (Sublimation).
• Für T > T_Tr kann man bei p = const. einen Phasenübergang flüssig gasförmig hervorrufen. Dieser ist mit einem Sprung in der Entropie verknüpft. Somit macht auch die Wärme Q = T dS einen Sprung, den man auch als latente Wärme bezeichnet. Dies entspricht einem Phasenübergang 1.Ordnung.

  Zur Erinnerung:

  Es ist die Rede von einem idealen Gas mit p = const. (Kapitel 3.1).

  

  

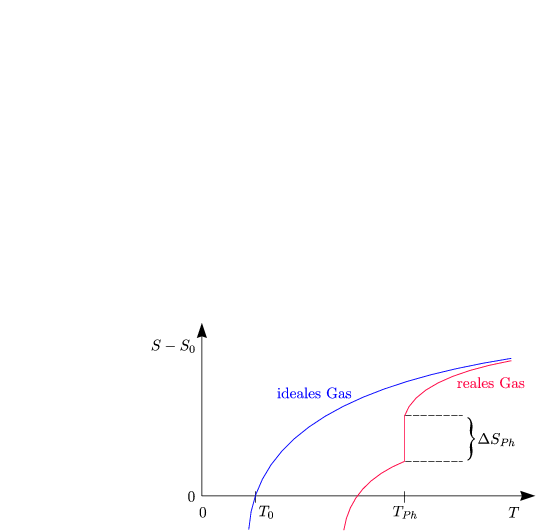
  Die latente Wärme ist: