11.3 Expansion realer Gase

11.3.1 Joule-Thomson-Effekt

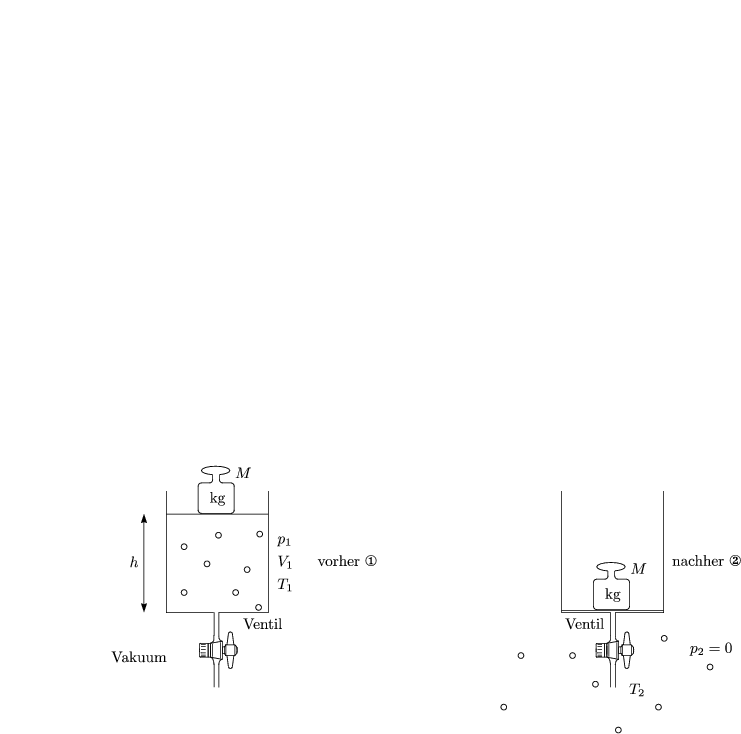
Wir betrachten die irreversible adiabatische Expansion realer Gase.

Die Enthalpie bleibt bei diesem Vorgang konstant:

Die innere Energie U des Gases ist somit nicht erhalten, aber die Enthalpie H = U + pV ist erhalten. Die Enthalpie des realen Gases lautet (Kapitel 5.1):

Außerdem benötigen wir die Zustandsgleichung realer Gase:

Wir lösen nach p auf:

Damit drücken wir die Enthalpie durch T und V aus:

Eigentlich gilt T = T(p,S) und V = V (p,S). Durch Bildung des totalen Differentials ergibt sich:

Wir lösen nach dT auf:

Einsetzen ergibt:

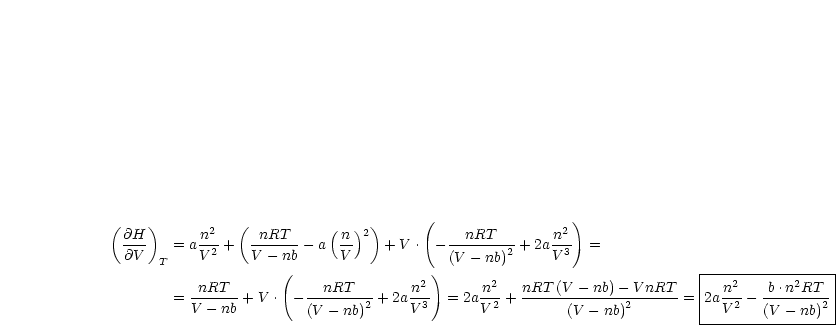(11.3)

Damit resultiert dann für den Bruch:

Der Zähler kann negativ werden für T < T_i. T_i ist die sogenannte Inversionstemperatur. Für T_i ergibt sich:

Da nb « V , ergibt sich schließlich:

Unterhalb der Inversionstemperatur T_i kühlt sich das reale Gas ab, oberhalb erwärmt es sich. Diesen Effekt, den Joule-Thomson-Effekt nutzt man zur Verflüssigung von Gasen. Für ideale Gase folgt:

Damit ist also dT = 0, d.h. die Temperatur des idealen Gases bleibt unverändert.

Beispiele: