12.2 Diffusion

[prev] [prev-tail] [tail] [up]

12.2 Diffusion

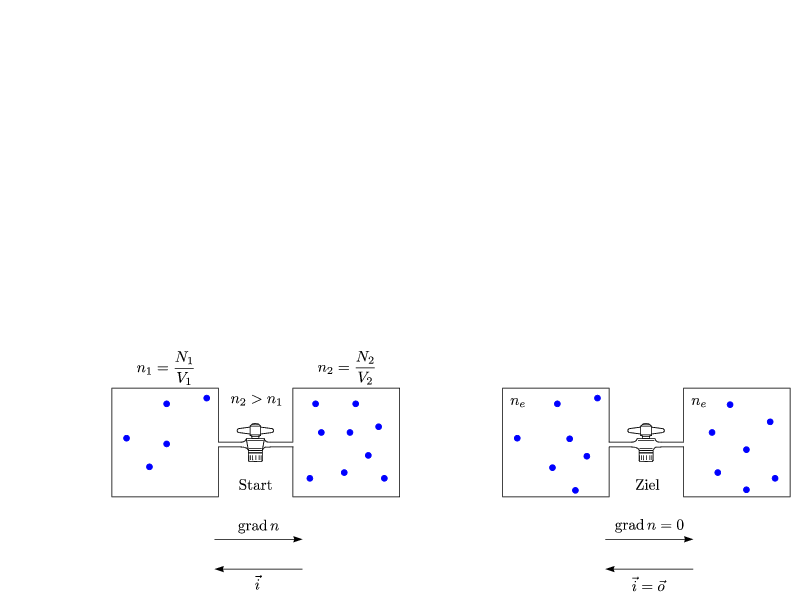
Wovon hängt ab?

Wir verwenden den Ansatz:

--------------- | | -i =--D-.gradn- 1.Ficksches-Gesetz-

/\ m2 D = Diffusionskoeffizient,[D] = -s-

D ist wieder materialspezifisch und kann außerdem von der Teilchenzahl abhängen:

D = D(n)

Durch Einsetzen folgt:

div i+ @u-= 0 @t

div(- D .grad n)+ @u-= 0 @t

Mit DD(n) folgt hieraus die sogenannte Diffusionsgleichung:

|-------------| /_\ n - 1-@u-= 0| 2.Ficksches Gesetz ------D-@t-----

Dieses Gesetz gilt nicht nur für Gase. Au0erdem ist sie mathematisch völlig äquivalent zur Wärmeleitungsgleichung.

Beispiel (Wärmeleitungsgleichung):

/_\ T - ~c@T-= 0 k@t

Wir interessieren uns nur für die stationäre Lösung:

@T @t-= 0 ==> DT = 0

T(x) ist dann eine Gerade.

Beispiel (Diffusionsgleichung in 2D):

Es sei die Anfangsverteilung bei t = 0 gegeben:

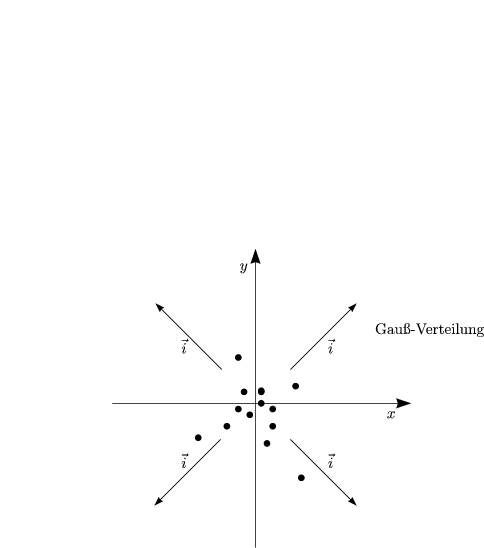
Mit Polarkoordinaten folgt dann:

V~ ------- r = x2 + y2

|---------------(--)-| | - rs0 2| -n(r,t-=-0) =-n0e-----

Die Lösung lautet dann, wie man durch nachrechnen überprüfen sollte:

-1@n- /_\ n - D @t = 0

|-------------------------------------------| | ( s )2 -r- 2 | n(r,t) = --0- n0e-(s(t)) mit s2(t) = s20 + 4Dt ---------s(t)--------------------------------

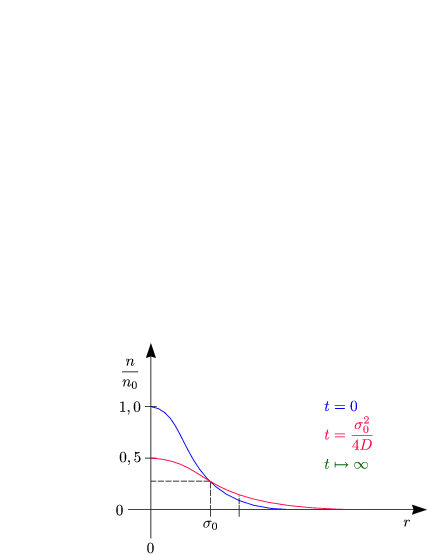
Bei der Diffusion ist der Fall:

|--------------------------| |Breite der Verteilung ~ s ~ V~ t ----------------------------

Zum Vergleich gilt für den freien Flug (ballistisch):

Breite-der Verteilung ~-t -----------------------

[prev] [prev-tail] [front] [up]