


Wir machen folgenden Ansatz:
Einsetzen ergibt:
Dies ist genau die Definition eines Rechtssystems.
Felder haben ausschließlich Tangentialkomponenten.
Wegen ![]() =
= ![]() mit B =
mit B = ![]() 0H:
0H:
Dieses Resultat wird nun in die obige Bestimmungsgleichung eingesetzt:

Dies ist nun der Feld-Reflexionskoeffizient. Weiterhin erhält man die Fresnelsche Gleichung:
t ist der sogenannte Feld-Transmissionskoeffizient.

Wir machen eine Tabelle:
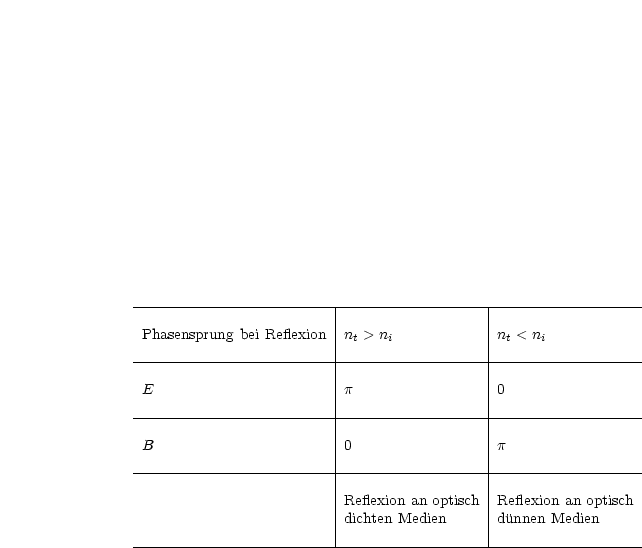
Somit folgen die Koeffizienten für die Intensität I:
Es gilt außerdem:

Mit |![]() t| =
t| = ![]() =
= ![]() nt =
nt = ![]()
![]() = |
= |![]() i|
i|![]() folgt das Snellius-Brechungsgesetz:
folgt das Snellius-Brechungsgesetz:


Der Grenzwinkel der Totalreflexion ![]() i =
i = ![]() G entsteht bei der Reflexion an optisch
dünneren Medien.
G entsteht bei der Reflexion an optisch
dünneren Medien.
H2O mit n = 1,5 hat einen Grenzwinkel ![]() G von etwa 42o.
G von etwa 42o.
Wie groß sind r, t, R, T? Im Gegensatz zum senkrechten Einfall, gibt es ein
Problem: v, t, R, T hängen von Richtung von ![]() in Bezug auf die Einfallsebene
ab!
in Bezug auf die Einfallsebene
ab!


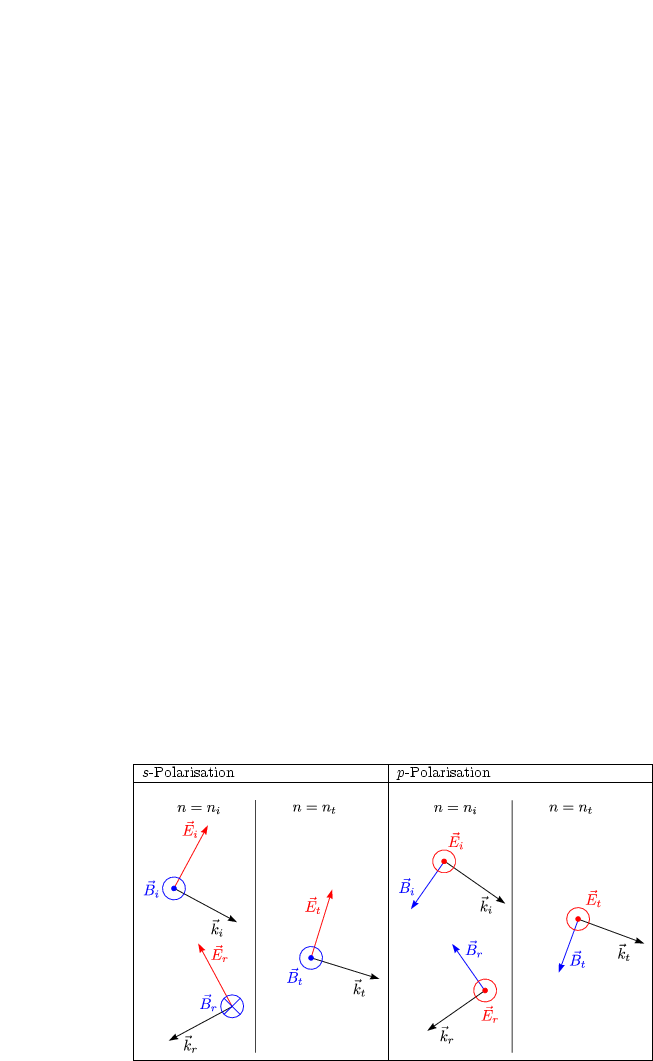

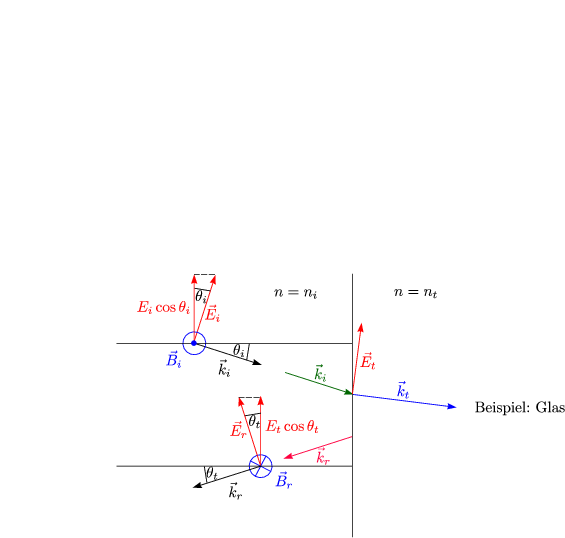

Unser Vorgehen ist analog zu Kapitel 3.1.1. Die zu verwendende Stetigkeitsbedingung natürlich bezogen auf die Parallelkomponenten der Feldvektoren lautet:
Außerdem gilt analog zu vorher:
Dieses Resultat wird nun wieder oben eingesetzt:
Damit folgt:
Und schließlich gilt:
Analog erhält man die restlichen Beziehungen:
![]() t ergibt sich aus dem Brechungsgesetz von Snellius. Es handelt sich um die Fresnelschen
Gleichungen für rs, rp, ts und tp. In der p-Polarisation gibt es ein
t ergibt sich aus dem Brechungsgesetz von Snellius. Es handelt sich um die Fresnelschen
Gleichungen für rs, rp, ts und tp. In der p-Polarisation gibt es ein ![]() i mit R = 0.
Diesen Winkel
i mit R = 0.
Diesen Winkel ![]() i nennt man Brewster-Winkel.
i nennt man Brewster-Winkel.
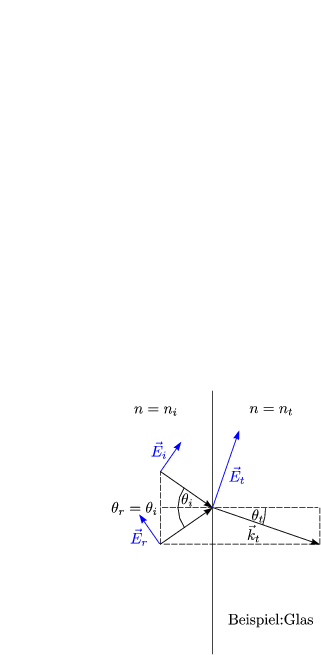

Es gilt ja folgende Maxwellsche Gleichung, welche ![]() und
und ![]() verknüpft:
verknüpft:
Wir verwenden folgende Ansätze für ![]() und
und ![]() :
:
Damit resultiert dann durch Einsetzen in obige Gleichung:
Aufgrund des Vektorproduktes gilt also ![]()
![]()
![]() . Damit wird keine Welle abgestrahlt
mit
. Damit wird keine Welle abgestrahlt
mit ![]() ||
||![]() .
.

Mit dem Brechungsgesetz folgt:
Daraus folgt:
Dies ist der Brewster-Winkel.
Es sei eine System gegeben mit ni = 1 und nt = 1,5. Dann folgt damit der Brewster-Winkel zu:
Für ein anderes System gilt ni = 1,5 und nt = 1. Auch hier folgt: