2.2 Dielektrische Schichtsysteme

Kann man die Reflexion von Licht an Oberflächen verstärken oder abschwächen?

2.2.1 /4-Antireflexschicht

Es gibt eine destruktive Interferenz der Partialwellen 1 und 2, falls der Phasenunterschied „Hin-und-Zurück“= 180^o ist, d.h.:

Deshalb heißt die Schicht /4-Schicht. ist natürlich die Wellenlänge im Medium mit Brechzahl n. Wir groß muß n₁ sein für den optischen Effekt? Die Partialwellen 1 und 2 sind nach dem Betrage gleich groß. Damit muß also auch gelten:

Hier fallen viele Koeffizienten weg, wobei nun folgt:

Es handelt sich also um das geometrische Mittel.

Beispiel:Antireflexbeschichtung von Glas/Luft

Man erhält eine Verbesserung, indem man komplexere Schichtsysteme verwendet. Dies wollen wir im folgenden Kapitel betrachten:

2.2.2 Transfermatrixmethode, Spiegel

• Grenzfläche I:

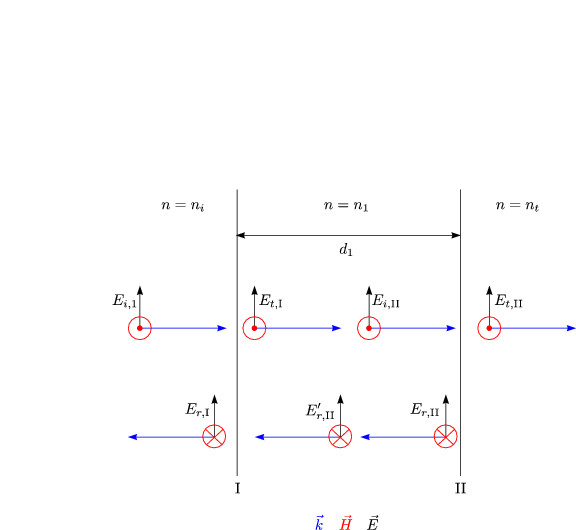
  Wir notieren uns die Stetigkeitsbedingungen der Tangentialkomponenten von und :

  
  

  Oder mit H = E = nE = Z^-1E folgt:

  

  Z ist hierbei die Medien-Impedanz.

  

• Grenzfläche II:
  

Phasenverzögerung:

Dies folgt mit = c₁ = . Die grundlegende Idee bei Mehrschichtsystemen ist nun folgende:

M_I ist die charakteristische Matrix (Transfermatrix). Durch Ausmultiplizieren der ersten Zeile ergibt sich:

(2.1)

Durch Zusammenfassung der Ausdrücke folgt:

(2.2)

Durch Vergleich der linken und rechten Seite der Gleichung resultiert das folgende Gleichungssystem:

• ^. = 1
• cos(k₁d₁) - isin(k₁d₁) = m₁₁ - m₁₂Z₁^-1

Durch Koeffizientenvergleich erhält man aus der zweiten Gleichung:

Durch Einsetzen in die erste Gleichung folgt:

Damit erfüllt die Lösung auch die erste Gleichung, womit wir also die erste Zeile unserer Matrix M kennen. Die zweite Zeile folgt analog und kann als Übung nachgerechnet werden. Damit notieren wir das Endergebnis der Transfermatrix:

Analog zu Einschichtsystemen können nun N Schichten behandelt werden:

Hiermit können r und t „leicht“ bestimmt werden:

Wir dividieren durch E_i,I mit folgendem Resultat:

Somit folgt für r und t durch Auflösen dieses Gleichungssystems:

Diese Gleichungen gelten sowohl für den Feld-Reflexionskoeffizient r = als auch für den Feld-Transmissionskoeffizient t = .

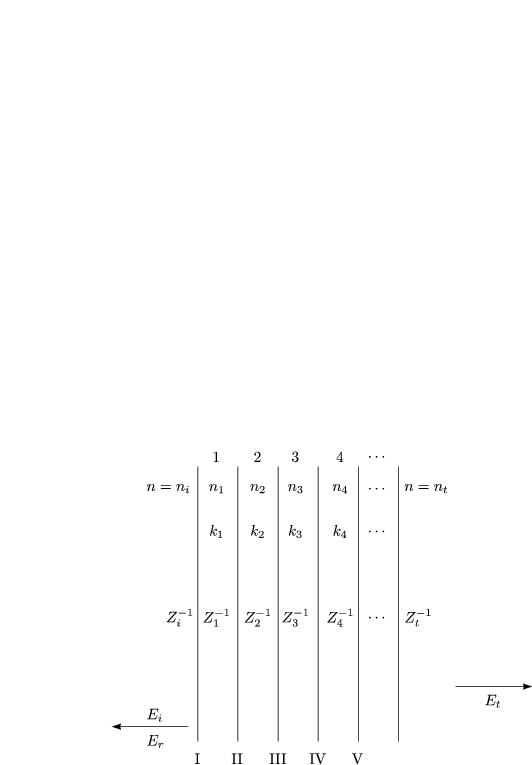
Oder abgekürzt:

Folgende Substanzen werden bei der Herstellung verwendet:

Anwendung:

Spiegel für Laser, Filter, ...

2.2.3 Fabri-Perot-Interferometer

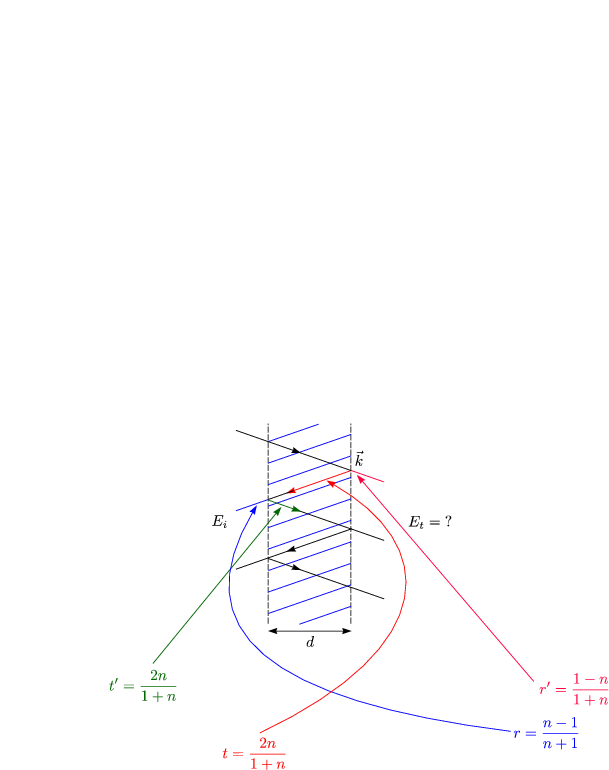
Dies folgt mit der Phasenverschiebung = k ^.d^. 2 = k₀ ^.n^.d^. 2. Die Formel können wir mittels der geometrischen Reihe vereinfachen:

Durch Einsetzen ergibt sich:

Mit den Intensität folgt:

Und mit tt' + r² = 1, tt' = 1 - r² ergibt sich:

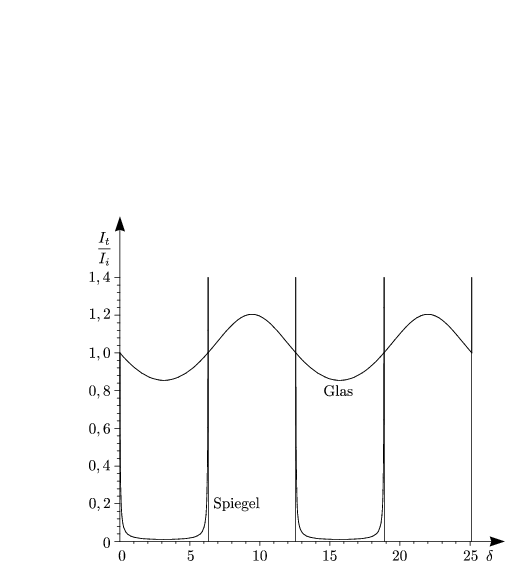
Wir haben hier die sogenannte Airy-Formel hergeleitet mit dem Finesse-Faktor F und r:

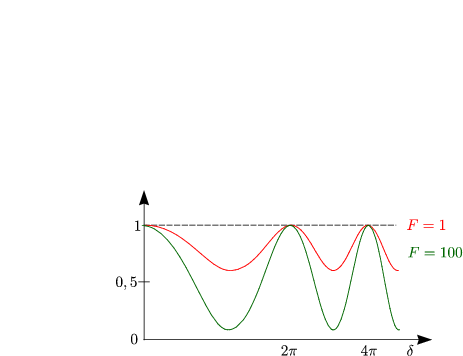
Maxima findet man bei:

Beispiel:

• Glas mit n = 1,5:

  Außerdem folgt der Finesse-Faktor:

  

• Spiegel mit r = 0,9:

2.2.4 Photonische Kristalle

• Eindimensionaler Fall:

  

• Zweidimensionaler Fall:

  

• Dreidimensionaler Fall:

  

Definition:

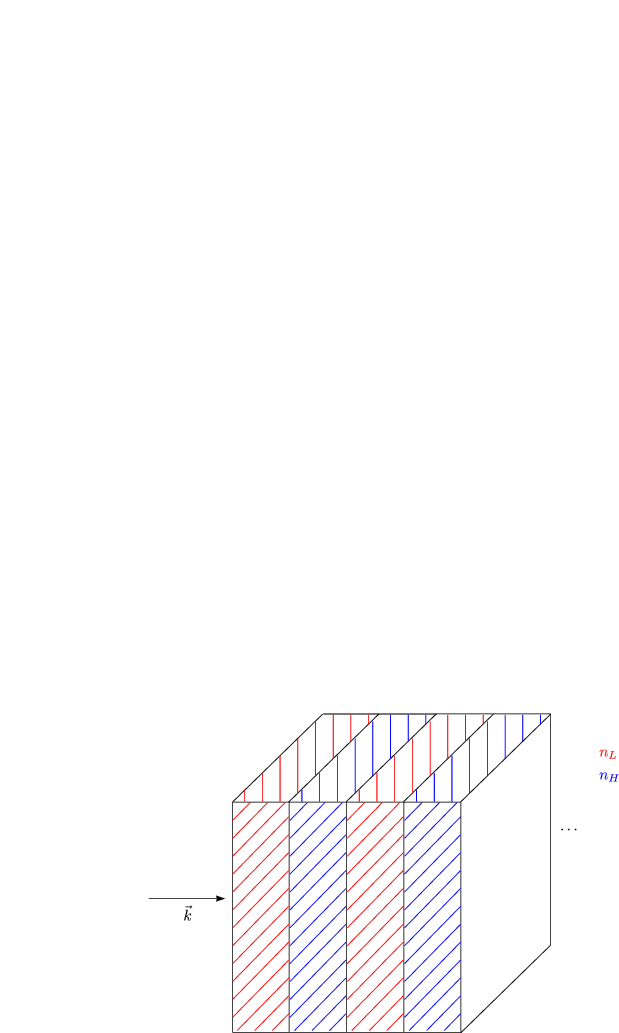
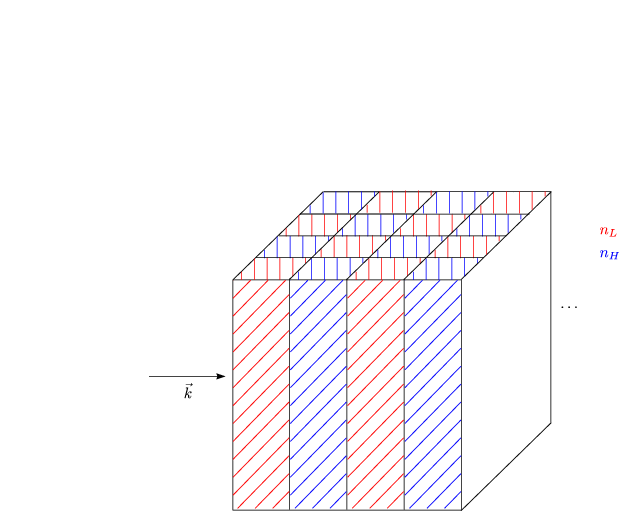
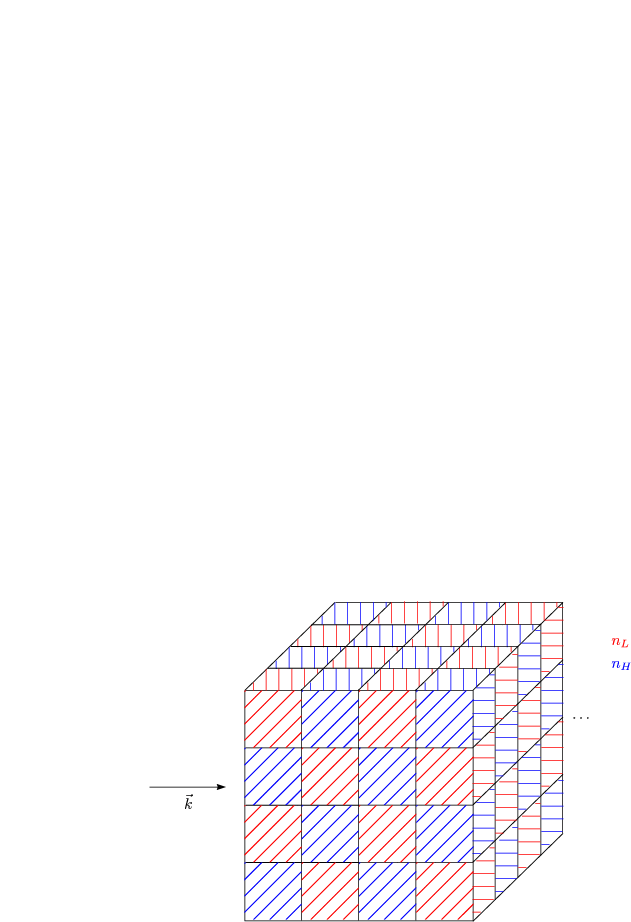
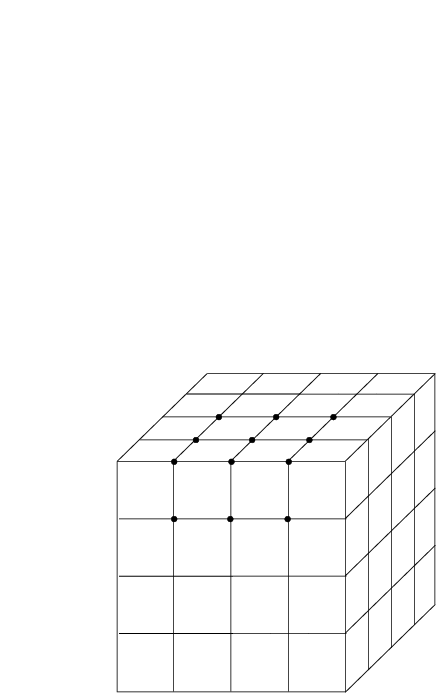
Die Punkte stellen Atome oder Gruppen aus Atomen dar.

Brechzahl:

a wird als Gitterkonstante bezeichnet. Es gilt:

Es handelt sich somit um eine „Gittertranslationsinvarianz“, wobei des weiteren noch gilt:

Wir machen einen Ansatz:

Dies ist die sogenannte Bloch-Funktion. u_k ist eine gitterperiodische Funktion, für die gilt:

Hieraus folgt nun das Bloch-Theorem:

(x) ist nicht gitterperiodisch. Ohne Beweis ergibt sich, daß dieser Ansatz die Wellengleichung löst für bestimmte u_k(x) und zugleich auch allgemein gültig ist. Wir betrachte nun folgende Transformation:

Daraus folgt:

Die Idee ist nun, daß man sich auf die Darstellung eines Intervalls der Breite beschränkt (Brillouin-Zone).

Beispiel:

2.2.5 Brillouin-Zone

Beispiel:

Weiteres Beispiel:

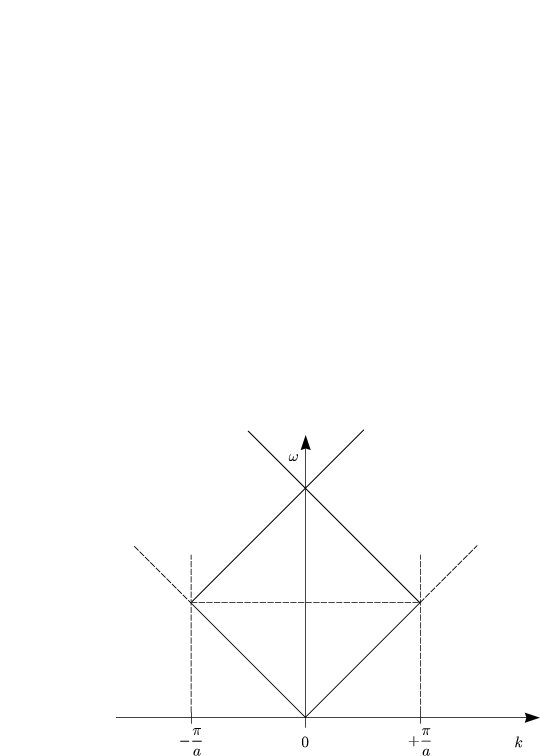
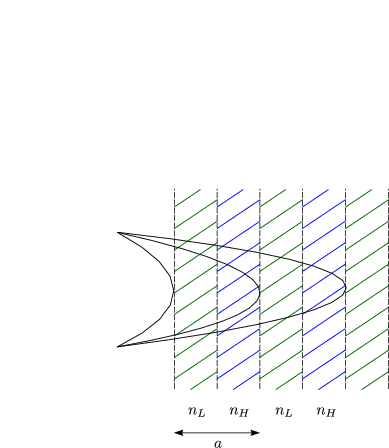
Wir schauen uns nun zwei Materialien mit verschiedenen Brechzahlen an:

Wir betrachten speziell k = ±, was ein Part der Brillouin-Zone darstellt.

Die Partialwellen überlagern sich somit alle konstruktiv. Man erhält somit eine starke Reflexion. Angenommen, wir haben eine ebene Welle mit dem Wellenvektor k. Die reflektierten Wellen, die von rechts nach links zurücklaufen, besitzen dann den Wellenvektor -k. Es findet dann eine Interferenz statt, wobei eine stehende Welle im Material entsteht. Dabei gibt es zwei Möglichkeiten (schematisch):

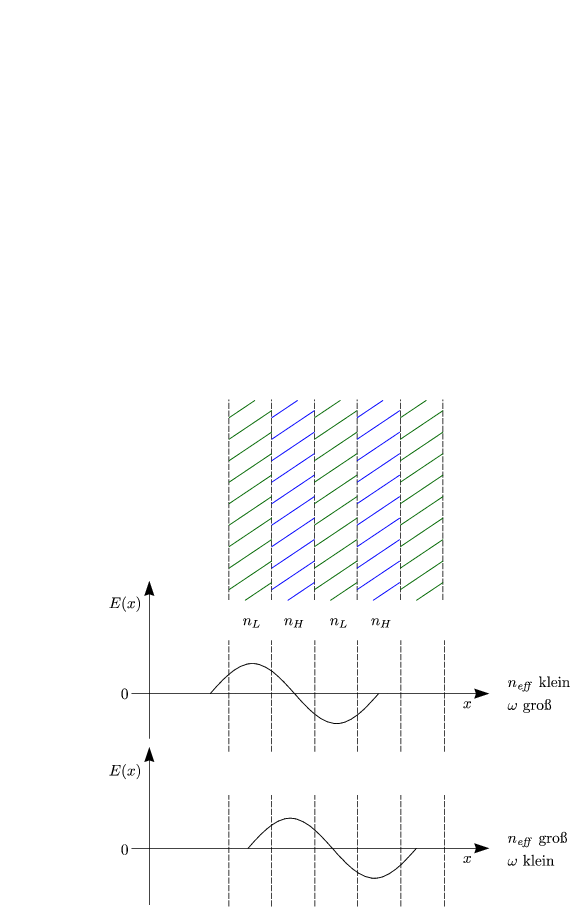
Bei k = ± gibt es somit zwei verschiedene . Bei k ± gibt es auch reflektierte Partialwellen; sie mitteln sich aber größtenteils weg. Daher entstehen keine stehenden Wellen.

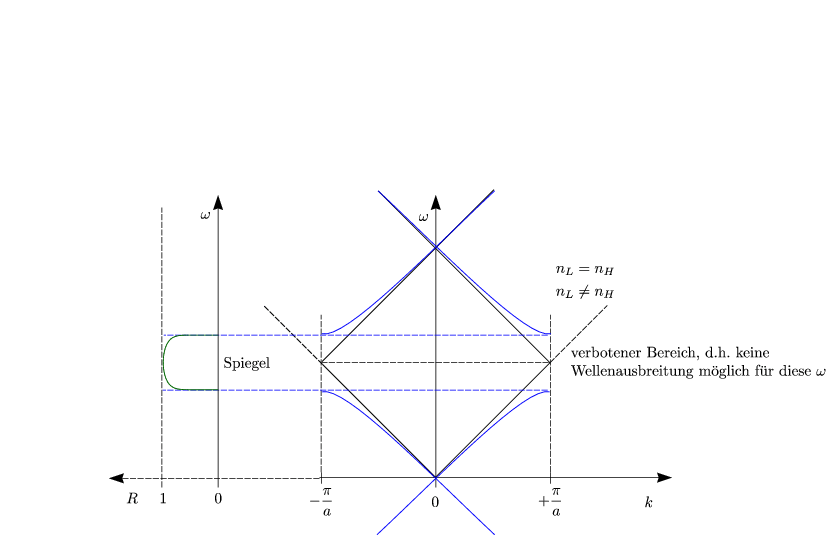
Wir sehen hier die Bandstruktur von Licht (Photonen) (siehe Festkörperphysik)

Anwendungsbeispiel:

Ich kann mir beispielsweise folgende Geometrie überlegen, die für einen bestimmten Frequenzbereich eine Bandlücke aufweist:

Somit sind Wellenleiter auf Mikroebene realisierbar.

2.2.6 Wellenleiter

Beispiele:

• Glasfaser

  

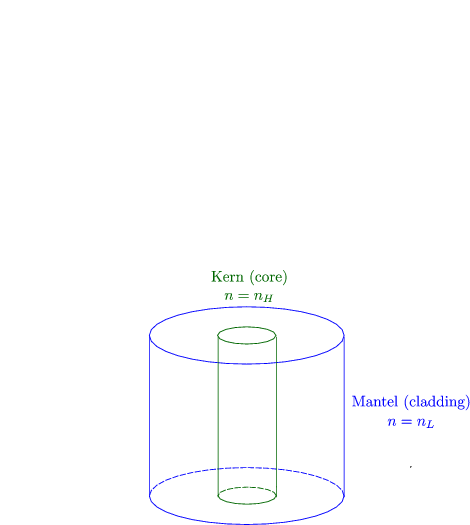
  Typisch sind folgende Brechzahlen:

  
  

• Rippenwellenleiter

  

• Planarer symmetrischer Wellenleiter

  

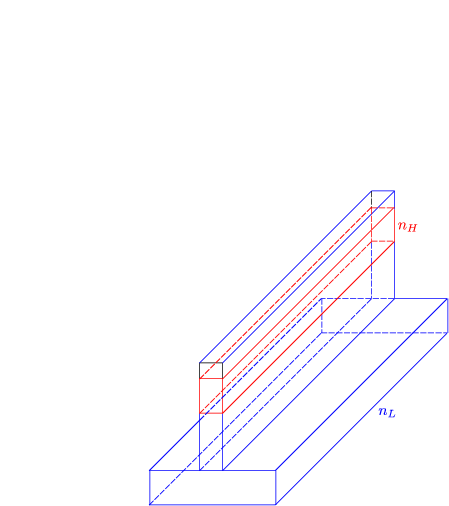
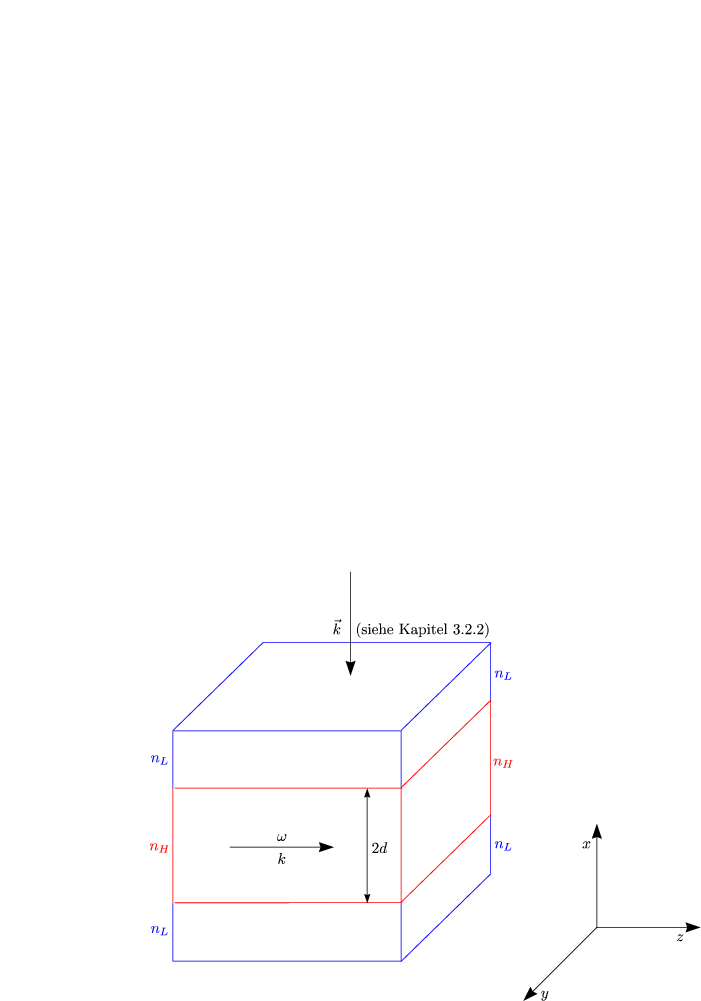
  Es gibt zwei unterschiedliche Polarisationen:

  • Transversal magnetischer Fall:

    

  • Transversal elektrischer Fall:

    

  Wir betrachten hier nur die TE-Polarisation. Die Wellengleichungen lauten:

  
  

  Wir verwenden den Ansatz:

  

  Dieser Ansatz wird eingesetzt, woraus folgt:

  

  ² ist innerhalb eines Mediums konstant, da n = const.. ² kann aber sowohl größer als auch kleiner als 0 sein.

  Teillösungen:

  • 1.Fall: ² = _H² > 0; d.h. große Brechzahl bei festem

    Wir wählen hier den Ansatz folgendermaßen, da es sich um eine Schwingungsgleichung handelt:

    

    Wenn wir diesen Ansatz einsetzen, stellen wir fest, daß er die Wellengleichung löst.

  • 2.Fall: ² = -_L² < 0; d.h. kleine Brechzahl bei festem

    Wir wählen den Ansatz:

    

    Als Randbedingungen für die Lösung erwarten wir:

    • _y bei x = ±d sei stetig.
    • _y (x±) = 0
    • Ableitungen von _y bei x = ±d sei stetig.

    

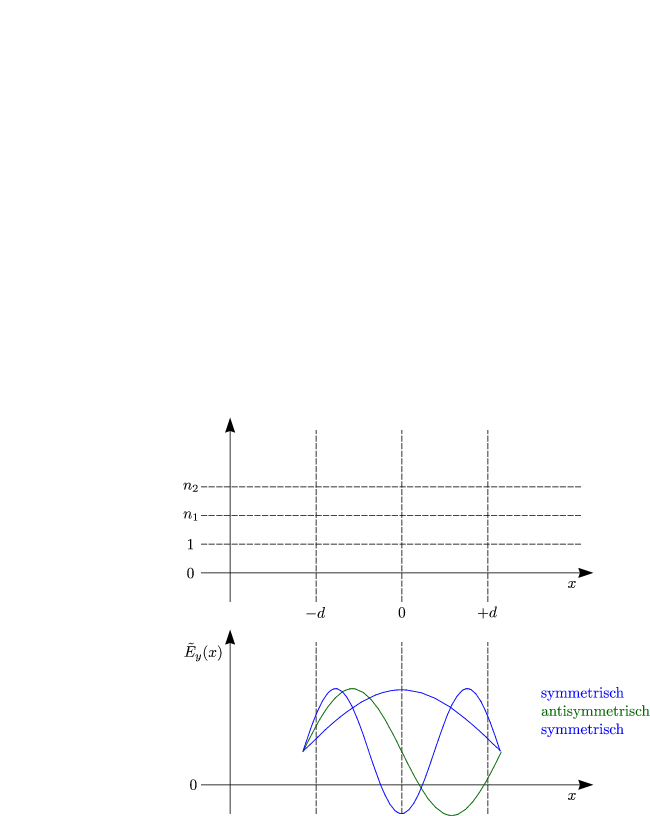
    Betrachte hier nur symmetrische Lösungen, d.h. A = 0 (antisymmetrisch analog). Wir untersuchen die Stetigkeit von _y(x) bei x = ±d.

    • x = +d:

    • x = -d:

    Für die Stetigkeit bei x = ±d folgt:

    • x = ±d:

    • x = -d:

    Die ersten beide Terme werden addiert, die zweiten subtrahiert, woraus sich dann ergibt:

    
    

    Die beiden Gleichungen werden durcheinander dividiert:

    

    Der Term _H tan(_Hd) läßt sich analytisch nicht berechnen. Es handelt sich um eine transzendente Gleichung zur Bestimmung von k_z. Zur Erinnerung notieren wir uns nochmals die Gleichungen vom Anfang:

    
    

    Die Idee ist es nun, _L durch _H auszudrücken:

    

    Daraus folgt:

    

Durch Einsetzen folgt:

Es handelt sich hierbei um eine transzendente Gleichung, welche analytisch nicht gelöst werden kann. Infolgedessen lösen wir das Problem graphisch:

• Es existiert immer mindestens eine Lösung, wenn n_H > n_L ist.
• Es existiert keine Lösung für n_H < n_L.
• Es existieren endlich viele Lösungen abhängig von (n_H² - n_L²)d².

Beispiel:

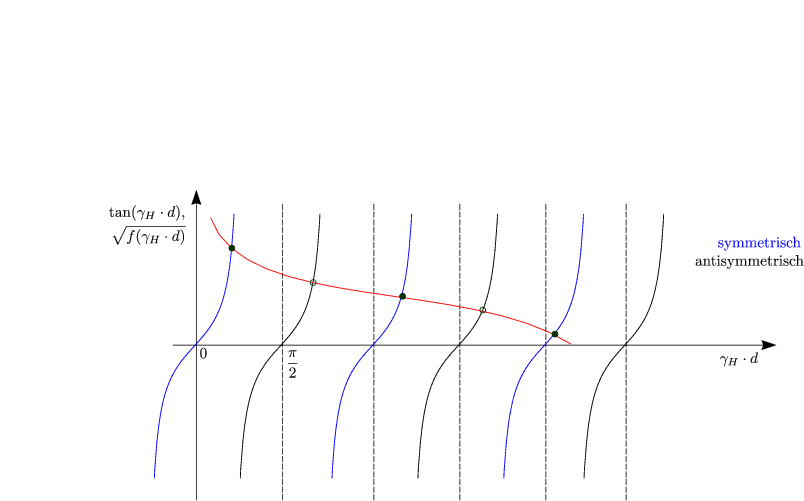
Dies ist der Fall bei einem „dünnen Wellenleiter“. Es existiert nur eine Lösung.

Anmerkung:

Bei Wellenführung in zwei bzw. drei Dimensionen existiert hingegen nicht immer eine propagierende Lösung. Wir kommen auf diesen Sachverhalt unter dem Stichwort evaneszente Wellen zurück (Kapitel 4). Die unterschiedlichen Lösungen werden oft auch als Moden bezeichnet.