Im Kapitel 2.3 hatten wir bereits gesehen, daß es Materialien gibt bei denen die
Brechzahl von der Richtung von ![]() (Polarisation) abhängt. Die Komponenten von
(Polarisation) abhängt. Die Komponenten von ![]() laufen also im allgemeinen mit unterschiedlichen Phasengeschwindigkeit
(Anisotropie).
laufen also im allgemeinen mit unterschiedlichen Phasengeschwindigkeit
(Anisotropie).
Im Kalkspat (CaCO3) gibt es eine ausgezeichnete kristallographische Achse, die
![]() -Achse.
-Achse.


Für ![]() =
= ![]() oder
oder ![]() =
= ![]() bleibt alles wie in Kapitel 3.1.1. Interessant ist
bleibt alles wie in Kapitel 3.1.1. Interessant ist
![]() = E0
= E0![]() ei
ei![]() vor dem Plättchen. Im Vakuum gilt:
vor dem Plättchen. Im Vakuum gilt:
Reflexionen seien hier natürlich vernachlässigt. Diese können sowieso durch Antireflexbeschichtungen verhindert werden.


Mit ![]() =
= ![]() und
und ![]() =
= ![]() folgt:
folgt:
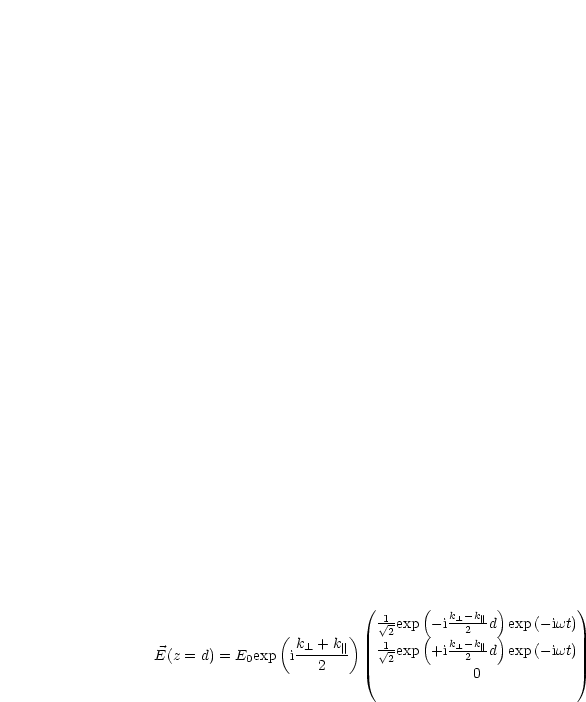
Dies gilt mit ![]() :=
:= ![]() . d = k0
. d = k0![]()
![]() .
. ![]() ist Phasenverschiebung zwischen
x- und y-Komponente.
ist Phasenverschiebung zwischen
x- und y-Komponente.
Betrachte den Realteil von ![]() :
:
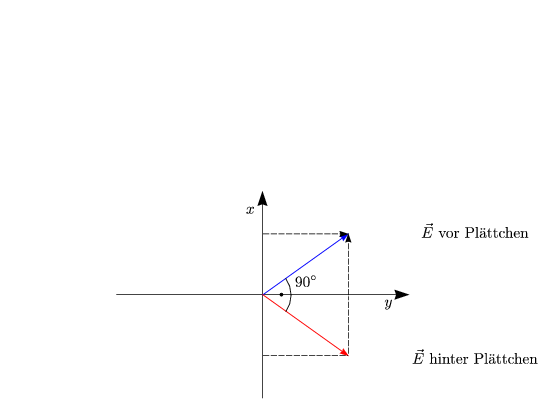
Die lineare Polarisation wird um 90o gedreht.
Wir betrachten wieder den Realteil von ![]() : Mit
: Mit ![]() =
= ![]() . d +
. d + ![]()
![]() uninteressant
uninteressant
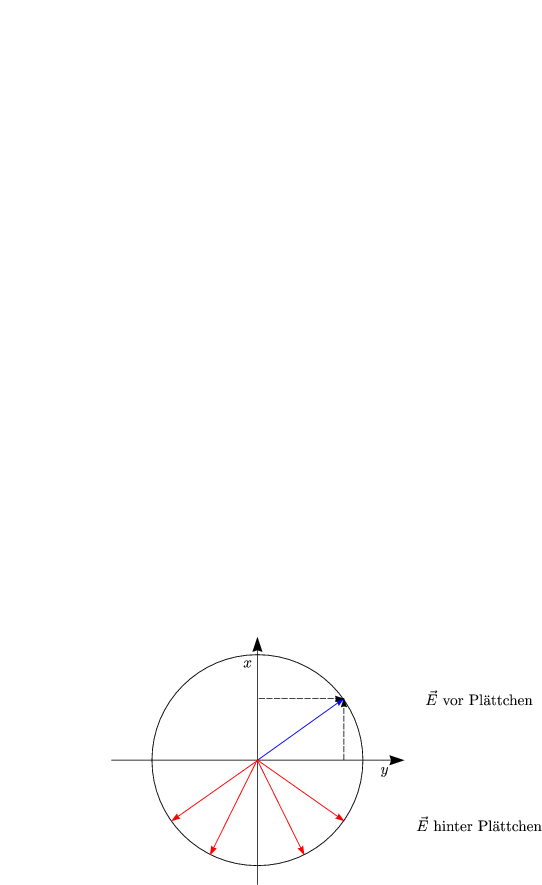
Lineare Polarisation wird zu zirkularer Polarisation.
![]() i hat nur eine Komponente senkrecht zu
i hat nur eine Komponente senkrecht zu ![]() .
.
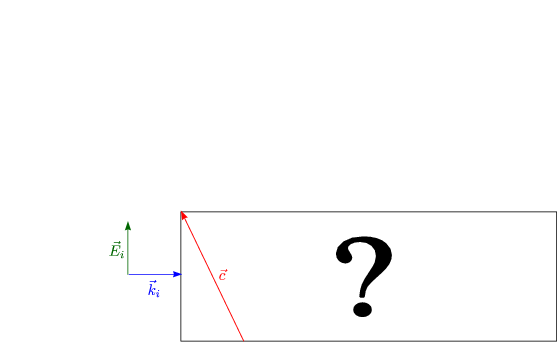
![]() i hat Komponenten parallel und senkrecht zu
i hat Komponenten parallel und senkrecht zu ![]() . Wir stehen
. Wir stehen ![]() ,
, ![]() ,
, ![]() und
und ![]() im
doppelbrechenden Material zueinander? In Kapitel 2.5 hatten wir gesehen, daß
gilt:
im
doppelbrechenden Material zueinander? In Kapitel 2.5 hatten wir gesehen, daß
gilt:
![]() ist der Dielektrizitätstensor (3X3-Matrix). Im allgemeinen ist die Richtung von
ist der Dielektrizitätstensor (3X3-Matrix). Im allgemeinen ist die Richtung von ![]() nicht identisch mit der Richtung von
nicht identisch mit der Richtung von ![]() ! Aus div
! Aus div![]() = 0 folgt mit dem Ansatz
= 0 folgt mit dem Ansatz
![]() =
= ![]() 0e-i
0e-i![]() :
:
Das bedeutet, daß ![]() senkrecht zu
senkrecht zu ![]() steht. Im allgemeinen steht aber
steht. Im allgemeinen steht aber ![]() nicht senkrecht zu
nicht senkrecht zu ![]() ! Aus div
! Aus div![]() = 0 folgt mit dem Ansatz
= 0 folgt mit dem Ansatz ![]() =
= ![]() 0ei
0ei![]() folgt:
folgt:
Daraus folgt, daß ![]() senkrecht auf
senkrecht auf ![]() steht. Wegen
steht. Wegen ![]() =
= ![]() ×
×![]() (mit
(mit ![]() =
= ![]() 0
0![]()
![]()
![]() ||
||![]() ) ist im allgemeinen
) ist im allgemeinen ![]() nicht parallel zu
nicht parallel zu ![]() .
. ![]() kann somit nicht mehr als
Ausbreitungsrichtung interpretiert werden. Aber aufgrund der Definition stehen
kann somit nicht mehr als
Ausbreitungsrichtung interpretiert werden. Aber aufgrund der Definition stehen ![]() und
und ![]() senkrecht aufeinander. Also folgt:
senkrecht aufeinander. Also folgt:

Wir fassen unsere Resultate zusammen:


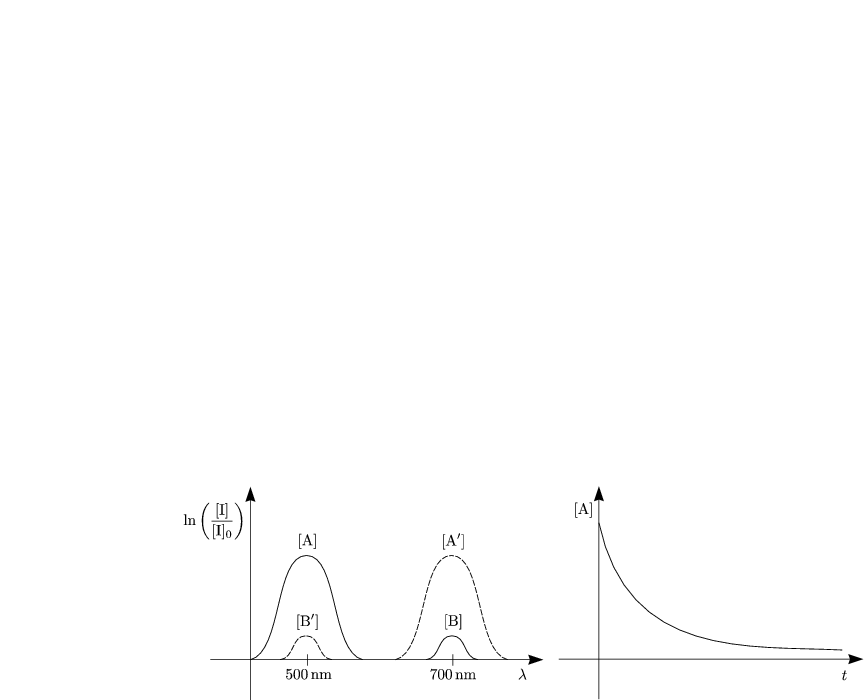
Der Grenzwinkel der Totalreflexion ![]() G folgt aus:
G folgt aus:
Wegen n![]() > n|| beim Kalkspat ergibt sich:
> n|| beim Kalkspat ergibt sich: