Atome bilden gemeinsame Orbitale, welche mit Elektronenpaaren besetzt sind.
Diese müssen dann jedoch umgekehrten Spin (![]()
![]() ) haben. Diese Art der
Bindung wird quantenmechanisch behandelt. Das einfachste Beispiel für eine
Elektronenpaar-Bindung ist das H2-Molekül. Da dieses jedoch aus 4 Teilchen besteht,
kann das Problem nicht mehr analytisch gelöst werden. Betrachtet man das
H2+-Molekülion, so stellt man fest, daß dieses immer noch aus drei Teilchen besteht
und infolgedessen auch nicht analytisch lösbar ist, womit wir Näherungen machen
müssen. Wichtig ist hier die sogenannte Born-Oppenheimer-Näherung (adiabatische
Näherung), nach der mKern » me, womit vKern
) haben. Diese Art der
Bindung wird quantenmechanisch behandelt. Das einfachste Beispiel für eine
Elektronenpaar-Bindung ist das H2-Molekül. Da dieses jedoch aus 4 Teilchen besteht,
kann das Problem nicht mehr analytisch gelöst werden. Betrachtet man das
H2+-Molekülion, so stellt man fest, daß dieses immer noch aus drei Teilchen besteht
und infolgedessen auch nicht analytisch lösbar ist, womit wir Näherungen machen
müssen. Wichtig ist hier die sogenannte Born-Oppenheimer-Näherung (adiabatische
Näherung), nach der mKern » me, womit vKern ![]() 0 ist. Außerdem findet kein
Energieaustausch zwischen Elektronen und Kern statt. Als erstes wollen
wir uns den Hamilton-Operator notieren, welches das System beschreiben
soll:
0 ist. Außerdem findet kein
Energieaustausch zwischen Elektronen und Kern statt. Als erstes wollen
wir uns den Hamilton-Operator notieren, welches das System beschreiben
soll:
Die kinetische Energie wird beschrieben durch:
Außerdem gilt für den Laplace-Operator:
Wir betrachten hierbei das zeitunabhängige Problem. Dazu setzen wir dies in die stationäre Schrödingergleichung ein, woraus wir die Eigenwerte und Eigenfunktionen erhalten. Dies geh jedoch nicht analytisch! Zuerst betrachten wir deshalb H2+ ohne die 2.Zeile des Hamilton-Operators, was jedoch auch nicht analytisch lösbar ist. Wir machen deshalb folgenden Ansatz als Näherungslösung:
Diese Methode nennt man LCAO-Methode (Linear Combination of Atomic
Orbitals). ![]() a und
a und ![]() b sind aus der Betrachtung des Wasserstoffatoms selbst bekannt.
Diese sind außerdem normierbar:
b sind aus der Betrachtung des Wasserstoffatoms selbst bekannt.
Diese sind außerdem normierbar:
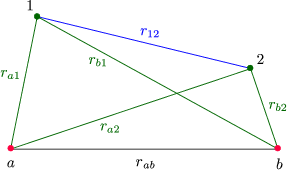
Falls rab sehr groß ist, befindet sich das Elektron entweder bei a oder bei b. Damit folgt für den Grundzustand:
Bei Annäherung gibt es einen schwachen Überlapp. Zu bestimmen sind nun die Konstanten a und b. Dazu setzen wir den obigen Ansatz in die Schrödingergleichung ein und erhalten:
Hierbei gilt dann für die Eigenwerte E:

Mit H und ![]() ergibt sich dann:
ergibt sich dann:
Bei großem rab, folgt aus Haa und Hb die Grundzustandsenergie des Wasserstoffatoms E0 = -13,6eV. In Gegenwart des zweiten Kerns ändert sich die potentielle Energie des ersten Elektrons und außerdem muß die Kern-Kern-Abstoßung berücksichtigt werden:
Man bezeichnet dieses S als Überlappintegral.
![]()
In diesem Falle gilt S![]() 0.
0.

Hier ist S = 0. Außerdem haben wir eine weitere Größe:
Dieses Integral bezeichnet die Wechselwirkungsenergie (Austausch-Energie).
Die Energie befindet sich wegen des Elektrons teilweise in ![]() a und in
a und in ![]() b
(Energieaustausch zwischen den Kernen und nicht zwischen Kern und Elektron!).
Der nächste Schritt, ist a und b zu bestimmen. Man verwendet in diesem
Zusammenhang ein bestimmtes quantenmechanisches Näherungsverfahren, nämlich
das Ritz’sche Variationsprinzip. Grundlage dafür ist, daß für die exakte Lösung
Eexakt < E der Näherungslösung. Um der exakten Lösung möglichst nahe zu
kommen, minimieren wir E bezüglich gewählter Parameter, also in unseren Falle a
und b. Es muß also gelten:
b
(Energieaustausch zwischen den Kernen und nicht zwischen Kern und Elektron!).
Der nächste Schritt, ist a und b zu bestimmen. Man verwendet in diesem
Zusammenhang ein bestimmtes quantenmechanisches Näherungsverfahren, nämlich
das Ritz’sche Variationsprinzip. Grundlage dafür ist, daß für die exakte Lösung
Eexakt < E der Näherungslösung. Um der exakten Lösung möglichst nahe zu
kommen, minimieren wir E bezüglich gewählter Parameter, also in unseren Falle a
und b. Es muß also gelten:
Daraus ergibt sich dann folgendes Gleichungssystem:
Dieses besitzt genau dann nichttriviale Lösungen, wenn die Determinate der Koeffizientenmatrix gleich Null ist:
Für gleiche Kerne ist Haa = Hbb. Also gilt:
Hier gilt außerdem S « 1, weil sonst der Ansatz natürlich auch nicht gut wäre:
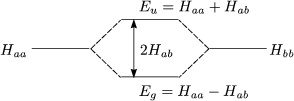
Durch Einsetzen von Eg erhält man a = b und aus Eu folgt a = -b. Durch Normierung erhält man:
Und damit folgt schlußendlich:
Der Unterschied liegt in der Phase der beiden Wellenfunktionen.
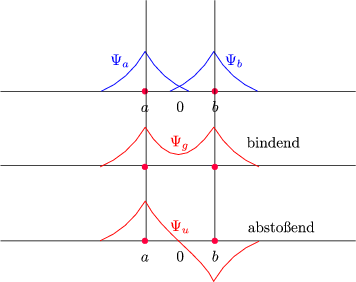
In der Mitte erhalten wir:
Der Faktor 2 ist verantwortlich für den Energiegewinn. Es addieren sich also die Wellenfunktionen anstelle der Dichten!
In der Mitte gilt des weiteren |![]() u|2 = 0.
u|2 = 0.
Für zwei Elektronen muß man sowohl die zweite Zeile des Hamiltonoperators als auch das Pauliprinzip berücksichtigen. Der Spin kommt aber im Hamiltonoperator nicht direkt vor. Die Gesamtwellenfunktion (aller Koordinaten, Ort und Spin) muß antisymmetrisch gegen Vertauschung sein.
![]() Ort setzt sich zusammen aus
Ort setzt sich zusammen aus ![]() g und
g und ![]() a.
a. ![]() Spin besteht aus dem Fall, daß beide
Spins verschieden sind (u:
Spin besteht aus dem Fall, daß beide
Spins verschieden sind (u: ![]()
![]() ) und daß beide Spins gleich sind (g:
) und daß beide Spins gleich sind (g: ![]()
![]() ). Nach dem
Pauliprinzip ist nur
). Nach dem
Pauliprinzip ist nur ![]() g, u oder
g, u oder ![]() u, g kombinierbar.
u, g kombinierbar. ![]() Ort und
Ort und ![]() Spin müssen an
den Hamilton-Operator angepaßt werden. Wir machen einen Ansatz als
Produktwellenfunktion:
Spin müssen an
den Hamilton-Operator angepaßt werden. Wir machen einen Ansatz als
Produktwellenfunktion:
Aber der Term ![]() a(r1)
a(r1)![]() a(r2) heißt, daß beide Elektronen am gleichen Kern
sind unabhängig vom Abstand. Dies ist jedoch unwahrscheinlich wegen der
Coulombabstoßung. Ein besserer Ansatz ist deswegen der nach Hatler und
London:
a(r2) heißt, daß beide Elektronen am gleichen Kern
sind unabhängig vom Abstand. Dies ist jedoch unwahrscheinlich wegen der
Coulombabstoßung. Ein besserer Ansatz ist deswegen der nach Hatler und
London:
Durch Einsetzen dieses Ansatzes in die Schrödingergleichung ergeben sich viele Terme. Diese sind aber ähnlich denen des H2+. Daraus folgen die Energieerwartungswerte E = C ±A. C ist wie bei Haa und A ist die Austauschenergie, welche beispielsweise folgende Integrale enthält:
Das Elektron 1 kann von der Wellenfunktion ![]() a* (1) nach
a* (1) nach ![]() b(1) wechseln und das
Elektron 2 von
b(1) wechseln und das
Elektron 2 von ![]() a(2) nach
a(2) nach ![]() b * (2) (gleichzeitiger Austausch). Man erhält die
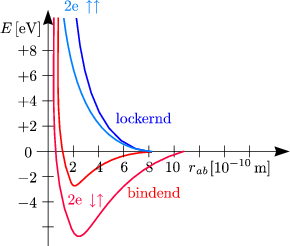
Energie E als Funktion des Abstandes rab:
b * (2) (gleichzeitiger Austausch). Man erhält die
Energie E als Funktion des Abstandes rab:
Bei zwei Elektronen mit ![]()
![]() erhalten wir im bindenden Orbital eine höhere
Bindungsenergie und einen kleineren Abstand.
erhalten wir im bindenden Orbital eine höhere
Bindungsenergie und einen kleineren Abstand.
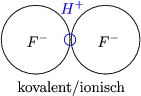
Wir fassen die Hauptmerkmale der kovalenten Bindung zusammen:
Für diese Wellenfunktionen ist die Phasenlage wichtig unter Beachtung des Pauliprinzips.
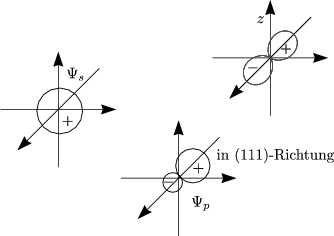
Wichtigstes Beispiel ist die kovalente tetraedrische Bindung bei C, Si, Ge. Betrachten wir beispielsweise das freie Atom von Kohlenstoff näher. Dieses besitzt die Zustände 1s2, 2s2, 2p2 (2px1, 2py2). In der Natur sind die vier gleichwertigen Valenzelektronen pro Atom in tetraedrisch angeordneten sp3-Hybridorbitalen gebunden. Die Wellenfunktion kann somit als Linearkombination geschrieben werden:
Diese sehen ähnlich mit anderem Vorzeichen bei px,y,z aus. Es gibt also vier sp3-Hybridorbitale, die einen Winkel von etwa 109,5o einnehmen.
Betrachten wir beispielsweise einen kubisch flächenzentrierten Kristall, so erkennen wir auch hier die Tetraeder-Struktur:
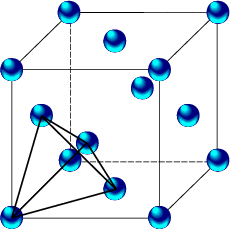
Die Elektronen-Dichte (Valenzelektronen) liegt vor allem zwischen den Ionenrümpfen. Es liegt eine große Bindungsenergie trotz niedriger Koordinationszahl vor.