Diese tritt bei abgeschlossenen Elektronenschalen auf. Wichtig ist sie beispielsweise bei Edelgasen, Molekülen (wie H2) und Polymeren (Kohlenwasserstoff). Dieser Bindungstyp tritt immer auf; er liefert einen kleinen Zusatzbeitrag bei anderen Bindungstypen. Die Van-der-Waals-Wechselwirkung ist eine Dipol-Dipol-Wechselwirkung.
Edelgasatome besitzen kugelförmige Wellenfunktionen. Nichts desto trotz liegen fluktuierende Dipole p1 vor, obwohl <p1> = 0 ist. Aufgrund dieses fluktuierenden Dipols entsteht in dessen Umgebung ein elektrisches Feld. Dieses besitzt folgende Eigenschaft:
Dieses elektrische Feld erzeugt dann in den Nachbaratomen wieder ein
elektrisches Feld, für das p2 = ![]() E (
E (![]()
![]() ) gilt, wobei
) gilt, wobei ![]() die Polarisierbarkeit ist.
Damit gilt:
die Polarisierbarkeit ist.
Damit gilt:
Man benutzt dann folgende Beziehung:
Die Anziehung fällt infolgedessen sehr rasch für gro▀e r ab. Daraus folgt der niedrige Schmelzpunkt. Das Lennard-Jones-Potential ergibt sich nun durch Zusammensetzung von anziehendem und absto▀endem Potential:
Die Potentialformel wird oft so genutzt, wie letztlich angeschrieben.
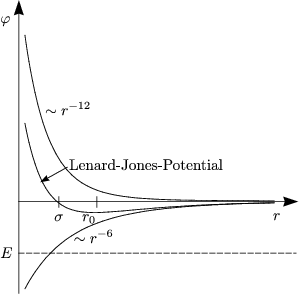
Das Minimum befindet sich bei r0 = 1,12![]() . Wir notieren uns einige
Lennard-Jones-Parameter:
. Wir notieren uns einige
Lennard-Jones-Parameter:
| Element | Ne | Ar | Kr | Xe |
| | 2,74 | 3,4 | 3,65 | 3,98 |
| E [meV] | 3,1 | 10,4 | 14,1 | 20 |
Man kann die Gitterenergie abschätzen, ohne die Nullpunktsenergie zu
berücksichtigen. Das Verfahren ist jedoch sicher ungenau für flüssiges He für
T![]() 0 (fest bei Druck > 2,5MPa). Die Bindungsenergie für ein Atom m ergibt
sich nun durch Summation der Energien bezüglich aller anderen Atome n im
Abstand rmn:
0 (fest bei Druck > 2,5MPa). Die Bindungsenergie für ein Atom m ergibt
sich nun durch Summation der Energien bezüglich aller anderen Atome n im
Abstand rmn:
Der Faktor ![]() kommt daher, weil man alle Energien zweifach summiert. Bei
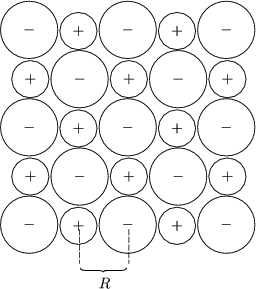
Edelgasen liegt ein kubisch flächenzentriertes Gitter vor:
kommt daher, weil man alle Energien zweifach summiert. Bei
Edelgasen liegt ein kubisch flächenzentriertes Gitter vor:
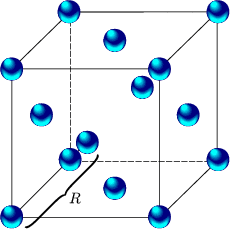
| 12 | Abstand R |
| 6 | Abstand R |
| | |
Damit folgt die Bindungsenergie:
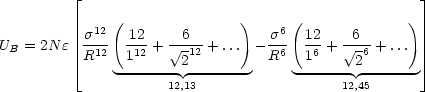
Der Gleichgewichtsabstand R0 erhält man durch Berechnung des Minimums der Wechselwirkungsenergie UB:
Es ergibt sich dann R0 = 1,09![]() und UB(R0) = -8,60N
und UB(R0) = -8,60N![]() .
.
| Element | Ne | Ar | Kr | Xe |
| | 1,15 | 1,11 | 1,09 | 1,09 |
Abweichungen sind erklärbar durch Nullpunktsschwingungen. UB(R0) stimmt gut und sehr gut unter Berücksichtigung der Nullpunktsschwingungen. Siehe hierzu auch Isotopeneffekt:
Eine heteropolare Bindung kann entstehen durch Elektronentransfer wie beispielsweise bei Na+ und Cl-. Infolge der Coulombkräfte entsteht eine ungerichtete Bindung. Für ein Ionenpaar bestehend aus kugelförmigen Ionen wollen wir eine erste Abschätzung vornehmen:
Bei mehreren Nachbarn ist die Energie eher grö▀er. Diese Energie kann man experimentell nur indirekt messen, weil freie Ionen nicht existieren. Hierzu verwendet man einen erdachten Kreisproze▀, nämlich den sogenannten Born-Haber-Kreisproze▀:
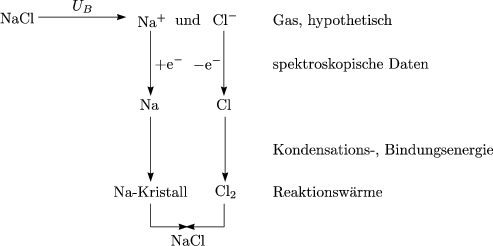
Als Bilanz ergibt sich UB = -8,16eV/Paar. Wir wollen die Bindungsenergie berechnen:
Das Potential für ein Ion m ergibt sich durch:
Der erste Term berücksichtigt die Absto▀ung und der zweite die Coulomb-Wechselwirkung. Berücksichtigen wir nur die Anzahl z der nächsten Nachbarn, so gilt folgende Näherung:
Der zweite Term konvergiert schlecht, wegen der ![]() -Abhängigkeit. Dieses
Problem löst man durch Einführung der Madelungkonstante, in die man alles,
was bei der Summation gefährlich ist, steckt:
-Abhängigkeit. Dieses
Problem löst man durch Einführung der Madelungkonstante, in die man alles,
was bei der Summation gefährlich ist, steckt:
Diese Konstante enthält die Struktur des Festkörpers. Betrachten wir beispielsweise eine lineare Kette:
![]()
In drei Dimensionen liegt nur „bedingte“ Konvergenz vor. Ein besonderes Verfahren ist die Konstruktion einer Evjen-Zelle. Betrachten wir hierzu ein zweidimensionales Beispiel:
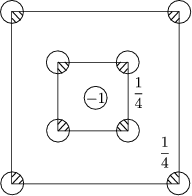
Man konstruiert also ladungsneutrale Zellen. Durch schrittweise Vergrö▀erung
der Ladungsbruchteile ergibt sich eine schnelle Konvergenz. Als Beispiel in drei
Dimensionen betrachten wir CsCl (8 .![]() Ladung). Die Madelungkonstante ist
strukturabhängig.
Ladung). Die Madelungkonstante ist
strukturabhängig.
| NaCl-Struktur | |
| CsCl-Struktur | |
| ZnS-Struktur | |
Für N Ionenpaare ergibt sich:
Die Gleichgewichtslage erhält man wieder durch Nullsetzen der ersten Ableitung:
Damit resultiert:
Den ersten Term bezeichnet man als Madelungsenergie. Der zweite Term ist
ein Korrekturterm (Absto▀ung ![]() 10% bei R0). Für NaCl mit R0 = 2,82┼
folgt:
10% bei R0). Für NaCl mit R0 = 2,82┼
folgt:
Aus der Kompressibilität ergibt sich, da▀ die Absto▀ung bei R = R0 weniger
steil ist als ![]() . Besser ist hier das Born-Mayer-Potential:
. Besser ist hier das Born-Mayer-Potential: