4.1 Punktdefekte

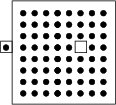
Punktdefekte besitzen atomare Größe. Es kann sich beispielsweise um eine Leerstelle handeln. Fehlt das betreffende Atom irgendwo im Festkörper und befindet sich beispielsweise an der Oberfläche, so spricht man vom Schottky-Effekt. Dieser tritt immer auf; er ist entropiegetrieben.

Die Konzentration dieser Defekte im Gleichgewicht ergibt sich aus dem Minimum der freien Energie:

T und V sei hier fest. Innere Energie U und Entropie S nehmen mit der Zahl N_L zu. Eigentlich müßte man jedoch die freie Enthalpie betrachten (p, T fest):

Diese variiert aber nur schwach, solange V const. gilt. Wegen N_L « N gibt es keine Wechselwirkung zwischen einzelnen Defekten.

Bei der Bildung eines solchen Effekts bekommen wir also einen Beitrag zur inneren Energie:

Daraus resultiert dann auch ein Beitrag zur spezifischen Wärme. E_L sei die Energie zur Erzeugung einer Leerstelle; diese ist jedoch U_B. Es gilt E_L < U_B wegen der Gitterrelaxation. Es gibt zwei Entropiebeiträge:

• Thermische Entropie:

  Diese entsteht durch Veränderung der thermischen Schwingungen des Gitters. Daraus folgt ein weiterer Beitrag:

  

  S_L ist der Entropiezuwachs pro Leerstelle.

• Konfigurationsentropie:

  Dieser Beitrag entspricht der Anzahl der Möglichkeiten N_L Leerstellen auf N + N_L Gitterplätze zu verteilen.

  

Daraus ergibt sich:

Wir müssen nun F_L minimieren:

Mit der Stirling-Formel ln(x!) = xlnx - x für x » 1 erhalten wir:

Damit folgt mit N_L « N:

Und schließlich erhalten wir die Leerstellen-Dichte durch Division durch V :

Typisch ist ~ 5 und E_L ~ 1eV. Dann ergibt sich:

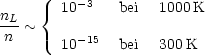
Experimentell bestimmt man dies aus der makroskopischen Längenänderung abzüglich der thermischen Expansion. Durch Auftragen von log über erhält man aus der Steigung E_L < U_B (siehe Übungen). Bei Ionenkristallen gibt es Leerstellenpaare wegen der Ladungsneutralität.

Dies gilt pro Leerstellenpaar. Tatsächlich ist die Zahl viel größer aufgrund der Diffusion.