5.1 Schallausbreitung

Für » a kann man den Festkörper als elastisches Kontinuum auffassen. Den diskreten Aufbau der Materie kann man zunächst vernachlässigen. Man unterscheidet nun:

• Longitudinale Wellen ||
• Transversale Wellen

u ist hierbei die Teilchenauslenkung und der Wellenvektor. Der einfachste Fall ist ein isotroper Festkörper. Diese sind beispielsweise Gläser oder auch Polykristalle mit Korndurchmesser « . Betrachten wir in diesem Zusammenhang die Wellengleichung in x-Richtung, also für die longitudinale Ausbreitung:

ist die Dichte des Materials und C₁₁ das Elastizitätsmodul. Der linke Term beschreibt die „Beschleunigung“ und der rechte die „Kraft“ (=Gradient der Verzerrung ). Für die transversale Wellengleichung folgt:

Das Elastizitätsmodul C₁₁ ist rein longitudinal und C₄₄ ist rein transversal. Bei C₄₄ handelt es sich um das Schermodul G, aber C₁₁ ist nicht gleich dem Elastizitätsmodul E (Young’s Modulus Y; enthält Querkontraktion).

Dieses Modell funktioniert jedoch nicht in anisotropen Kristallen. Man hat hier noch mehr elastische Konstanten, nämlich maximal 21 unabhängige Konstanten bei einem triklinen Material. Bei einem kubischen Material bleiben immerhin noch 3 übrig. Die einfachste Lösung ergibt sich für die Wellengleichung einer monochromatischen ebenen Welle. Wir machen folgenden Ansatz für die Auslenkung u_i, wobei der Index i die Raumrichtung bezeichnet:

Durch Einsetzen erhalten wir die Dispersionsrelation = vq mit:

• Longitudinaler Anteil:

• Transversaler Anteil:

  v_t ist frequenzabhängig wegen dem elastischen Kontinuum.

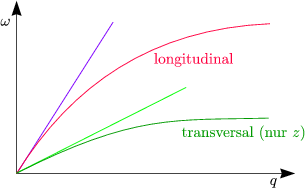
Für große q ändert sich das.

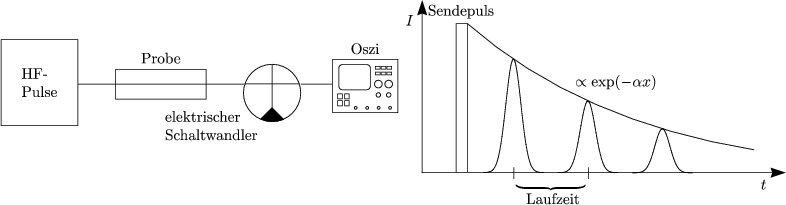
Aus der Schallgeschwindigkeit erhält man dann die elastischen Konstanten.