5.2 Potential und Bewegungsgleichung

Aufgrund der Kopplung der Atome entstehen korrelierte Bewegungen. Es besteht die Tendenz zu kleinen Frequenzen. Wir machen eine harmonische Näherung des Potentials:

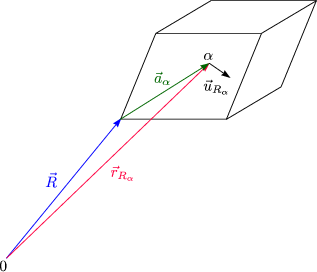
Die potentielle Energie des Gesamtkristalls hängt von der momentanen Lage aller Atome ab. Wir machen für eine Taylorentwicklung um die Gleichgewichtslage.

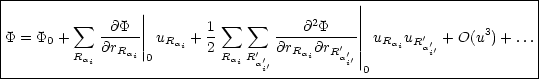
₀ ist die Bindungsenergie. Der erste Term ist gleich Null, da in der Gleichgewichtslage Kräftegleichgewicht herrscht. Der zweite Ausdruck ist der harmonische Term. Zunächst machen wir weiter ohne , ', das heißt wir betrachten nun ein Atom pro Elementarzelle. Wir erkennen die Ähnlichkeit mit dem harmonischen Oszillator:

Hier verwenden wir verallgemeinerte Kraftkonstanten (Krümmung des Potentials):

Damit führen wir den Krafttensor C_R,R' ein:

Die Auslenkung des Atoms bei R' bewirkt eine Kraft auf das Atom bei R. Zur Vereinfachung nutzen wir des weiteren die Translationssymmetrie. C darf also nicht von der absoluten Lage R, R' abhängen, sondern nur von = ' -; wir erhalten damit C. Die Kopplung nimmt mit dem Abstand ab. Deshalb reicht es, für || nur 1 bis 2 Gitterabstände mitzunehmen. Die Bewegungsgleichung (m = F) für das Atom in der Zelle lautet:

Bei Elementarzellen mit r Atomen haben wir 3r = 3N gekoppelte Differentialgleichungen. Die Entkopplung erfolgt durch den Lösungsansatz einer ebenen Welle:

Es muß nicht sein, daß das nächste Atom exakt dieselbe Phase besitzt. enthält damit einen Phasenfaktor, welcher von abhängt. In der Exponentialfunktion ist die Translationsinvarianz enthalten. Es handelt sich um den Spezialfall einer Blochwelle (siehe Elektronen im Festkörper, später).

D_' heißt „Dynamische Matrix“. Es ist die Fouriertransformierte der Kraftkonstanten C und enthält Informationen über elastische Eigenschaften. Wir haben wir ein lineares homogenes Gleichungssystem der Ordnung 3r. Beispielsweise folgt für eine einatomige Basis r = 1 und damit für jedes ein System von 3 Gleichungen für 3 Polarisationen. Die nicht-triviale Lösung erhält man durch Nullsetzen der Determinante der Koeffizientenmatrix:

Für jedes erhalten wir 3r Lösungen ( ), also die Dispersionsbeziehungen. Die Entkopplung des Differentialgleichungssystems hat dazu geführt, daß wir Normalschwingungen berechnen müssen.