[next] [prev] [prev-tail] [tail] [up]

5.3 Gitterschwingungen

5.3.1 Anwendungen auf einfache Beispiele

Wir stellen uns vor, daß eine ein- und zweiatomige Basis vorliegt. Betrachten wir einen eindimensionalen Kristall in Form einer linearen Kette? Lohnen sich solche Betrachtungen jedoch überhaupt? Ja, nämlich für Hauptsymmetrierichtungen.

Ist u ||q , dann kompensieren sich transversale Kräfte zu Null. Wir behandeln nur Kräfte, welche ||u sind, also nu „reine“Moden. Für beliebige Richtungen bezeichnen wir diese als „quasi-longitudinal“ und „quasi-transversal“.

Beispiel:
Betrachten wir also nun einen eindimensionalen Kristall mit einer zweiatomigen Basis. Wir setzen uns im folgenden mit longitudinalen oder transversalen Moden zusammen. Der Determinante der dynamischen Matrix muß gleich Null sein:
| | ||D11 - w2M1 D12 ||= 0 | D21 D22 - w2M2 |

Darin steckt die gesamte „elastische“ Information über die Summe der Nachbaratome.

Beispiel:
Nehmen wir eine einatomige Basis und betrachten also eine „lineare Kette“. Dann fällt der Index a weg und wir erhalten:
2 sum w M = D = s Csexp(iqsa)

Wobei der Gittervektor festgelegt ist durch |h| = s . a, mit der ganzen Zahl s und dem Atomabstand a. Wir schreiben diesen Ausdruck explizit auf:

D = C0 + C1 exp(iqa)+ C- 1exp(- iqa)+ C2 exp(iq2a)+ C- 2exp(- iq2a)+ ...

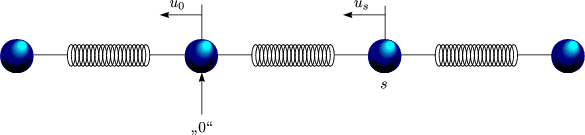
Wir lenken ein bestimmtes Bezugssystem aus: u0. Daraus ergibt sich dan die Rückstellkraft von allen Atomen.

sum F0 oc - u0 ==> C0 = Cs s=0

Lenken wir ein beliebiges Atom aus, so gilt Fs oc us. Daraus ergibt sich dann:

sum sum w2M = C0 - Csexp(iqsa) = Cs(1- exp(iqsa)) s/=0 s/=0

PIC

Außerdem betrachten wir die Translationsinvarianz, also Cs = C-s:

|------ sum -------------------------------- sum ---------------| w2M = Cs (2 - exp(iqsa)- exp(- iqsa)) = 2 Cs(1- cos(qsa))| -------s>0-------------------------------s>0----------------

Nebenbemerkung:
Im Festkörper sind die Reichweiten der Kräfte meist klein.

PIC

Wir werten dies für s = 1 aus, das heißt, nur für den nächsten Nachbarn.

w2 = 2C1-(1 - cos(qa)) = 4C1-sin2(qa-) M M 2

V~ ---| ( ) | w = 2 C1-||sin qa || M 2

Die Auswertung beim nächsten Nachbarn und übernächsten Nachbarn ergibt:

4C1 [ 2(qa) C2 2 ] w2 =-M-- sin -2 + C--sin (qa) 1

Diese Rechnung ist gültig sowohl für longitudinale (s = 1, 2) als auch transversale (s = 1 ok) Polarisation. Aus den experimentellen Dispersionskurven lassen sich die Kraftkonstanten, also auch die interatomaren Potentiale, bestimmen.

5.3.2 Rolle der Brillouinzone

Wir erinnern uns: Die Brillouin-Zone ist die Wigner-Seitz-Zelle des reziproken Gitters. Die Art und Weise, wie man sich das veranschaulichen kann, ist die Phasenbeziehung von benachbarten Atomen:
|---------------------------------------| |us+1 U exp(-ist)exp(iq(s + 1)a) | |-us-= --U-exp(--ist)exp(iqsn)---= exp(iqa)| -----------------------------------------

Der Phasenunterschied nimmt Wert an von 0 bis maximal 2p. Damit ist qa beschränkbar auf den Bereich -p < qa < p. Ohne Beschränkung der Allgemeinheit gilt dann:

p- p- - a < q < a

Was passiert aber für |q'| > p a?

2pm q'= q ± ----, wobei m (- Z a

Addition des reziproken Gittervektors:

us+1 = exp(iq'a) = exp(iqa).exp(±i.2pm) = exp(iqa).1 us

Eine elastische Welle läßt sich zwischen den Atomen damit nicht definieren.

5.3.3 Grenzfall: langwellig q'-->0

2 2 sum q2a2 sum 2 w = M-- Cs (1- cos(qsa)) - ~ -M-- s Cs s>0 s>0

Es gilt w oc q (Schallwellen):

V~ ---- sum 2 w = vq mit vl = C11 mit C11 = s-Cs r s>0a

Für eine kubisch primitiven Festkörper gilt r = Ma2. Damit erhalten wir eine mikroskopische Erklärung für das Elastizitätsmodul. Dies alles geht aus für transversale Wellen; im allgemeinen ist Cs jedoch kleiner, womit (fast immer) V t < V l folgt.

5.3.4 Grenzfall: Grenze der Brillouin-Zone

Wir bilden den Grenzwert q'-->±p a und erhalten:
us+1 us = exp(±if)- 1

Benachbartes Atome sind damit gegenphasig; es liegt also eine stehende Welle vor. Diese entspricht der Bragg-Reflexion einer elastischen Welle am Gitter mit h = 90o.

2asinh = c ==> 2a = c

Ein- und rücklaufende Welle erzeugen damit eine stehende Welle. Dies kann auch mittels der Gruppengeschwindigkeit gezeigt werden:

@w p vgr = @q-'--> 0 f¨ur q '--> a

Die Dispersionskurve wird horizontal bei q = ±p a in Richtungen hoher Symmetrie.

Für eine zweiatomige Basis funktioniert das analog wie bei einer einatomiger Basis. Die Kräfte _L q heben sich auf. Das Differentialgleichungssystem lösen wir mit dem Ansatz, daß die Determinante der Koeffizientenmatrix gleich Null sein muß:

| | ||D11 - w2M1 D12 || | D21 D22 - w2M2 |= 0

An dieser Stelle muß man dann wieder über die Cs nachdenken! Betrachten wir nur die nächsten Nachbarn.

Damit folgt D11 = D22 = C' + C''. As erfährt eine Kraft weg von der Gleichgewichtslage, wenn Bs oder Bs-1 ausgelenkt wird. Wir erhalten also einen negativen Beitrag:

D12 = -(C'+ C''exp(-iqa))

' '' D21 = -(C +C exp(+iqa))

Mit der Abkürzung 2C = C' + C'' erhalten wir:

|| 2C - w2M1 -(C'+ C''exp(-iqa))|| ||- (C'+ C''exp(iqa)) 2C - w2M2 ||= 0

Daraus ergeben sich folgende Eigenwerte:

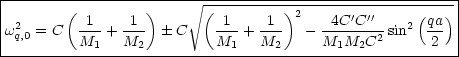
|---------------------------------------------------------| | ( ) V ~ (---------)2------'-''-----(--)-| |w2q,0 = C -1- + -1- ±C -1- + -1- - -4C-C--2 sin2 qa | ----------M1----M2---------M1----M2------M1M2C--------2---|

Man unterscheidet nun:

Der Name „akustisch“ ergibt sich aus der Ähnlichkeit mit Schallwellen; der Name „optisch“daher, falls Ladungen unterschiedlich sind. Es resultiert ein oszillierendes Dipolmoment, womit solche Substanzen infrarot-aktiv sind.

Wir wollen nun außerdem den Grenzfall q'-->pa betrachten mit M1 < M2:

w02 = -2C M1 u2 u1 = 0 nur leichte Atome schwingen
wa2 = 2C- M2 u1 u2 = 0 nur schwere Atome schwingen
w2 = 2C- a M2

Es liegt für wa < w < w0 eine „verbotene Zone“ vor. Die Frequenzlücken in der Dispersion sind überdämpfte Wellen.

5.3.5 Mehratomige Basis

Betrachten wir die verschiedenen Zweige: Liegen p Atome vor, so haben wir 3 akustische Zweige (1 longitudinaler und 2 transversale) und 3p - 3 optische Zweige (1 longitudinaler und 2 transversale).

[next] [prev] [prev-tail] [front] [up]