Die Streuamplitude beträgt:
exp(-i![]() 0t) ist die eingestrahlte Welle,
0t) ist die eingestrahlte Welle, ![]() (
(![]() ) die Streudichte und
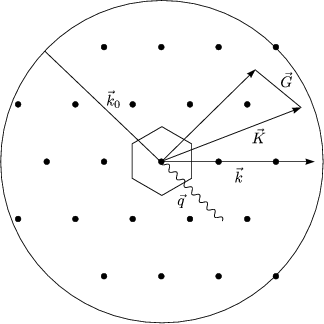
) die Streudichte und ![]() der Streuvektor.
Zur Vereinfachung benutzt man eine einatomige Basis:
der Streuvektor.
Zur Vereinfachung benutzt man eine einatomige Basis:
Daraus ergibt sich dann:
Für kleine uR kann man dies entwickeln:
Daraus ergibt sich dann:
Der erste Summand beschreibt die elastische Streuung und der zweite die
inelastische Streuung. Man summiert dabei über eine sehr große Anzahl von Atomen.
Intensität erhält man nur, wenn ![]() ±
±![]() =
= ![]() . Für die gestreute Strahlung gilt
. Für die gestreute Strahlung gilt
![]() =
= ![]() 0 ±
0 ±![]() +
+ ![]() und
und ![]() =
= ![]() 0 ±
0 ± ![]() q. Wir multiplizieren die Gleichungen mit
q. Wir multiplizieren die Gleichungen mit
![]() :
:
Die erste Gleichung beschreibt Impulserhaltung, die zweite Energieerhaltung. Die
Strahlung (![]() , n, e) erzeugt (-) oder vernichtet (+) ein Quant einer Gitterschwingung.
Quantisierte Gitterschwingungen bezeichnet man als Phononen (
, n, e) erzeugt (-) oder vernichtet (+) ein Quant einer Gitterschwingung.
Quantisierte Gitterschwingungen bezeichnet man als Phononen (![]() ,
,![]()
![]() ) mit dem
Impuls
) mit dem
Impuls ![]() q und der Energie
q und der Energie ![]()
![]() q. Der Impulssatz enthält +
q. Der Impulssatz enthält +![]()
![]() . Es findet damit eine
Erzeugung/Vernichtung eines Phonons statt und gleichzeitig eine Braggreflexion.
. Es findet damit eine
Erzeugung/Vernichtung eines Phonons statt und gleichzeitig eine Braggreflexion. ![]() G
wird an den Kristall an Ganzes übertragen.
G
wird an den Kristall an Ganzes übertragen.
Phononen sind keine lokalisierten Schwingungen eines einzelnen Atoms, sondern jedes ____ Atom im Festkörper nimmt an der Schwingung teil. Der Unterschied zwischen Photon und Phonon ist, daß ein Photon ein fundamentales Teilchen ist, welches einen echten Impuls trägt. Phononen sind kleine fundamentale Teilchen, da sie keinen echten Impuls tragen. Man spricht von Quasiteilchen mit Quasiimpuls.
Für die Energie eines Phonons folgt:
Wir summieren über alle N Atome und erhalten:
Aus der Energie ![]()
![]() erhält man die Auslenkung:
erhält man die Auslenkung:
Betrachtet man Phononen am Rande der Brillouin-Zone, so erhält man mit
![]()
![]() 6Å, V = 6 . 103
6Å, V = 6 . 103 ![]() (Schallgeschwindigkeit) eine Frequenz von
(Schallgeschwindigkeit) eine Frequenz von ![]() = 1013 Hz.
Mit
= 1013 Hz.
Mit ![]() = 7,59
= 7,59![]() und V = 1cm3 ergibt sich dann U = 1,5 . 10-21 cm, was
extrem klein ist! Für
und V = 1cm3 ergibt sich dann U = 1,5 . 10-21 cm, was
extrem klein ist! Für ![]() = 6cm gilt U
= 6cm gilt U ![]() 10-17 cm, was immer noch klein
ist.
10-17 cm, was immer noch klein
ist.
Die Zahl der Phononen bei 300K beträgt typischerweise 1023 ![]() N. Auslenkungen
sind ungeordnet:
N. Auslenkungen
sind ungeordnet:
Der erste Term beschreibt die elastische Streuung, der zweite die Ein-Phonon-Streuung und der dritte die Zwei-Phononen-Streuung. Die Zwei-Phononen-Streuung ist ein Sonderfall aufgrund des Impulsübertrags. Dieser ist beliebig aufteilbar. Es folgt damit ein kontinuierlicher Streuuntergrund.
Die Zahl der Phononen nimmt mit steigender T zu, womit der Untergrund mit T zunimmt. Die Gesamtintensität bleibt erhalten, womit die Intensität der elastischen Peaks abnimmt (siehe Kapitel II):
Für hohe T gilt B ![]() T.
T.