[next] [prev] [prev-tail] [tail] [up]

5.5 Phononspektroskopie

Die Phononenergie beträgt ~~ 10-2 eV (einige THz). Für inelastische Streuung betrachten wir:

dE wq -E- = w-- 0

Für Röntgenquanten beträgt dieses Verhältnis ~~ 10-6 und für thermische Neutronen 10-1.

Inelastische Neutronenstreuung: 3-Achsen-Spektrometer
PIC
Beispiel: Experimentelle Dispersionskurven w(q)
Betrachten wir beispielsweise Kupfer. Dieses besitzt eine fcc-Struktur und eine einatomige Basis. Es existieren nur 3 akustische Phononen (1 mal longitudinal, 2 mal transversal)

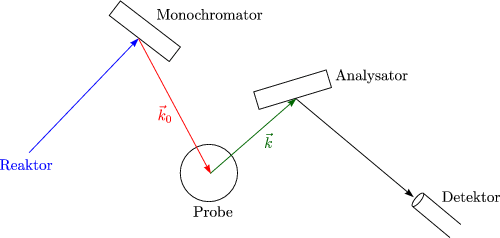
Für [100]-, [111]-Richtung sind die transversal polarisierten Zweige entartet. Für [110] ergibt sich eine Aufspaltung und damit einen Hinweis auf die Wechselwirkung mit den nächsten Nachbarn. Ursache: Für [110] verlasse Brillouin-Zone an einer Kante_____

Betrachten wir außerdem eine fcc-Struktur mit zweiatomiger Basis. aus Li+ und F-. Es ergeben sich drei akustische und 3 optische Zweige. Aufgrund des großen Dipolmoments liegt Infrarot-Absorption vor. Die Zweige sind „überall“ wegen langweitiger Coulomb-Wechselwirkung. Vergleiche dies mit einen kubischen Kristall mit rein „elastischer“ Wechselwirkung. Dann sind die optischen Zweige bei G alle entartet.

5.5.1 Inelastische Lichtstreuung

Für Untersuchung nach G-Punkt
Wellenzahlen: k = k0± q+ G

Für sichtbares Licht beträgt k0 etwa 107 1- m und G ist etwa 1010 -1 m. Daraus ergibt sich G = 0; der Vorgang muß ohne G-Beteiligung stattfinden.

5.5.2 Rayleigh-Streuung

Wie betrachten Streuprozesse ohne Frequenzverschiebung und ohne Phononenbeteiligung, also hq = o: Dann gilt k = j0 für elastische Streuung und es findet eine „Vorwärts“-Streuung im perfekten Kristall statt. „Unsichtbares“ Licht ist nur etwas langsamer aufgrund der Dielektrizitätskonstante; für das Streulicht gilt |k| = |k0|. Es kommt zu keiner „Seitwärts“-Streuung.

In einem realen Kristall ist dies jedoch anders:

Das heißt, es existiert keine totale Translationssymmetrie.

[next] [prev] [prev-tail] [front] [up]