5.7 Spezifische Wrme des Gitters

5.7 Spezifische Wärme des Gitters

Die spezifische Wärme beim konstantem Volumen ist definiert durch:

( ) CV = @U- @T V

U ist hierbei die innere Energie. Experimentell zugänglich ist jedoch oft nicht C_V, sondern C_p. Hierbei gilt folgender Zusammenhang:

2 - 1 Cp- CV = 9b V Tk

ist hierbei der lineare thermische Ausdehnungskoeffizient und das Kompressionsmodul. Bei idealen Gasen der Stoffmenge 1mol gilt C_p - C_V = R. Beim Festkörper gilt jedoch C_p - C_V 0, weil sehr klein (in harmonischer Näherung) ist. Nach der Regel von Dulong-Petit hat ein Festkörper bei hohen Temperaturen den Wert:

J 3R = 3NAkB ~~ 25K-.mol

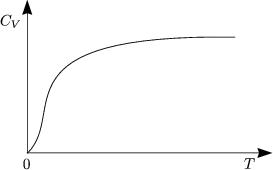
Für tiefe Temperaturen ergibt sich ein rascher Abfall, welcher klassisch jedoch nicht erklärbar ist.

5.7.1 Einstein-Theorie (1907)

Die Theorie ist, das ein Festkörper aus einzelnen unabhängigen identische harmonischen Oszillatoren aufgebaut ist. Deren Energie beträgt:

( ) 1 E = n+ 2 hwE

Man bezeichnet _E als Einstein-Frequenz. Bei hohen Temperaturen ist deren Anteil etwa 3k_B. Die thermische Besetzung „liefert“ den Abfall bei tiefen Temperaturen. Es ergibt sich aber bei der Einstein-Theorie ein zu schneller Abfall. Diesen Unterschied bekommt man besser in den Griff, indem man gekoppelte Bewegungen von Oszillatoren (Gitterdynamik) berücksichtigt. Eben diese Gitterdynamik spielt eine große Rolle bei kleinen Frequenzen. Damit erhält man einen etwas größeren Wert für C_V als bei Einstein, aber dennoch diesen raschen Abfall. Das Vorgehen ist folgendes. Man betrachtet die Zustandsdichte der Phononen:

Deren Energie
Thermische Besetzung

Daraus erhält man die innere Energie und somit die spezifische Wärme. Ist die Phononenzustandsdichte eigentlich kontinuierlich? NEIN! Wir betrachten die Eigenmoden bzw. Nomalschwingungen des gesamten Festkörpers. Hierbei gibt es zwei Abzählmethoden:

Feste Randbedingungen (offenes, festes Ende) $c 2c 3c --,--, --, ...103Obert¨one 2 2 2$
Hier: Periodische Randbedingungen
Wir schauen uns einen endlichen Kristall (Parallelepiped) an, welcher periodisch im dreidimensionalen Raum fortgesetzt wird. Das Phononenspektrum ist diskret aber im allgemeinen sehr dichte und daher quasi kontinuierlich. Die Gesamtzahl der Zustände beträgt 3N.
Wir betrachten als einfachsten Fall einen Würfel der Kantenlänge L. Die Auslenkung der Atome ist periodisch mit L.
$u(x,y,z,t) = u(x + L,y,z,t) = u(x,y + L,z,t) = u(x,y,z + L,t)$
Wir verwenden den Ansatz einer ebenen Welle:
$u(r,t) = U exp[i(qr - wqt)]$
Beispielsweise gilt für die x-Richtung:
$exp(iqr) = exp[i(q(x+ L,y,z))] = exp(iqr).exp(iqx .L)$
Der letzte Term muß nun aufgrund der Periodizität gleich 1 sein: exp(iq_xL) 1. Damit erhält man die erlaubten Wellenzahlen:
$2p- 2p- 2p- qx = L nx, qy = L ny, qz = L nz$
n_i sind dabei ganze Zahlen, also 0, ±1, ±2, ±3, .... Für jeden Phononenzweig haben wir maximal 3pN' = 3N, wobei p die Anzahl der Atome pro Elementarzelle ist und N' die Anzahl der Elementarzellen. Daraus ergeben sich n Werte für die Quantenzahlen der Phononen:
$N 13 N 13 - --- < nx,y,z < --- 2 2$
Im allgemeinen ist die Elementarzelle nicht kubisch, sondern es handelt sich um ein Parallelepiped mit Kantenlängen je in Richtung der Basisvektoren ₁, ₂, ₃. Daraus erhalten wir dann:
$[ 3 V~ --- ] exp i N 'q(a1 + a2 + a3) =_ 1$
Wir zerlegen die nach Basisvektoren des reziproken Gitters, also ₁, ₂ und ₃. Daraus erhalten wir:
$sum nigi qi V~ -' i N$

$|nmax|= 1 V~ 3N-'qmax = ±1 g i 2 i 2 i$
Wir erhalten die Dichte im q-Raum als:
$r = -N'-= ----N'-----= -V--- q VBZ g1 .(g2 × g3) (2p)3$
Dieses ist homogen und quasi kontinuierlich. Die minimale Zustandsdichte D() folgt durch die Zahl der Zustände zwischen _q = const. und _q + d_q = const..
$integral -V--- 3 D(w) dw = (2p)3 d q w=const.$
Der Vorfaktor ist die Dichte im q-Raum und d³q ein Volumenelement im q-Raum.

dS_n ist das Flächenelement auf = const. und dq ist der Abstand zur Fläche + d = const.. Mit d = |grad_q _q|dq gilt dann:
$d3q =---dSw---dw |gradq w _L |$
Damit erhalten wir D():
$V integral dSw ||dw|| D(w) = 8p3 vgr-mit vgr = ||dq||= |gradqwq| w=const.$
D() ist groß bei flacher Dispersion. Bei v_g = 0 spricht von der Van-Horc-Singularität.
5.7.2 Debye-Näherung
Diese ist analytisch rechenbar. Historisch:
- Isotroper Festkörper mit einatomiger Basis
  Dann erhält man nur akustische Phononen.
- Dispersion = vq elastisches Kontinuum
  _q = const. ist eine Kugel!
$integral dS = 4pq2 w$
Für den Zweig i, wobei i für „longitudinal“ oder „transversal“ steht, erhalten wir dann:
$-V-4pq2 -V- w2- Di(w) = 2p3 vi = 2p2 v3i$
Für die Debye-Zustandsdichte resultiert:
$V ( 1 2 ) 3V w2 D(w) = 2p2 v3 + v3 w2 - ~ 2p2v3- oc w2 l t D$
Hierbei wurde kein Unterschied mehr zwischen v_l und v_t gemacht. Die Abschneidefrequenz _D liegt so, daß:
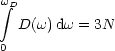
$w integral D D(w) dw = 3N 0$

$|-------------| |w = VD-3 V~ 6p2 | --D----a------|$
_D ist die sogenannte Debye-Frequenz.
Weiteres Vorgehen:
- Betrachte die thermische Energie eines harmonischen Oszillators
  Daraus ergibt sich die Besetzungszahl:
  $-----1------- <n> = exp (-hw) - 1 kBT$
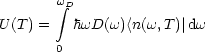
- Berechnung der inneren Energie aus: $w integral D U (T ) = hwD(w) <n(w,T)|dw 0$
  Bei diesem Ansatz wird die Nullpunktsenergie weggelassen, da diese Konstante bei der Ableitung sowieso keine Rolle mehr spielt.
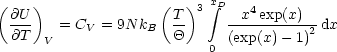
- Debye: Spezifische Wärme: $x (@U ) (T )3 integral D x4 exp(x) -@T = CV = 9NkB Q- (exp(x)--1)2 dx V 0$
  ist ein materialspezifischer Parameter, welcher als Debye-Temperatur bezeichnet wird.
  $kBQ = hwD$

5.7.3 Thermische Besetzung eines harmonischen Oszillators

Die Energieeigenwerte des harmonischen Oszillators im Gleichgewicht sind:

( ) E = n+ 1 hw n 2

n + ist nicht fest! Die Besetzungswahrscheinlichkeit P_n ergibt sich nun mittels des Boltzmann-Faktors:

( ) Pn oc exp --Ea- kBT

Wie der Vorfaktor aussieht, hängt von der Normierung ab. Wir normieren die Summe der Wahrscheinlichkeiten auf 1:

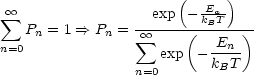
( ) sum oo exp -kEBaT- Pn = 1 ==> Pn = sum oo --(------)- n=0 exp - En-- n=0 kBT

( -nhw)[ ( hw--)] Pn = exp -kBT 1- exp - kBT

Die mittlere Energie des harmonischen Oszillators ergibt sich aus:

oo sum [ ( hw )] oo sum ( 1)[ ( hw )]n E(w,T) = EnPn = 1- exp - k-T- hw n + 2 exp -k--T n=0 B n=0 B

Mit _nnxⁿ = x _nxⁿ = ergibt sich schließlich der Erwartungswert der Energie:

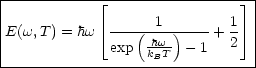
|----------- |_ ---------------- _| | | | |E(w,T ) = hw |_ --(--1-)----+ 1 _| | | exp khBwT- - 1 2 | --------------------------------

Vergleiche dies mit E_n = :

<n> = ---(-1-)----- exp -hw- - 1 kBT

Es handelt sich hierbei um den Erwartungswert der Quantenzahl N oder auch anders gesagt um die mittlere Besetzungszahl eines Phononenzustandes, den man mit und bezeichnen kann. Diese Bose-Einstein-Statistik gilt übrigens auch für Photonen. Die innere Energie erhält man nun durch Multiplikation mit der Zustandsdichte und Integration:

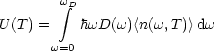
w integral D U(T) = hwD(w)<n(w,T )>dw w=0

Hierbei wurde die Nullpunktsenergie als irrelevante Konstante weggelassen. Durch Einsetzen der Zustandsdichte und Besetzungszahl folgt:

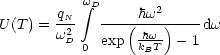
qN integral wD hw2 U (T ) = w2 ---(-hw-)----dw D 0 exp kBT - 1

Mit der Debye-Temperatur k_B = _D, x = und x_D = erhält man nun:

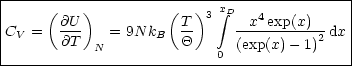
|-------------------------------------------| | ( ) ( )3 x integral D 4 | |CV = @U- = 9N kB T- -x--exp(x)-2 dx| | @T N Q 0 (exp(x)- 1) | ---------------------------------------------

Wir haben hier einen Materialparameter, nämlich die Debye-Temperatur ; ansonsten ist die Formel jedoch universell. Man bezeichnet die Beziehung auch als Debye’s spezifische Wärme ______________________.

Grenzfälle:

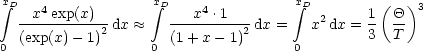
Hohe Temperaturen: T, x0: $integral xD x4exp(x) integral xD x4 .1 integral xD 1(Q )3 ----------2-dx ~~ ---------2 dx = x2dx = - -- 0 (exp(x) - 1) 0 (1+ x- 1) 0 3 T$
Daraus ergibt sich dann C_V = 3N_Ak_B = 3R nach der Dulong-Petitschen Regel.
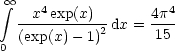
Tiefe Temperaturen: T0, x_D $oo integral x4exp(x) 4p4 (exp(x)--1)2 dx =-15- 0$

$( ) 12p4 T- 3 3 CV = 5 NkB Q oc T$

Beispiele für Debye-Temperaturen:


Element	C	Si	Fe	Al	NaCl	Au	Ar	He (fest)

[K]	2200	640	470	430	320	164	92	25

Bei ~ v_D ergibt sich eine Variation von etwa zwei Größenordnungen und damit bei C_V eine Variation um ungefähr sechs Größenordnungen. Die Debye-Näherung ist sehr gut bei T < und bei T > . Im mittleren Bereich ist das Spektrum der Gitterschwingungen wichtig, womit es Abweichungen von Debye’s spezifischer Wärme gibt.

Oft besser ist es, akustische Phononen durch Debye’s Näherung und optische Phononen durch Einsteinoszillatoren. Für die spezifische Wärme mehrdimensionaler Systeme gilt:

D() ²: Dreidimensional (Kugelschale)
D() : Zweidimensional (Kreisringe)
D() ⁰: Eindimensional

Allgemein gilt für die Zustandsdichte D() ^d-1. Und damit gilt C_V T^d.

Betrachten wir beispielsweise ³He-Atome auf Graphit (zweidimensional): variiert hier in Abhängigkeit vom Bedeckungsgrad von etwa 18K bis 34K von 0,08 bis 0,09.

[next] [prev] [prev-tail] [front] [up]

5.7 Spezifische Wärme des Gitters

5.7.1 Einstein-Theorie (1907)

5.7.2 Debye-Näherung

Weiteres Vorgehen:

5.7.3 Thermische Besetzung eines harmonischen Oszillators

Grenzfälle:

Beispiele für Debye-Temperaturen: