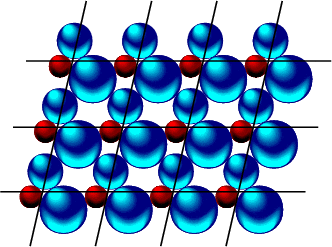
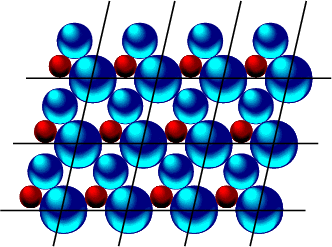
Die regelmäßige Form von Kristallen steht in direktem Zusammenhang mit der regelmäßigen Anordnung identischer Bausteine. Bewiesen wurde diese Zusammenhang im Jahre 1912 von Laue, Friedrich und Knipping durch Beugungsexperimente mit Röntgenlicht (Kapitel 2, Periodizität, Translationsgitter).
Ein Idealkristall ist eine dreidimensionale, unendlich große periodische Anordnung identischer, gleichorientierter Struktureinheiten.
Es handelt sich um die strukturelle atomare Untereinheit, die jedem Gitterpunkt/Parallelepiped zugeordnet ist.
Gitter und Basis bilden die sogenannte Kristallstruktur.
Eine systematische Beschreibung erfordert das Erkennen von allen Symmetrieeigenschaften
durch sogenannte Symmetrieoperationen (
Kristall in sich selbst überführen). Man
kann damit die Kristallstruktur klassifizieren. Wenn man dies vollständig durchführt,
benötigt man die sogenannte Gruppentheorie. Die wichtigsten Operationen seien
aufgelistet:
Wenn man von einen gewählten Punkt genau eine Periode weitergeht, muß die Umgebung wieder gleich aussehen.
Hierbei wird mindestens ein Raumpunkt festgehalten; man führt beispielsweise Spiegelungen oder Drehungen durch.
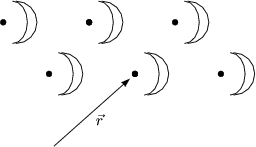
Die Umgebung U(
) eines bestimmten Punktes ist identisch nach Verschiebung um
einen Gittervektor (Translationsvektor) 
.
, 
und 
sind die Basisvektoren des Punktgitters oder auch Raumgitters. Diese
Basisvektoren spannen das Parallelepiped auf (periodisch, raumfüllend). Die Wahl
eines solchen Parallelepipeds ist nicht eindeutig. Mit der Wahl einer sogenannten
Elementarzelle____________ durch 
, 
und 
läßt sich die Struktur beschreiben. Eine
solche Elementarzelle heißt primitiv, wenn ein einziger Gitterpunkt und eine
Struktureinheit enthalten ist. Mit einer nicht primitiven Zelle sind nicht alle
Gitterpunkte erreichbar. Manchmal ist diese aber trotzdem nützlich, um Symmetrien
aufzuzeigen.
, 
'
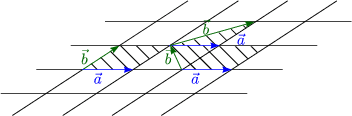
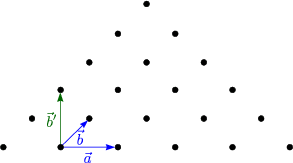
sind nicht primitiv; 
ist durch Linearkombination nie erreichbar.