, 
und 
bekannt. Bei amorphen Festkörpern benötigte man jedoch eine Liste von
1020 Einträgen, um die Atompositionen anzugeben. Deshalb sind hier zur
Beschreibung der Struktur statistische Methoden notwendig. Dafür gibt es gewisse
Voraussetzungen:
In einem Kristall sind alle Atompositionen durch die Translationsvektoren , und
bekannt. Bei amorphen Festkörpern benötigte man jedoch eine Liste von
1020 Einträgen, um die Atompositionen anzugeben. Deshalb sind hier zur
Beschreibung der Struktur statistische Methoden notwendig. Dafür gibt es gewisse
Voraussetzungen:
Elektrische Eigenschaften usw. sind invariant gegenüber Drehungen.
Wichtig ist außerdem die ortsabhängige Teilchenzahldichte n(
). Es handelt sich um die
Wahrscheinlichkeit, ein Teilchen im Volumenelement d3x anzutreffen. Der Term
n(
)d3x ist die Zahl der Teilchen, die sich im Volumenelement d3x am Ort 
befinden. Die gröbste, einfachste Beschreibung der Teilchenzahldichte erhalten wir
durch:
Es handelt sich hierbei um die mittlere Teilchendichte. Diese ist bei amorphen
Festkörpern etwa 1% bis 10% kleiner als in Kristallen. Die ideale Abweichung wollen
wir nun durch die Paarkorrelations-/Zweiteilchenkorrelationsfunktion beschreiben. Es
ist ein Vergleich mit Modellrechnungen und Beugungsexperimenten möglich. Wir
nehmen nun an, daß nur eine einzige Teilchensorte vorliegt und fragen nach der
Wahrscheinlichkeit für Teilchenmittelpunkt am Ort 
' im Volumen d3x', wenn
gleichzeitig am Ort 
im d3x schon ein anderes ist, wobei es nicht auf den Ort 
,
sondern auf den Verschiebungsvektor 
= 
'-
(relative Lage der beiden Teilchen)
ankommt.
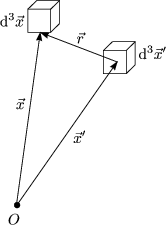
Die kann jetzt mit Hilfe der Teilchenzahldichte annähern. Die Wahrscheinlichkeit, ein
Teilchen in d3x zu finden ist proportional zu n(
)d3x. Das Teilchen gleichzeitig in
d3x' bei x' zu finden, ist proportional zu n(
)n(
-
)d3xd3x'. Jetzt betrachten wir
nicht ein bestimmtes d3x bei 
, sondern irgendein Volumenelement in v. Die
Wahrscheinlichkeit ist dann proportional zum Integral
Wir betrachten nun die dimensionslose Größe mit dem Erwartungswert
<n(
)n(
+ 
)>:
Man nennt diese Größe Paarkorrelationsfunktion; sie ist definitionsgemäß gleich Null
für 
= 0.
Ein wichtiger Parameter ist nun:
Diese Größe charakterisiert den Zwischenraum pro Teilchen. Wir haben zwei Grenzfälle:
Das heißt, es könnte sich um ein verdünntes Gas handeln.
Den allgemeinen Fall findet man analysiert im ZERUKE und PRINZ Festkörperphysik 41, 184 (1927).
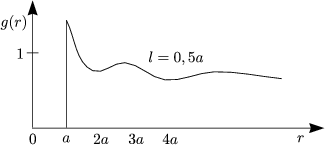
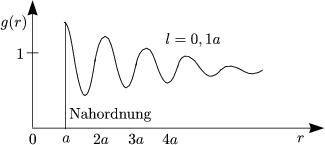
Hierbei handelt es sich um Oszillationen. Dies entspricht einer lokalen Ordnung (Nahordnung). In drei Dimensionen funktioniert dies ähnlich:
